一种辐射型配电网潮流的改进算法

陈小明

（广东电网公司韶关供电局，广东 韶关 512028）

在进行配电网的潮流计算时，会因为收敛性的问题，一些经典的潮流算法，不能直接应用于配电网的潮流分析计算。有两个最重要的原因造成了这种情况：一是配电网各条支路较之输电网具有较高的电阻电抗比，即配电网支路的R/X较高；二是配电网通常具有的辐射型网络结构，仅有一个电源节点，除干线外还有较多的支线。

文献[1]在Augugliaro等人的研究基础上，通过简单的编号方法和两次的矩阵变换得到了一种辐射型配电网的结构矩阵。本文在此基础上提出了一种简单的支路计算顺序矩阵，并利用此计算顺序矩阵引导整个配电网潮流的迭代计算过程。将这种改进算法运用于原文中给出的12节点，33节点和69节点的配电网进行潮流计算后，通过计算结果可以看出，支路计算顺序矩阵的引入不仅可使迭代次数减少 3/4以上，同时也提高了计算结果的精度，在保证相同计算精度的情况下，也可以减少迭代时间，使这种基于配电网结构的算法得到了极大的改进，具有更好的适应性。

1 配电网结构矩阵及支路计算顺序矩阵

1.1 构造配电网结构矩阵

[1]中提出了一种简单的辐射型配电网的编号方法，应用这种编号方法，可以得到一个直接反映辐射型配电网结构的矩阵 S，以及一个用于控制累加次数的矩阵N。

对图1所示配电网，应用文献[1]给出的编号方法，可以得到该配电网的结构矩阵S1和累加次数控制矩阵N1。

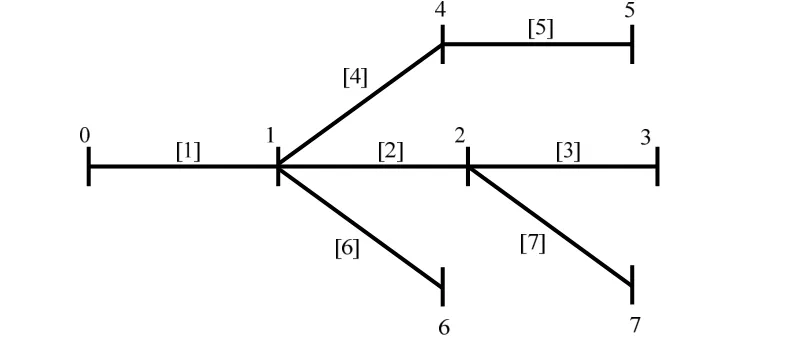
图1 一个简单的辐射型配电网

这种编号方法得到的两个矩阵有如下的特点：

1）辐射型配电网的支路编号和支路末端节点的编号相同。

2）结构矩阵S的行号与配电网的支路编号形成一一对应的关系（S的第i行对应配电网的支路i），支路i后所含节点的编号对应S矩阵第i行的各个非0元素，支路i后所包含的支路的编号对应S矩阵第i行第2列开始的各个非0元素。

3）N的行号对应支路编号，数值表明了各支路后包含的节点数。

1.2 构造配电网支路计算顺序矩阵

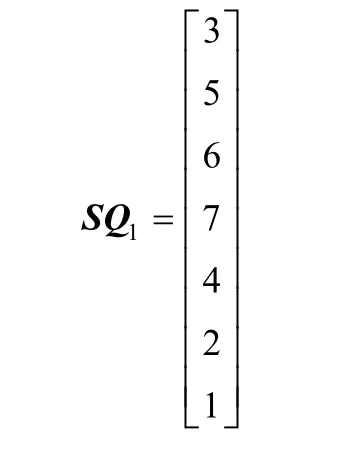
本文在文献[1]所给的编号方法以及配电网结构矩阵的基础上再引入一个支路计算顺序矩阵SQ。利用矩阵 S，将各条支路按照支路后节点数由少到多，以及支路编号由小到大排序就可以得到矩阵SQ。按上面给出的排序规律可以得到图1所示配电网的支路计算顺序 SQ1。支路计算顺序矩阵直接决定了在进行回代计算时，所有支路的计算顺序，比起逐条支路拆除的方法更加简单，这种方法的实质是先完成所有末端支路的损耗计算，再按支路后节点的个数的由少到多逐条完成所有支路损耗的计算，从而保证了支路损耗计算顺序的正确性。

2 配电网潮流计算原理

2.1 配电网潮流计算的前提条件

辐射型配电网的潮流计算模型由图2给出。

2.2 配电网潮流计算的步骤

步骤1：回代计算支路损耗

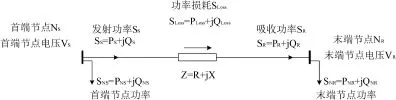
图2 辐射型配网潮流计算模型

支路损耗计算为回代法，由末端支路开始往前计算，各支路的回代计算顺序由计算顺序矩阵 SQ决定。末端支路的吸收功率等于末端节点功率，即故末端支路的损耗可以直接按式（1）和式（2）求得。

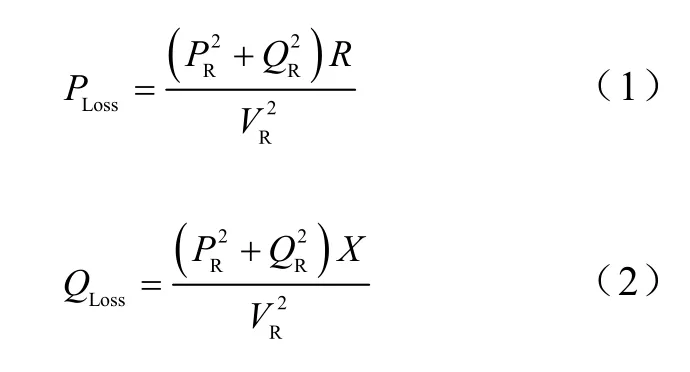
若支路为非末端支路，应先按式（3）、式（4）求得其支路末端的吸收功率，式中的i为支路编号，计算顺序由SQ（i）决定，用矩阵N控制累加次数，用S找到支路i后所包含的节点和支路。之后再用式（1）和式（2）求得非末端支路的损耗。

步骤2：回代计算支路首端发射功率

各条支路的首端发射功率可按式（5）和式（6）求得。

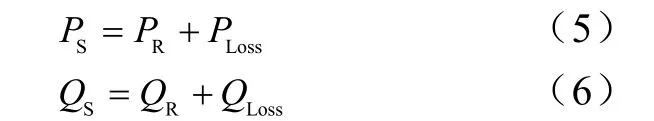
步骤3：前推计算各节点电压幅值

通过式（7）和式（8）求得电压幅值修正量的纵分量和横分量。再利用式（9）求得修正后的节点电压幅值。该计算为前推计算，计算顺序为节点的编号顺序。

步骤4：判断是否满足迭代停止条件

当完成一轮回代前推计算以后，若各节点迭代前后电压幅值之差的最大值小于设定的收敛条件，则认为迭代已满足计算精度要求，迭代停止，进入步骤5，否则转回步骤1，开始下一轮迭代。

步骤5：求取各个节点的电压相角

完成迭代计算后，利用式（10）和最终的节点电压幅值计算结果，求得各个节点电压的相角。求节点的电压相角时，从电源节点开始，DV和dV保留的是最后一次迭代计算的结果。

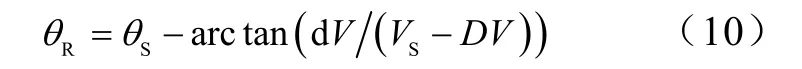
3 仿真计算及结果分析

3.1 在配电网中运用潮流算法进行仿真计算

将上述的算法用Matlab语言完成编程，并利用文献[1]中提供的12节点，33节点和69节点配电网数据进行了测试，测试的环境为Matlab 7，Intel i5 CPU，Windows 7，RAM 4G。12节点配电网的测试结果列于表1中。

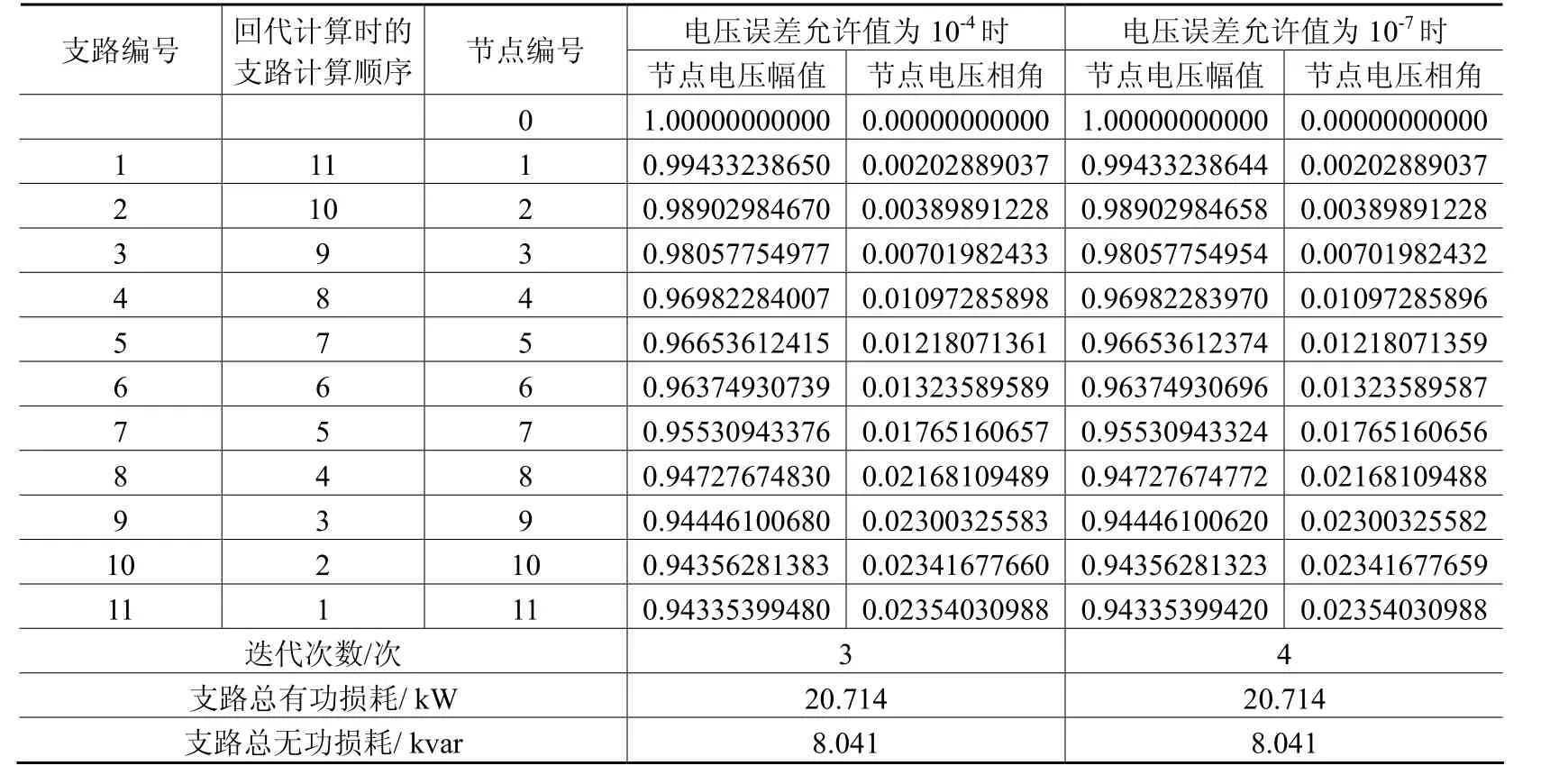
表1 12节点配电网测试结果

3.2 仿真计算结果分析

文献[1]的算法和改进结果算法的对比结果列于表2。

表2 配电网测试结果对比

从表2中可以看出，在引入了一个支路计算顺序矩阵之后，在10-4迭代计算精度控制下，12节点、33节点、69节点测试配电网迭代计算的次数均为3次，对比文献[1]中的13次、19次和25次迭代次数有了极大的改善。

将改进算法应用于12节点、33节点、69节点测试配电网，在10-4和10-7两种精度控制下得到的节点电压幅值结果之差的最大值分别为 6.0×10-10，1.9×10-7，3.4×10-7，迭代次数之差为1次、2次、2次，故支路计算顺序矩阵的引入，使得迭代计算在10-4精度控制下就已经能够得到非常接近于10-7精度控制下的计算结果了，可以利用此特性减少计算时的迭代次数，减少迭代时间的同时，得到一个非常精确的结果。

在相同精度的控制下，12节点、33节点、69节点潮流算法所需时间较原算法也有了一定程度的改善。

4 结论

在进行辐射型配电网的潮流计算的计算时，由于需要面对配电网日益庞大的规模以及满足供电可靠性的需求，使得对辐射型配电网潮流计算方法的速度和精度要求越来越高。而配电网本身固有的特殊性也使得配电网潮流计算的算法有着其自身的特点。本文提出了一种结合辐射型配电网特殊编号方法的配电潮流算法的改进算法，利用该算法中配电网节点和支路编号的特殊性，设定了一个简单的支路计算顺序矩阵，在回代计算时利用此矩阵规定的计算顺序完成各条支路功率损耗的计算，在不改变原编号方法和相应算法的基础上，可以在极大地降低原算法迭代次数的同时取得一个高精度的计算结果，使这种算法具备了更好的实用性，能得到更广的应用。

参考文献

[1]HAMOUDA A, ZEHAR K.Efficient Load Flow Method for Radial Distribution Feeders[J].Journal of Applied Sciences,2006,6(13):2741-2748.

[2]ASHOKKUMAR R, ARAVINDHABABU P. An Improved Power flow Technique for Distribution Systems[J].Journal of Computer Science,Informatics & Electrical Engineering, 2009,1(30).

[3]ARAVINDHABABU P, ASHOKKUMAR R. A Fast Decoupled Power Flow for Distribution Systems[J].Electric Power Components and Systems,2008,36:932-940.

[4]何仰赞,温增银.电力系统分析[M].武汉：华中科技大学出版社,2002.

[5]KOTHARI D P, NAGRATH I J.现代电力系统分析[M].北京:清华大学出版社,2009.

[6]龚纯,王正林.MATLAB语言常用算法程序集[M].北京：电子工业出版社,2008.

[7]LIN W M, TENG J H. Three-phase Distribution Network Fast-decoupled Power Flow Solutions[J]. International Journal of Electrical Power and Energy Systems, 2000,22(5):375-380.

[8]SHIRMOHAMMADI D, HONG H W, SEMLYEN A,LUO G X. A compensation-based power flow for weakly meshed distribution and transmission networks[J]. IEEE Trans, 1988,PWRS-3:753-62.