基于小波变换的电力系统谐波分析研究

谷文静 金 涛

（福州大学电气工程与自动化学院，福州 350108）

随着电力电子技术的发展，供电系统中增加了大量的非线性负载，特别是以开关方式工作的静止变流器，从低压小容量家用电器到高压大容量的工业交、直流变换装置都有着广泛的应用，它是一种非线性时变拓扑负荷，不可避免地会产生非正弦波形，向电网注入谐波，已成为电网的“公害”[1]。

通过对电网谐波的研究和治理，可以更有效地提高谐波检测分析的精度和速度，为谐波源追踪、谐波的治理、电力系统谐波的规范管理提供依据，对提高电网的供电质量、保证电力系统、供电系统和电力用户的安全经济运行，具有重大意义。电力系统谐波检测主要是通过谐波电流的测量来实现，它主要有以下几种方法：①采用模拟带通或带阻滤波器检测；②卡尔曼滤波器检测；③基于瞬时无功功率的谐波检测；④基于傅里叶变换的谐波检测；⑤基于神经网络的谐波检测；⑥基于小波变换的谐波检测[2]，神经网络理论和小波分析方法应用于谐波测量是目前正在致力研究的新方法和新理论，它可以提高谐波测量的实时性和精度。本文简要阐述了谐波的产生原因，并在此基础上对基于小波变换的电网谐波进行了检测分析，根据分析与仿真的结果，利用无源滤波器对谐波进行了有效治理。

1 谐波产生原因分析

电网谐波来自于3个方面：①发电质量不高产生的谐波；②输配电系统产生的谐波；③用电设备产生的谐波。由于电网电压的偏移一般都在±7%以下，所以发电和变电设备所产生的谐波分量实际上都比较小，比国标GB/T 14549-93《电能质量公用电网谐波》的考核标准低的多，因此发电和变电设备产生的谐波不是影响电网电能质量的主要因素，而非线性用电设备是电网的主要谐波源。

在供电系统中，当理论上电网供电的正弦基波电压加在非线性负荷上时，负荷吸收的电流与施加的波形不同，畸变的电流将在电源系统的阻抗上产生电压降，因而产生畸变电压。而变电压降对所有用电负荷（线性和非线性）产生影响，产生更多畸变电压，如图1所示。在配电系统中，某种比例电抗器组或系统自身电抗与电容比率合适时，将会对某种特定次数的谐波电流产生谐振放大，有时可达谐波源电流的 10倍以上。

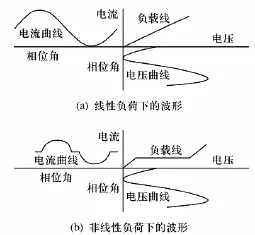
图1 线性和非线性负载下的波形图

随着分布式电源的不断应用，供电公司也加入了电流谐波源的行列，各种形式的能量，如光能、风能、天然气甚至氢燃料都用来满足未来的电力需求。在电力需求高峰期，大量的谐波产生单元加入到为供电公司提供电能得分布式发电机中。

2 小波分析在谐波分析中的应用

小波变换是一种时域处理的技术，广泛应用于对时变信号的处理中。它具有分析频率降低时视野自动放宽的特点，并且也具有品质因数恒定的特点[3]。所谓小波，简单地说就是一个满足条件的函数ψ通过伸缩平移而产生的一个函数簇。

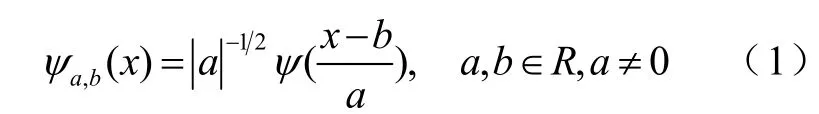
对于任意的 f ∈L2( R)，若φ∈ L2( R)，则 f ( t)的连续小波变换定义为

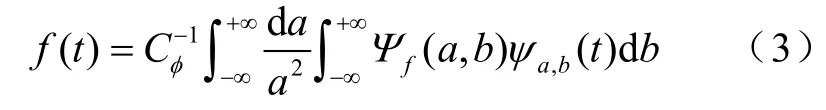
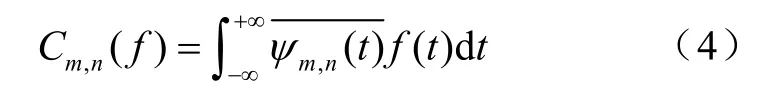
1986年，S.Mallat和Y.Meyer在多尺度逼近的基础上提出了多分辨分析（Multi-resolution Analysis，MAR）的概念[4]，多分辨分析只对低频部分进行进一步分解，而高频部分则不予考虑。Mallat在图像的分解与重构的塔式算法启发下，根据多分辨理论，提出了小波分解与重构的快速算法，称为Mallat算法[5]。

在Mallat算法中，小波分解通过一系列的滤波实现[6]，如图 2所示，图中方框中的滤波器用相应的系数来代替。信号s经过高通滤波器 h1，得到小波系数 c D1；经过低通滤波器 h0，得到尺度系数 c A1。由于经过滤波后的信号频带变窄，根据 Nyquist采样定律，只取一半采样点就可以表示原信号的所有信息，所以此时对 c D1和 c A1，分别进行二抽取，即将序列每隔一个去掉一个，使其长度减半。

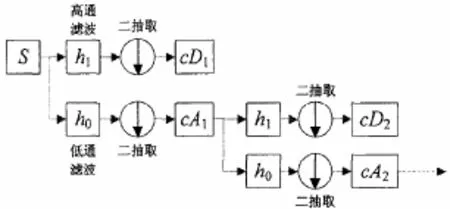
图2 多分辨率分解算法

设尺度函数为φ（t)，对应的小波函数为φ(t)，由多分辨分析可定义：

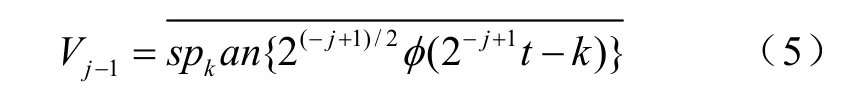
那么任意 f ( t)= Vj-1在 Vj-1空间的展开式为

将 f ( t)分解一次，即分别投影到 Vj、 Wj空间，则有分解公式

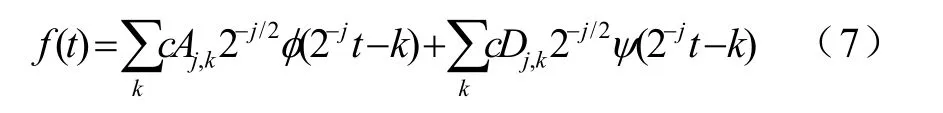
此时， c Aj,k和 c Dj,k为尺度j上的展开系数，且

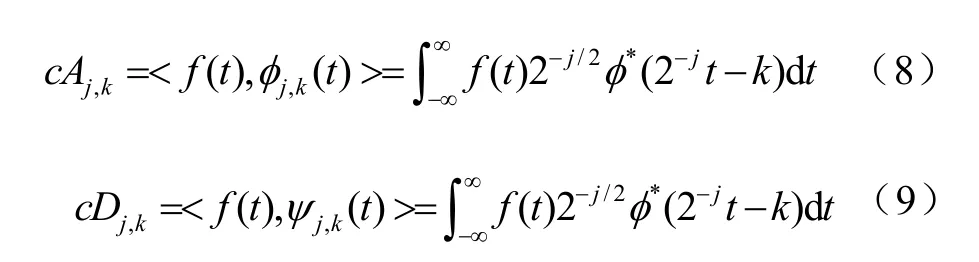
式中， c Aj,k为尺度系数， c Dj,k为小波系数。

经变换得

同理可得

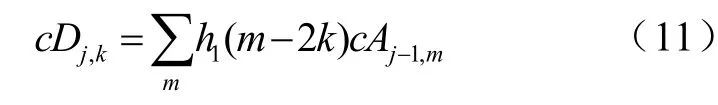
当待分析信号的采样频率满足 Nyquist 采样定理时，归一频率必须限制在-π～π之间，因此可分别用低通与高通滤波器 H0与H1将它分解成频带在0～π/2的低频部分和频带在π/2～π的高频部分，分别对应信号的主体和在0～π/2的高频部分，分别对应信号的主体和细节，如图3所示。

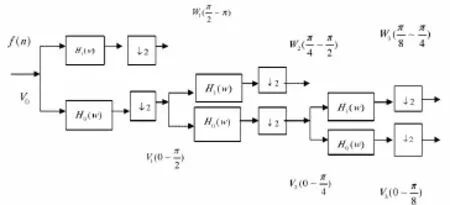
图3 频带的逐级剖分

用类似于信号分解的思路可以得到重构的过程，设 f ( t)∈ Vj-1，可以得到

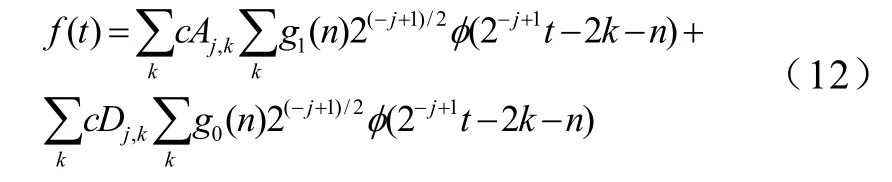
上式两边同时对 φj-1,m(t)进行内积，并且由于不同尺度上的尺度函数间具有正交性，得小波变换系数的重构公式

下图利用各个尺度的小波系数 c Dj和尺度系数cAj来重构原信号的过程。

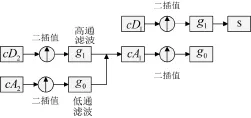
图4 多分辨率重构算法

从图中可以看到，对原信号的重构过程包含着“二插值”和滤波。二插值是二抽取的逆过程，也就是在序列的每两个相邻采样点之间填补一个0，使信号的长度加倍。滤波器系数使用的就是上面提到的 g1和 g0。第i级的小波系数 c A1，和尺度系数 c Aj，经过二次插值和滤波后，相加就得到了第 i + 1级的平滑逼近系数。如此递推，最后就可以根据 c D1和 c A1得到原信号了。

3 仿真算例

设电网的标准信号

可见信号中含有基波、3、5、7次谐波，其中基波频率为 50 Hz。现对信号进行采样，采样频率为5000Hz，在一个基波周期内的采样数据为100个点。现用FFT对信号进行频谱分析，原始信号如图5所示。

频谱图如图6所示。

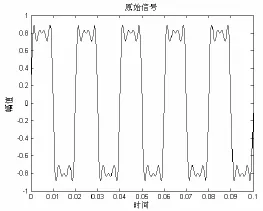
图5 原始仿真信号图

图6 FFT分析的信号功率频谱图

从图中看不出任何频域的性质，但从信号的功率频谱图中，可以明显地看出该信号是由频率为50Hz、150Hz、250Hz和350Hz的正弦信号组成的，也可以明显地看出信号的频率特性。Fourier变换将信号变换成纯频域中的信号。在频域中，傅里叶变换具有较好的局部化能力，但同时却不具有时间分辨的能力，对傅里叶谱中的某一频率，不知道这个频率是什么时候产生的[7-9]。

下面采用离散小波变换对信号模型进行仿真分析。因为信号中主要包含奇次谐波，尤其是3，5，7次谐波，在选择频带是不能太大，否则不能准确测量每次的谐波含量[10]。仿真信号的基频为 50Hz，每周期的采样点为100，采样频率为5000Hz，频带划分如表1所示。

表1 频带的划分

利用db8小波系对原始信号进行5层小波分解的结果，如图7所示。可以看出：原始信号中的不同频率的正弦信号分离开了。

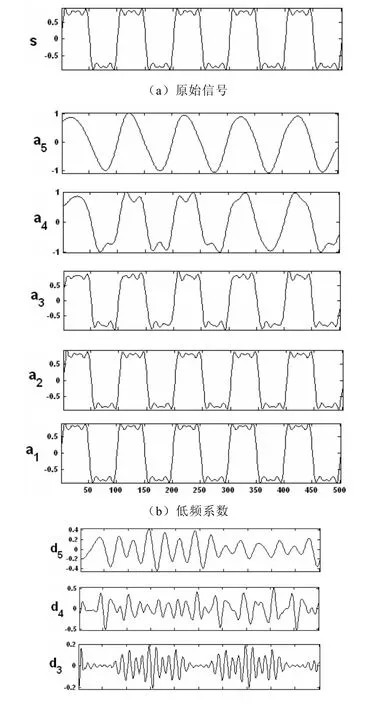
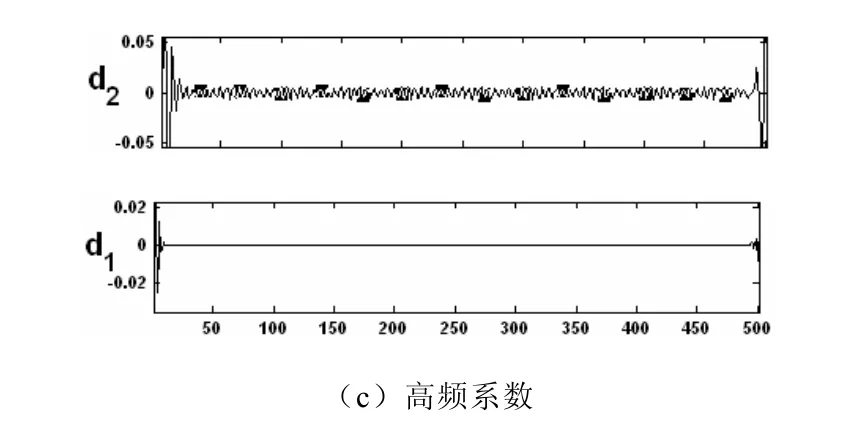
图7 不同频率分解图

低频系数A5其所在频带范围内仅有基波信号，所以A5重构得基波分量，高频系数D3～D5对应的频带范围仅含350Hz，250Hz，150Hz的信号，重构后得到3次，5次，7次谐波的波形，谐波分别如图8所示。从以上仿真结果可以看出，利用db8小波分解后各频带的信号被清晰得分解出来，时频特性也得到很好的体现。经过逆过程重构可以很好得到信号谐波，达到了检测谐波的目的。

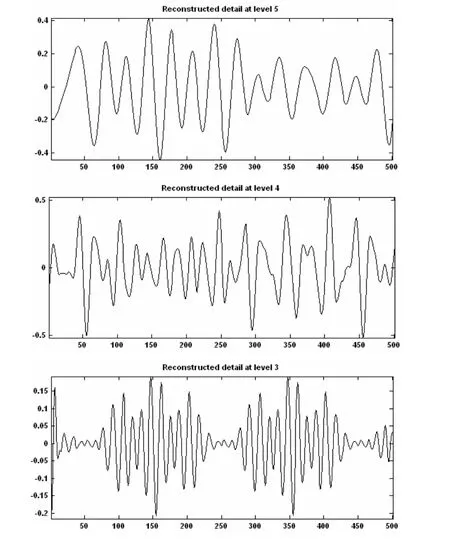
图8 谐波分量重构

4 谐波治理分析

根据以上分析实际谐波数据设置5次、7次、11次和13次等4组单调谐滤波器以滤除这几次超限严重的谐波电流[1]，再设置一组二阶高通滤波器滤除14次及以上次数的超限谐波电流。

单调谐波器是利用L、C谐振的原理构成的，电路原理如图9（a）所示，通常采用C、L、R串联排列。

图9 单调谐滤波器

n次单调谐滤波器在角频率 ωn=nω1时的阻抗为

式中， ω1= 2 π f1= 1 00π 为工频角频率， Rfn为n次谐波电阻， Zfn为n次谐波阻抗。根据式（15）画出滤波器阻抗随频率变化的关系曲线，如图9（b）所示。二阶减幅滤波器是最常用的高通滤波器，其电路结构和阻抗频率特性曲线不再详细叙述。据开始制定的方案和滤波器的原理，确定各滤波器参数如表2所示。

表2 各无源滤波器设计参数

用Matlab编写仿真程序进行数据仿真，滤波前后系统谐波电流幅值的簇状柱形图如图10所示，阻抗频率曲线如图11所示。

图10 滤波前后谐波电流幅值的柱形图

从图中可以看出5次、7次、11次、和13次以及高次谐波得到了明显地抑制，说明了谐波治理具有良好的效果。

5 结论

本文利用小波变换分析电网谐波的时频特性，通过仿真可以看出小波变换相对于傅里叶变换的优势，小波变换对信号分析的灵敏度高，且比较精确，并且逆过程重构可以很好得到信号谐波，它在电力系统谐波信号分析中具有很广的应用前景。最后通过设计无源滤波器对实际电网特定次超限谐波进行了治理，使谐波得到了改善。

[1]罗安.电网谐波治理和无功补偿技术及装备[M].中国电力出版社,2006:34-38.

[2]戴文,魏淑艳,曹明革.小波变换在谐波检测中的应用研究[J].电子测量技术,2011,34(7):37-39.

[3]薛蕙,罗红.小波变换与傅里叶变换相结合的暂态谐波分析方法[J].中国农业大学学报,2007,12(6):89-92.

[4]张斌，孙静.基于Mallat算法和快速傅里叶变换的电能质量分析方法[J].电网技术,2007,31(19): 35-39.

[5]刘俊,戴本祁,王之悦.基于小波和短时傅里叶变换的电网谐波分析[J].继电器,2007,35(23):55-59.

[6]黄文清，戴瑜兴，全慧敏.基于Daubechies小波的谐波分析算法[J].电工技术学报,2006,21(6):45-48.

[7]易立强，邝继顺.一种基于FFT的实时谐波分析算法[J].电力系统及其自动化学报,2007,19(2):98-101.

[8]胡海兵,祁才君,吕征宇.一种基于非同步采样的 FFT算法[J].中国电机工程学报,2004,24(12):13-17.

[9]刘鲭洁,陈桂明,刘晓方,占军.FFT和小波变换在信号降噪中的应用[J]. 数据采集与处理，2009，60(3):3-8.

[10]梁玉娟,李群湛,赵丽平.基于小波分析的电力系统谐波分析[J].电力系统及其自动化学报,2003,15(6):66-69.