星载单频GPS数据的电离层延迟改正方法分析

屈小川 李征航 龚晓颖

（武汉大学 测绘学院，武汉 430079）

星载单频GPS数据的电离层延迟改正方法分析

屈小川 李征航 龚晓颖

（武汉大学 测绘学院，武汉 430079）

利用C/A码单点定位对LEO（Low Earth Orbit）卫星上的电离层延迟改正方法——“电离层比例因子法”进行了分析研究.计算的CHAMP卫星的轨道结果表明:采用电子密度峰值高度（hmF2，F2 region maximum electron density height）平均值和瞬时值计算的电离层比例因子α变化范围分别为0.3～0.4和0.2～0.65之间，两者最大差异可达0.3，相比较而言，hmF2瞬时值的结果更加合理，并且相应的大地高H方向的系统偏差要降低0.05～0.3 m左右;与双频无电离层组合的普通单点定位结果相比表明该方法能较好地消除电离层一阶项所引入的H方向上的系统偏差;该方法适用的LEO卫星轨道高度范围大致在200～600km之间，当轨道高度超过700 km时，该方法并不适用.

单频GPS接收机;电离层比例因子法;单点定位;电子密度峰值高度

通常情况下，在LEO（Low Earth Orbit）卫星运动学法定轨中，利用所搭载的GPS接收机的双频观测数据，可以很好地消除电离层延迟的一阶项的影响，联合其他相关精密产品，从而可以精确地确定LEO轨道，但是出于国防安全、价格等方面的考虑，我国发射的科学实验卫星所搭载的GPS接收机一般都是自主研发的单频接收机，并采用C/A码单点定位的方法进行实时定轨，这也就无可避免地存在观测数据精度低和电离层延迟无法自主校正等问题，其中电离层延迟如何改正是提高C/A码单点定位精度的关键.2002年，文献［1］给出了一种“电离层比例因子法”的方法的思想，但并未对电子密度峰值高度hmF2的确定原则作说明，也未对该方法的通用性作进一步分析.郑磊等人利用IRI2007确定的hmF2平均值来验证该方法在不同太阳活动情况下的通用性［2］，但由于hmF2的时空变化特性，用平均值代替会造成电离层延迟改正不完全，且也未对不同轨道高度的LEO卫星分析该方法的适用性.针对上述问题，本文利用CA码单点定位的方法对“电离层比例因子法”的改正效果和适用性进行分析研究.

1 电离层比例因子法

LEO卫星的轨道高度一般在200～1 000 km之间，其只受轨道以上部分电离层延迟的影响，因此LEO卫星进行C/A码单点定位的电离层延迟改正方法略微不同于地面站.2002年，文献［1］给出了一种“电离层比例因子法”，其基本思想是:利用Chapman电子密度剖面函数［3］，计算LEO卫星轨道高度以上的电子含量占总电子含量的比例因子α，若能获得总电子含量TEC，再乘以比例因子α即可获得LEO轨道高度以上的电子含量，从而求得LEO卫星所受到的电离层延迟值.

首先，利用Chapman电子密度函数计算电离层比例因子α:

式中，z=（h－h0）/H;h0为电子密度峰值高度hmF2;H为电子密度高度变化率，一般取值100 km;Ne0为电子密度峰值.

与地面站建立的电离层单层模型类似，也假设LEO卫星所受到的电离层延迟集中于某一个单层高度hIP（hs＜hIP，见图1），为确定单层高度hIP，需设定一个比例系数m，即

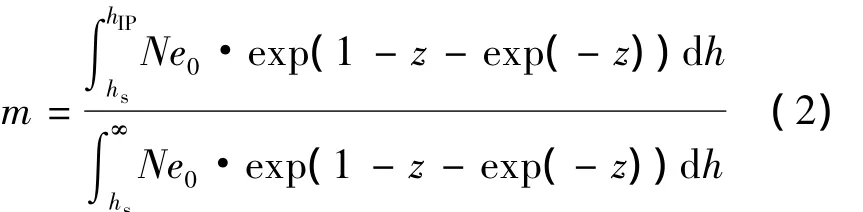
在文献［1］中取m为0.5，即取占LEO轨道高度以上的电子含量50%的位置处为单层高度.若能获得穿刺点处的hIP值，并根据式（3）即可求得相应观测方向上的电离层延迟改正值.

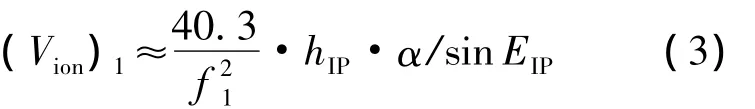
式中EIP为穿刺点处的高度角.

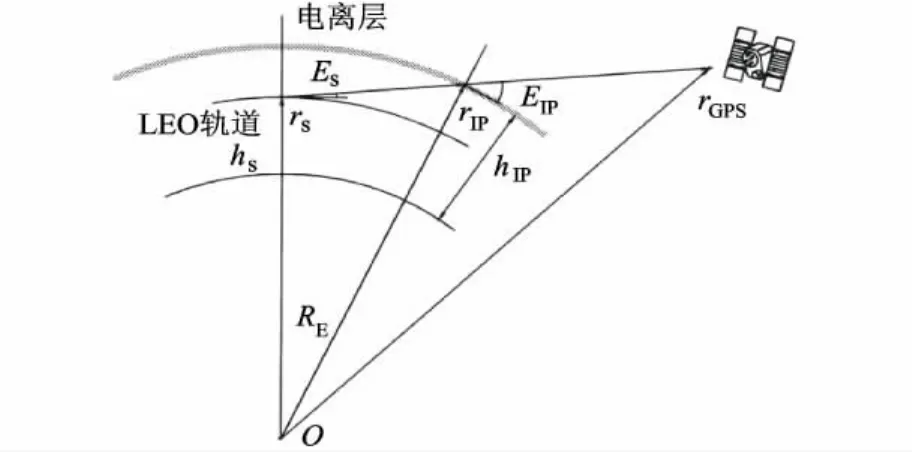
图1 电离层比例因子法的几何示意图

文献［1］在计算比例因子α时的起始积分高度为hIP，郑磊等人认为积分高度取hs更为合理，笔者认为当积分高度为hs时，理论上更为严谨，因此在下列计算中积分高度均取hs，不过郑磊等人在积分的过程中取电子密度峰值高度hmF2为某一天或一年的算术平均值，笔者认为并不合理，因为峰值高度变化比较复杂，不仅随经纬度变化，还随时间变化.本文利用IRI 2007模型计算得到2008-01-01T4∶00 ∶00（UTC）时的峰值高度 hmF2全球变化图（见图2），图2中可以看出不同地区的峰值高度hmF2差值最高可达200 km，尤其是赤道地区一天中的峰值高度变化可达150 km，而且还存在季节性变化，因此若峰值高度hmF2取某一平均值很大程度上会影响LEO卫星电离层延迟的改正效果，从而影响定轨结果，这点后面将要讨论分析.

图2 电子密度峰值高度hmF2变化图

2 数据处理策略

由于LEO卫星的轨道高度位于200 km以上，基本不受对流层延迟等误差的影响，当高度角大于10°时，多路径效应也可以忽略不计，而受到电离层延迟误差、卫星星历误差及钟差等误差的影响，因此利用C/A码单点定位的观测方程为

3 数据处理及分析

2000年，GFZ发射了 CHAMP卫星，为地磁场、重力，以及大气等方面的分析研究提供了大量的数据资料，其轨道参数见表1.为便于分析比较，本文按下列3种单点定位方式处理了CHAMP卫星的GPS数据:①未进行电离层延迟改正的C/A码单点定位;②利用“电离层比例因子法”进行电离层延迟改正的C/A码单点定位;③伪距无电离层组合P3单点定位;并把3种定轨结果分别与JPL提供的CHAMP科学轨道产品进行比较.

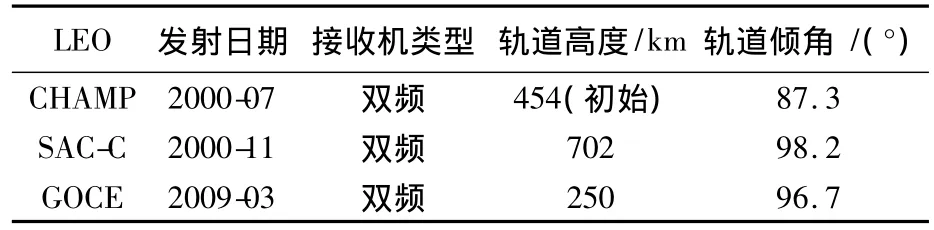
表1LEO卫星

3.1 hmF2 的影响

从公式（1）可以看出，电离层比例因子α的取值不仅与轨道高度hs相关，而且还与峰值高度hmF2相关，由于LEO卫星的运行周期较短，如CHAMP卫星一天可以绕地球飞行15圈左右，并且随着地球的自转，LEO卫星位置处的峰值高度hmF2的变化幅度较大，因此取某一平均值的做法会影响到比例因子α的大小，影响电离层延迟的改正效果，并进一步影响到定轨精度.本文利用2005-01-03的CHAMP卫星的GPS观测数据计算分析采用2种峰值高度情况下的定轨精度.在数据处理过程中剔除了GDOP大于10，单位权中误差大于2.5的平差值，并把定轨结果分别与JPL轨道产品在BLH 3个方向较差，并求出相应的平均值和均方差（RMS，Root Mean Square）.根据IRI 2007模型计算得到了当天的峰值高度的平均值为291.114 km.

表2给出了当峰值高度分别取平均值和瞬时值时的定轨精度.从表2中可以看出B，L方向上的定轨精度变化并不大，这是由于电离层延迟主要反映在大地高H方向上，而B，L方向的定轨精度对其并不敏感.虽然H方向上的RMS值相差不大，约为0.04 m，但是由于采用hmF2平均值计算的电离层比例因子α不准确，使得电离层延迟改正不完全，从而导致H方向上引入了约0.23 m左右的系统偏差，本文认为这是合理的，因为LEO卫星在绕地球运行过程中的覆盖范围很大，且不同时间、不同地区的峰值高度是不同的，最大差值可达200 km，因此峰值高度取平均值这一做法会影响到电离层比例因子α的取值，造成在某一位置的α过大，或某一位置的α过小，进而造成电离层延迟改正值偏大或偏小，与瞬时值的定轨精度相比，会在H方向上引入一个系统偏差.

表2 峰值高度hmF2对定轨精度的影响

图3给出了当峰值高度hmF2分别取平均值和瞬时值时计算得到的电离层比例因子α，从图3中可以看出α的波动范围分别在0.3～0.4和0.2 ～0.65 之间，两者最大差值可达 0.3.根据式（1）知道，当峰值高度hmF2与LEO卫星的轨道高度非常接近时，这时候α的大小是有可能超过0.5的，即LEO卫星受到的电离层延迟值有可能超过总延迟值的一半，这也与实际情况相符，由于受到大气阻力以及太阳活动不同程度的影响，CHAMP卫星的轨道高度不断降低，2005年其最低轨道高度已经接近365.00km，而从图2可以看出某些位置的峰值高度已经超过了365.00km，并且有些LEO卫星的轨道高度较低，如GOCE卫星，如果仍然使用峰值高度的平均值来计算α，使得电离层延迟改正并不完全，从而会在H方向上引入系统偏差.

图3 两种峰值高度情况下的电离层比例因子α

为进一步验证峰值高度对定轨精度的影响，根据两种峰值高度确定方法，本文计算了2007年CHAMP卫星的GPS观测数据，并与JPL的科学轨道产品比较.限于篇幅，仅给出H方向上的平均值，由于某些天缺乏JPL轨道数据，以及GPS数据质量问题，总共有360 d参与比较（图4）.

图4 2007年H方向上定轨偏差平均值

图4中可以看出，除个别天数外，利用峰值高度瞬时值计算的CHAMP轨道的H方向上平均值比峰值高度平均值计算得到的H方向平均值普遍较小，两者差值基本在0.05～0.3 m范围内波动，本文认为这是由于利用峰值高度平均值计算电离层比例因子是不准确的，使得电离层延迟改正不准确，从而在H方向上引入了系统偏差.

3.2 与P3单点定位结果比较

对CHAMP卫星的2008-01-10的GPS数据进行处理，处理原则同上一节，并把3种定轨结果分别与JPL的科学轨道产品进行比较，求出BLH方向上的平均值和RMS（见表3）.从表3中可以看出3种定轨方法在B，L方向上RMS差别不大，精度几乎相当，原因同上一节，此处不再赘述.同时从表3中看出，与另外两种定轨方法相比，未进行电离层延迟改正的C/A码单点定轨在H方向上存在2.8018 m的系统偏差，这主要是由电离层延迟误差引起的，经过电离层延迟改正后的C/A码单点定位在H方向上的系统偏差仅为0.3849 m，且定轨精度由4.298 0 m提高到3.6958 m，而P3普通单点定位的H方向平均值为0.2114 m，RMS值为3.575 2 m，两者基本相当，这表明该方法能较好地消除由电离层延迟一阶项所引起的H方向上的系统偏差.

为便于分析比较，本文计算了2005年3月份共31d的CHAMP卫星的GPS数据，限于篇幅，本文仅给出H方向上的平均值和RMS（见图5）.从图5可以看出，经过“电离层比例因子法”改正后，C/A码与P3的H方向上的平均值基本都在零均值附近波动，而两者的RMS值的图形几乎一致，这表明当LEO卫星利用C/A码观测值进行定轨时，“电离层比例因子法”能很好地消除电离层延迟一阶项所引入的H方向上的系统偏差.

表3 3种定轨结果与JPL轨道产品比较

图5 3种方法在H方向上的定轨精度

3.3 轨道高度的影响

为验证“电离层比例因子法”在不同LEO卫星轨道高度情况下的适用性，本文计算了3种不同轨道高度的LEO卫星的C/A码单点定位结果:SAC-C，CHAMP和GOCE，相应的卫星参数见表1.考虑到电离层延迟对B，L方向上的定轨精度影响很小，图6仅给出了 SAC-C、CHAMP和GOCE的定轨结果与科学轨道产品在H方向上的偏差值.由于SAC-C和CHAMP卫星的科学轨道产品是由JPL提供，而GOCE卫星的科学轨道产品是由ESA提供，故它们的时间间隔不同.

从图6a中可以看出由于SAC-C卫星的轨道高度在700 km以上，所受电离层延迟已经很小，因此是否进行电离层延迟改正，这对C/A码单点定位精度的提高几乎无影响，因此图6a中给出的电离层延迟改正前后定轨偏差图几乎完全相互覆盖，这与实际情况非常符合，当LEO卫星轨道高度超过700 km时，可不进行电离层延迟改正而直接利用C/A码观测值进行单点定位来解算获取相应的轨道参数.图6b和图6c中给出CHAMP和GOCE卫星的定轨偏差图类似，“电离层比例因子法”能很好地改正CHAMP和GOCE卫星受到的电离层延迟误差，从而提高相应的定轨精度，不过也可以看到当LEO卫星轨道高度较低时，所受到的电离层延迟较大，而“电离层比例因子法”改正的幅度相对来说也较大，即GOCE卫星的改正幅度较CHAMP卫星要大.

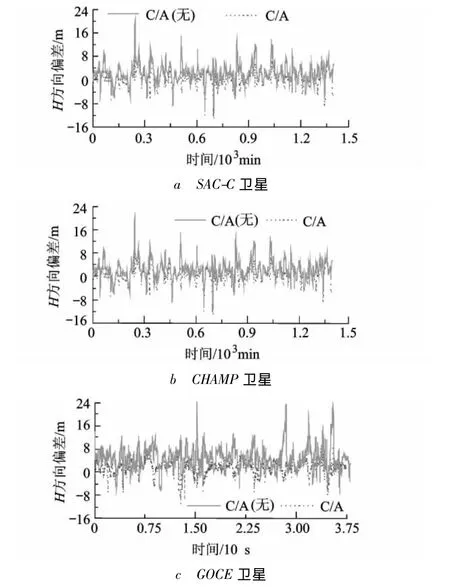
图6 电离层延迟改正前后H方向的定轨偏差

4 结论

对LEO卫星上的电离层延迟改正方法——“电离层比例因子法”进行了分析研究，得出以下结论:①当LEO卫星利用C/A码单点定位的方法获取粗略的卫星轨道值时，“电离层比例因子法”能很好的消除由于电离层延迟一阶项所引起的大地高H方向上的系统偏差.②与峰值高度hmF2平均值相比，采用瞬时值计算得到的电离层比例因子α更加准确，更加合理，从而降低由于采用不准确的峰值高度hmF2而在大地高H方向引入的系统差，量级在0.05～0.3 m 之间.③当LEO卫星轨道高度超过700 km时，由于所受的电离层延迟值较小，“电离层比例因子法”并不适用，而能够适用于轨道高度在200～600 km左右的LEO卫星.

本文在分析“电离层比例因子法”时，未顾及定轨的实时性，而采用了CODE提供的球谐函数系数产品CODE＊＊＊＊＊.ION，且为便于比较，本文采用的是双频接收机获得的单频数据，而实际的单频接收机可能因数据质量较差使得定轨精度要低于上述情况.

致谢 感谢CODE提供的相关电离层产品，JPL提供的SAC-C和CHAMP卫星的GPS数据和轨道产品，以及ESA提供的GOCE卫星的相关数据和产品.

（References）

［1］Montenbruck O，Gill E.Ionospheric correction for GPS tracking of LEO satellites［J］.The Journal of Navigation，2002，55（2）:293－304

［2］郑磊，李征航，刘万科.用星载单频GPS数据实时定轨的电离层延迟改正［J］.大地测量学与地球动力学，2010，30（3）:118－121

Zheng Lei，Li Zhenghang，Liu Wanke.Correction of ionospheric delay for real-time orbit determination by using on-board singlefrequency GPS data［J］.Journal of Geodesy and Geomatics，2010，30（3）:118－121（in Chinese）

［3］Chapman S.The absorption and dissociative or ionizing effect of monochromatic radiation in an atmosphere on a rotating earth［J］.Proc Phys Soc，1931，43（1）:483－501

［4］Bilitza D，Reinisch B W.International reference ionosphere 2007:improvements and new parameters［J］.J Adv Space Res，2008，42（4）:599－609

［5］李征航，丁文武，李昭.GPS广播星历的轨道误差分析［J］.大地测量与地球动力学，2008，28（2）:50－54

Li Zhenghang，Ding Wenwu，Li Zhao.Error analysis of orbit determinated by GPS broadcast ephemeris［J］.Journal of Geodesy and Geomatcis，2008，28（2）:50－54（in Chinese）

［6］Schaer S.Mapping and predicting the earth's ionosphere using the global positioning system［D］.Bern:Astronomical Institute，University of Bern，1999

［7］Montenbruck O.Kinematic GPS positioning of LEO satellites using ionospheric-free single frequency measurements［J］.Aerospace Science and Technology，2003，7（5）:396－405

［8］Kuang D，Bar-Sever Y，Bertiger W，et al.Precise orbit determination for CHAMP using GPS data from BlackJack receiver［C］//Proceedings of the 2001 ION National Technical Meeting.Long Beach，CA，USA:［s.n.］，2001:762－770

［9］李征航，黄劲松.GPS测量与数据处理［M］.武汉:武汉大学出版社，2005

LiZhenghang，Huang Jinsong.GPS surveying and data processing［M］.Wuhan:Wuhan University Press，2005（in Chinese）

［10］王甫红，刘基余.星载GPS伪距测量数据质量分析［J］.测绘科学技术学报，2007，24（2）:97－99

Wang Fuhong，Liu Jiyu.Data quality analysis of space-borne GPS code measurements［J］.Journal of Zhengzhou Institute of Surveying and Mapping，2007，24（2）:97－99（in Chinese）

Analysis on ionospheric delay correction method of space-borne single-frequency GPS data

Qu Xiaochuan Li Zhenghang Gong Xiaoying
（School of Geodesy and Geomatics，Wuhan University，Wuhan 430079，China）

With the technology of standard point positioning based on C/A code

by low earth orbit（LEO），one of the ionospheric delay correction method，the method of ionospheric scale factor，was discussed.The computed ionospheric scale factor α using the mean and instantaneous value of F2 region maximum electron density height is 0.3 ～0.4 and 0.2 ～0.65 respectively，and the maximum difference between them reaches to 0.3.Comparatively，the latter coincides with the reality better，and it reduces the systematic error in the geodetic height direction by 0.05 ～0.3 m.With the comparison to the standard point positioning based on ionosphere free combination of the dual-frequency code measurements，the method could eliminate the systematic error in geodetic height induced by the first order of ionospheric delay.And the method could adapt to the LEO altitudes of about 200～ 600 km，but it’s useless at the altitudes more than 700 km.

single-frequency GPS receiver;the method of ionospheric scale factor;standard point positioning;F2 region maximum electron density height

P 228

A

1001-5965（2012）02-0252-05

2010-10-11;< class="emphasis_bold">网络出版时间:

时间:2012-02-21 11:46;

CNKI:11-2625/V.20120221.1146.008

www.cnki.net/kcms/detail/11.2625.V.20120221.1146.008.html

国家863计划项目资助项目（2009AA12Z301）

屈小川（1984－），男，安徽阜阳人，博士生，qqxxcc@hotmail.com.

（编 辑:张 嵘）