高超声速尖锥边界层转捩数值模拟
宋 博 李椿萱
(北京航空航天大学 航空科学与工程学院,北京100191)
边界层转捩对高超声速飞行器的气动力、热产生重要的影响,因此转捩的精确预估对飞行器气动和热防护系统的设计极为重要[1-2].然而,边界层的转捩受当地Mach数、单位Reynolds数、壁面冷却效应、头部钝度 (包括entropy swallowing效应)、横流或三维流动效应、壁面粗糙度、吹吸等流动和几何参数的影响[3-4],且这些因素相互干扰、耦合,难以精确模拟,以致迄今仍未能建立起完整的转捩理论,特别是高超声速边界层转捩的预测仍是尚未解决的流体力学难题.
基于层流脉动能 (laminar kinetic energy)的转捩位置判断方法在近年来受到了较多的关注.该方法的基本思想是转捩的发生是由层流中存在的不稳定波动引起的,从而通过模拟层流区域的脉动能发展过程来构造转捩的预测模型.这种基于不同物理机理引发的转捩模拟模式是对以往强烈依赖于经验的模式的一个重大改进.文献[5-7]最先应用稳定性理论导出了不同扰动模态的涡粘性.文献[8-10]通过一系列数值实验验证了高超声速条件下该模式是相当有效的.
然而,文献[8-10]的所有算例均假设转捩过程为自然转捩,但所参考的实验结果均出自常规风洞,其壁面湍流边界层所产生的噪声要比飞行实验中观测到的高出一个量级,造成小扰动诱发自然转捩的实验呈现出逾越型 (bypass)转捩机制,导致转捩位置较飞行实验的结果大大提前,同时机制的不同可令转捩参数的影响趋势随之改变[11].静风洞的实验段近壁流动为层流,其环境噪声接近于高空的真实情况.本文作者曾在Favré(密度加权)平均的框架下推导了可压缩流动的层流脉动能输运方程,在一定的假设下结合尺度分析针对方程中出现的显式可压缩项进行了封闭,并采用静风洞转捩实验的数据对所建立模型的模型系数进行了标定[12-13].本文将采用上述已标定系数的模型开展高超声速尖锥边界层转捩位置的数值预测研究.
1 基于Favré平均的层流脉动能方程
Favré平均N-S方程的具体形式参见文献[4].通过推导Favré平均可压缩Reynolds应力方程,再对方程中的Reynolds应力张量进行收缩可导出笛卡儿坐标系下基于Favré平均的层流脉动能输运方程:
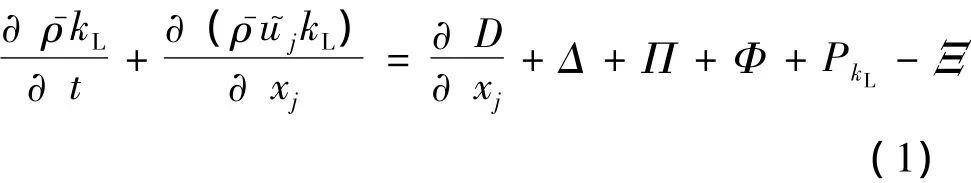
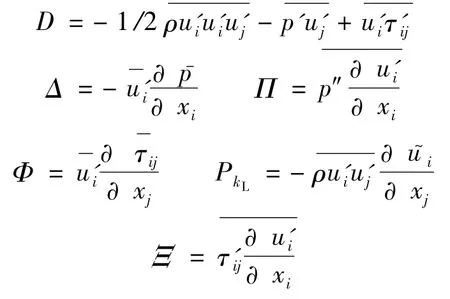
其中,上标“~”与“'”分别代表流场变量的Favré平均量及其脉动;上标“-”与“″”分别代表流场变量的时间平均量及其脉动.
方程 (1)右端项的简化和封闭可参阅文献[12],在此仅给出其最终形式:
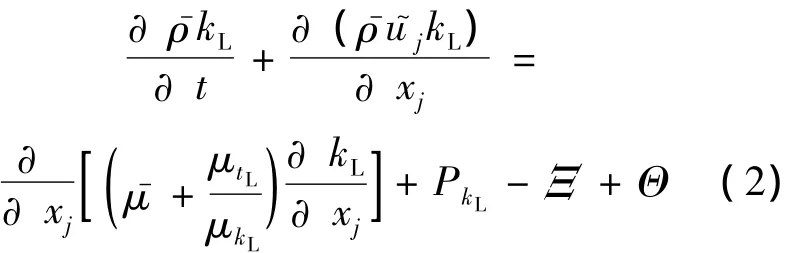
其中

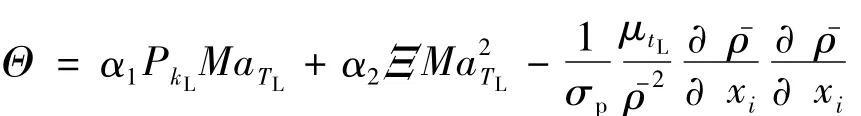
其中MaTL为脉动马赫数,定义为
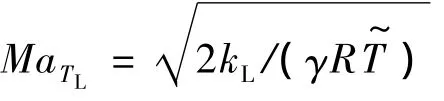
μtL为层流脉动的涡粘性,与诱导转捩发生的不稳定波动的特性有关,可写成[7]

Cμ为常数,取值0.09;τtL为层流脉动的时间尺度,可表达为
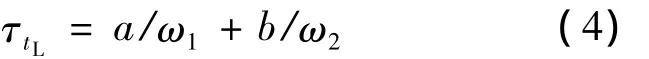
ω1和ω2分别表示最不稳定的第一、第二模态波动的频率,可表示为
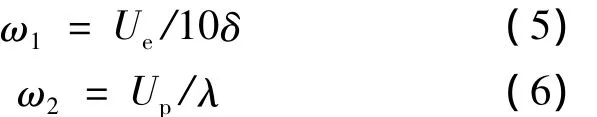
δ为速度边界层厚度;Ue和Up分别为边界层的边缘速度和相速度,有Up≈0.94Ue;λ为流场的特征长度,取λ≈2δ.
在上述模型中,模型系数的取值为[12]
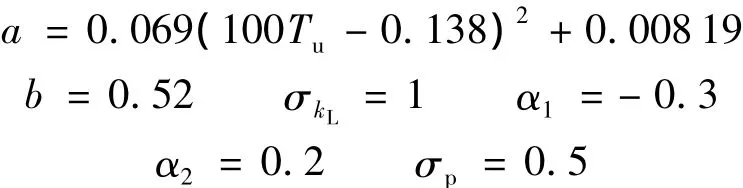
其中Tu表示来流脉动强度,定义为
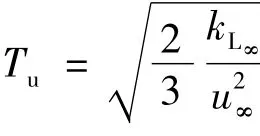
转捩的预测可通过对式 (2)与Favré平均Navier-Stokes方程组的联立求解给出.其转捩准则设定为:流场中满足
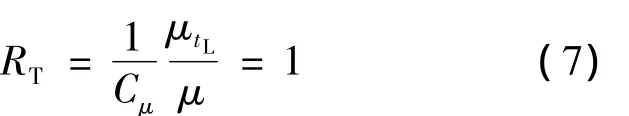
的第1个点对应的流向坐标xt即被认为是转捩的起始位置.
上述基于层流脉动能输运的边界层转捩预测模型包含了一定的物理机理.可以看到,式(2)右端各项均依赖于层流脉动涡粘性系数μtL.其计算式 (3)中显含了流场的特征时间尺度,该时间尺度是流场中最不稳定波动的频率的函数,而最不稳定波的频率与引发转捩的物理机制密切相关.更多关于不稳定波动频率的讨论可参阅文献 [14].
2 数值模拟参数研究
本文采用隐式方法计算定常层流流动,采用显式方法进行转捩位置预测计算.对控制方程中无粘和粘性通量项的差分离散分别采用了Harten-Yee TVD格式和二阶中心格式.在获取层流平均流场后,即可将Favré平均层流脉动能方程与N-S方程组进行联立求解以给出转捩的位置.
2.1 单位Reynolds数效应
2.1.1 算例说明
文献 [15]进行了半角为5°尖锥的高超声速边界层转捩实验研究.实验模型的头部半径为2.54×10-6m,来流 Mach数为6.0,攻角为0°,总压为3.34×105Pa.8组实验 (H1~H8)的来流单位长度Reynolds数Re∞的变化范围为3.6×106m-1~25.6×106m-1.实验分别对绝热 (Tw/T0∞=0.86)和等温 (Tw/T0∞=0.59)壁面条件下的流场进行了测量.
为考察文献 [12]所建立的高超声速可压缩转捩预测模型对Reynolds数效应的捕捉效果,本节将以与上述转捩流动实验相同条件的尖锥绕流为算例开展数值模拟参数研究.算例采用等温壁条件.所采用的流向、法向和周向网格点数分别为201,101和37.流向网格采用均匀分布,法向网格在壁面附近进行了加密.
2.1.2 边界层转捩位置预测结果
在转捩预测计算中,对边界层厚度的估算在此提出采用基于当地总焓峰值的准则.数值实验表明,采用该准则可给出更为准确的边界层厚度.在此,仅以算例H1为例,图1给出了模型子午面上 x=0.1,0.3,0.5和0.8 m处的无量纲切向速度和以来流总焓无量纲化的无量纲总焓剖面.可以看到,在速度边界层外缘附近,总焓峰值位置接近速度边界层外缘,并在流动下游具有更好的吻合度,从而证实了基于总焓峰值的边界层厚度判断准则亦适用于等温壁面条件的流动.
考虑到本算例所引的实验是在生产型常规风洞中进行的,模型参数b的取值在此沿用文献[8-10]在数值模拟高噪声环境下转捩实验的做法,即令b=a.然而文献 [8-10]在其工作中假设了第二模态与横流模态的影响可合并表达为ω2=Up/λ',其中 λ'≈3.5δ.在上述假设下,文献 [9]数值模拟了Horvath实验,并标定了实验所用NASA LaRC 20”Mach 6风洞的湍流度Tu为0.67%.然而,采用该Tu值在本文的转捩预测模型框架下进行的数值计算发现,转捩位置与实验结果相比大大提前.作者认为,这缘于Papp转捩预测模型[8-10]中 ω2的表示形式并不适用于本节所研究的轴对称尖锥流动,因为在零攻角状态下横流模态并不起作用;而考虑横流模态后令λ'≈3.5δ的处理方式相当于减小了第二模态的频率,即增大了其特征时间尺度.由式(3)可知该时间尺度的增大将加速层流脉动涡粘性的增长,从而导致转捩过早发生.
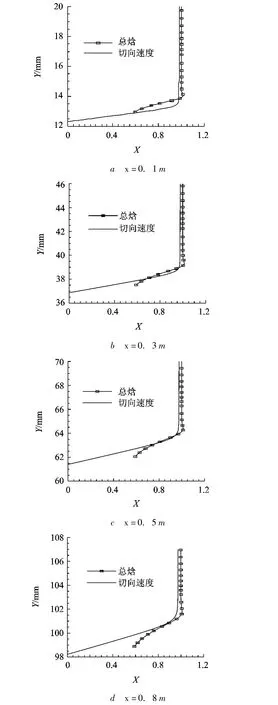
图1 尖锥子午面上无量纲切向速度和无量纲总焓剖面
基于上述讨论,在此采用本文建立的可压缩转捩预测模型对算例H4进行了一系列不同来流湍流度下的数值模拟实验,并由此将来流湍流度重新标定为0.435%.应用该标定值进行数值模拟所得的算例H1~H8的转捩起始位置见表1所列.

表1 Reynolds数效应算例转捩起始位置计算结果 m
可以看到,计算结果与实验值吻合较好,特别是算例H2~H4,二者的误差小于2%.随着来流单位Reynolds数的增大,转捩位置逐渐向头部靠近.然而当来流单位Reynolds数较大时(算例H5~H8),计算转捩位置与实验结果相比存在一定的滞后.一个可能的原因是此时层流脉动能在模型头部下游快速增长,而数值计算采用的网格在头部附近较稀,其流向分辩率不足,从而令脉动能的耗散过大,造成了转捩的延迟.
2.2 攻角效应
三维效应对高超声速飞行器边界层内不稳定波动的发展规律和转捩位置的影响一直是研究的重点.在高超声速条件下,三维边界层转捩的主导模态是横流模态.有攻角圆锥边界层是典型的三维边界层.考察高超声速尖锥 (半锥角小于10°)攻角对边界层转捩影响的风洞实验可以得到较为一致的结论:小攻角 (小于5°)条件下,与零攻角时相比,背风子午线上的转捩位置前移,迎风子午线上的转捩位置后移,且该趋势随攻角的增大而增大.然而,由于三维高超声速边界层转捩过程受实验环境噪声、来流Reynolds数、Mach数、攻角以及锥角等多重因素的影响,实验数据存在相当大的离散度.静风洞的环境噪声水平接近于真实飞行环境的噪声,其实验数据应具有更高的参考价值,但作者未搜集到研究高超声速尖锥攻角效应的静风洞实验的相关文献.
2.2.1 算例说明
本节将选用5°半角的尖锥模型,对其在攻角 α =0°,0.5°,1°,2°下的绕流流场进行数值模拟参数研究,分析小攻角状态下的流场特征并采用本文所建立的可压缩转捩预测模型预估不同攻角下的转捩位置.鉴于实施相关实验的常规风洞的噪声水平可对边界层转捩位置造成显著影响,而目前对其尚无准确可信的标定值,且为便于对比分析攻角对转捩位置的影响,在此计算的来流条件采用与静风洞尖裙锥绕流实验相同的条件[12];转捩预测计算时来流湍流度取值为Tu=0.1%,参数b取值0.54;壁面采用绝热壁边界条件.
2.2.2 边界层横流转捩预测的数值模拟结果
应该指出,为了显式表征高超声速三维边界层转捩的横流模态,在三维边界层转捩预测计算时,层流脉动的特征时间尺度应修正为
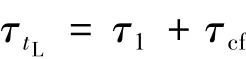
其中τcf表示横流模态的特征时间尺度,以特征频率表达有
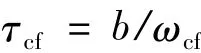
其横流模态的特征频率ωcf=Up/3.5δ.
采用本文作者所提出的可压缩转捩预测模型[12]计算得到的迎风子午面和背风子午面上的转捩起始位置见表2.可以发现,随着攻角的增大,其迎风子午面上计算所得到的转捩起始位置相比于零攻角呈单调增大,相当于迎风面上转捩延迟发生;在背风子午面上,转捩起始位置则单调减小,相当于背风面上转捩提前发生.但转捩延迟和提前的程度并不大,主要是由于计算所采用的网格在展向的细密度不足所致.即使如此,本项小攻角范围的参数研究所显示的攻角对转捩位置的影响趋势与高超声速边界层转捩风洞实验的结论是一致的.
此外,与零攻角尖裙锥绝热壁条件下的绕流计算结果[12]相对比可以发现,零攻角尖锥上的转捩位置存在显著延迟.该结果再次证实了文献[12]所得出的结论:逆压梯度可增强流动不稳定性,使转捩提前发生.
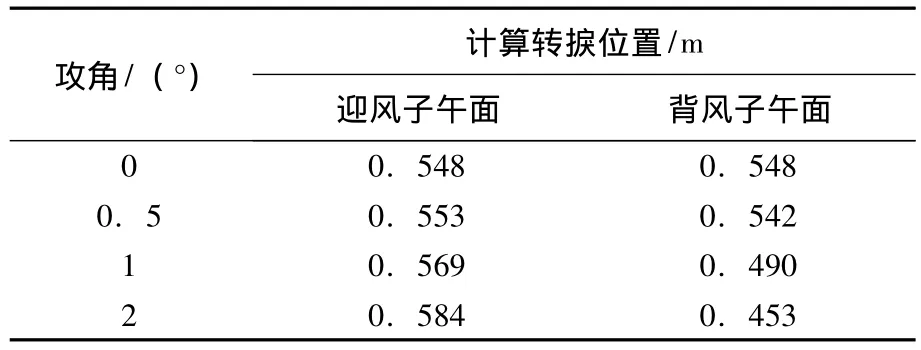
表2 攻角效应算例转捩起始位置计算结果
3 结论
本文通过对不同Reynolds数下绕尖锥的高超声速流动的系列数值实验研究了单位Reynolds数对轴对称边界层转捩位置的影响,结果表明增大单位Reynolds数可使转捩提前发生.随后对攻角为0.5°,1°和2°的三维尖锥边界层展开了数值模拟研究,计算并分析了转捩位置在圆锥迎、背风面的不同变化趋势,得到了与实验相一致的结论:迎风面上转捩延迟,背风面上则提前.
References)
[1]Lau K Y.Hypersonic boundary layer transition-application to high speed vehicle design[R].AIAA-2007-310,2007
[2]Papp J L,Dash S M.Hypersonic transitional modeling for scramjet and missile applications[R].AIAA-2002-0155,2002
[3]Morkovin M V.Transition at hypersonic speeds[R].NASACR-178315,1987
[4]Wilcox D C.Turbulence modeling for CFD [M].2nd ed.California:DCW Inc,2000:174-179
[5]Warren E S,Hassan H A.Transition closure model for predicting transition onset[J].Journal of Aircraft,1998,35(5):769-775
[6]Xiao X,Edwards J R,Hassan H A.Transitional flow over an elliptic cone at Mach 8[R].AIAA-2001-0276,2001
[7]McDaniel R D,Nance R P,Hassan H A.Transition onset prediction for high speed flow[R].AIAA-99-3792,1999
[8]Papp J L,Dash S M.Rapid engineering approach to modeling hypersonic laminar to turbulent transitional flows[J].Journal of Spacecraft and Rockets,2005,42(3):467-475
[9]Papp J L,Kenzakowski D C,Dash S M.Extensions of a rapid engineering approach to modeling hypersonic laminar to turbulent transitional flows[R].AIAA-2005-0892,2005
[10]Papp J L,Dash S M.A rapid engineering approach to modeling hypersonic laminar to turbulent transitional flows for 2D and 3D geometries[R].AIAA-2008-2600,2008
[11]Schneider S P.Effects of high-speed tunnel noise on laminarturbulent transition [J].Journal of Spacecraft and Rockets,2001,38:323-333
[12]Song B,Lee C H.A favré averaged transition prediction model for hypersonic flows[J].Science China,Technological Sciences,2010,53(8):2049-2056
[13]宋博,李椿萱.其于Favré平均的高超声速可压缩转捩预测模型[J].中国科学:技术科学,2010,40(8):879-885
Song B,Lee C H.A Favré averaged transition prediction model for hypersonic flows[J].Science China:Technological Sciences,2010,40(8):879-885(in Chinese)
[14]宋博,李椿萱.基于非湍流脉动动能方程的高超声速转捩预测[J].北京航空航天大学学报,2010,33(10):1162-1165
Song Bo,Lee Chunhian.A transition prediction model for hypersonic flows based on laminar fluctuation energy transport equation [J].Journal of Beijing University of Aeronautics and Astronautics,2010,33(10):1162 -1165(in Chinese)
[15]Horvath T J,Berry S A,Hollis B R,et al.Boundary layer transition on slender cones in conventional and low disturbance Mach 6 wind tunnels[R].AIAA-2002-2743,2002

