“数字信号处理”课程中线性相位的探讨

童晓兵，徐以涛，蔡跃明

(解放军理工大学通信工程学院，江苏 南京 210007)

线性相位是有限脉冲响应(FIR)数字滤波器的一个突出优点。在数据通信和图像处理等应用领域，往往要求信号在传输和处理过程中不能有明显的相位失真，因此具有线性相位的FIR滤波器在工程实践上得到了广泛的应用[1]。然而，在“数字信号处理”课程中线性相位的教学存在两个问题。一是学生很难理解相位的线性与非线性对信号的特性究竟会造成什么样的影响。二是线性相位FIR滤波器的推导过程比较繁琐复杂，学生的理解不够深刻[2]。本文重点针对这两个问题，结合笔者的教学经验提出一种新的教学方法，从另外一个途径加深学生对线性相位的理解。教学实践证明，这种方法具有良好的教学效果。

1 非线性相位对信号特性的影响

在线性相位的教学过程中发现，学生对非线性相位产生的相位失真没有一个直观的认识。我们现通过一个例子，利用Matlab仿真来解释线性相位和非线性相位对于信号特性的影响[3]。

假设信号为y1(n)=sin(n)+sin(2n)，其波形如图1(a)所示。其中两条虚线分别表示两个频率分量sin(n)和sin(2n);粗实线表示的是两个分量的和，即信号sin(n)+sin(2n)。

若该信号通过一个线性相位的系统，则不同信号频率分量的相移与频率成正比，即如果分量sin(n)的相位滞后了φ1。那么分量sin(2n)将滞后2φ1，则输出信号为

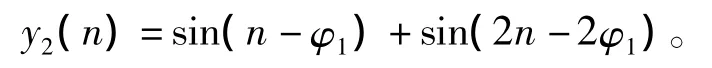
图1(c)和图1(d)分别给出了φ1=π和2π时的图形。从图上我们可以看出，这两幅图的波形和原始的波形一样，所不同的是其波形和原始波形之间相差一个相位π或2π。可见一旦系统具有线性相位，其合成输出信号波形就不会发生相位失真。

若该信号经过一个非线性相位的系统，由于非线性相位，信号的相移和频率不成正比，则如果分量sin(n)的相位滞后1.5π，而分量sin(2n)的相位可能滞后0.5π，则通过系统输出信号为

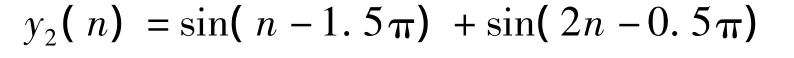
由图1(b)可以看出，合成的输出信号和原始信号相比，发生了明显的失真。

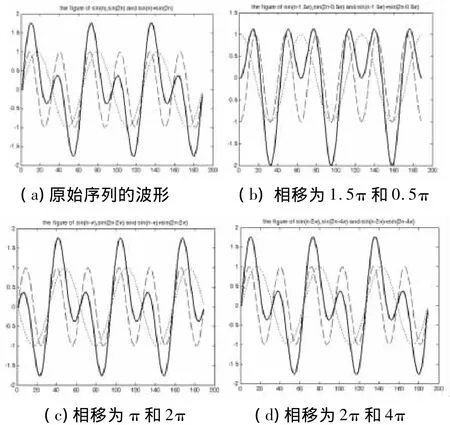
图1 信号经过不同系统后的波形比较

2 传统的线性相位的教学方法

传统的线性相位的教学方法，一般是根据序列信号h(n)的奇偶对称性推导出H(ejω)的结果，从而得出相频特性，其过程可以简述如下[4]。

当h(n)为中心偶对称时，通过理论推导可得

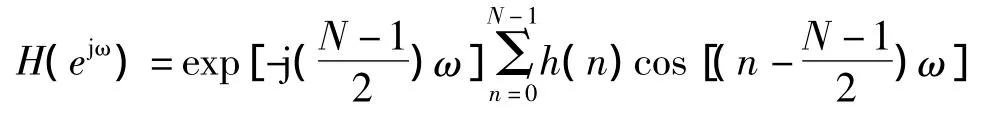
于是得到θ(ω)=-(N－1)ω/2。这就证明了一旦h(n)为中心偶对称，则具有第一类线性相位。

当h(n)为中心奇对称时，通过理论推导可得

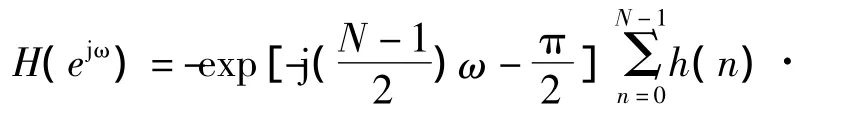
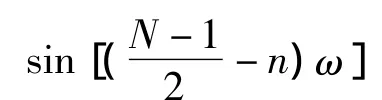
由此可以得到θ(ω)=-(N－1)ω/2－π/2。这就证明了一旦h(n)为中心奇对称，则具有第二类线性相位。

这种传统的教学方法主要依靠数学公式的推导，教师在讲解的过程中比较费劲，学生理解起来也比较困难。

3 新的线性相位的教学方法

下面我们提出一种利用序列的离散时间傅里叶变换(DTFT)的共轭对称特性来理解线性相位条件的教学方法。一个中心偶对称序列h(n)，可以看成是一个偶对称序列向右平移(N－1)/2单位，如图2所示。

图2 偶对称序列和中心偶对称序列

根据DTFT的共轭对称特性可知，一个序列可以分解为共轭对称分量和共轭反对称分量。其中，共轭对称分量的DTFT对应着原序列DTFT的实部，而共轭反对称分量的DTFT对应着原序列DTFT的虚部。由于一个偶对称序列的共轭反对称分量为0，因此偶对称序列的DTFT的虚部也就为0，因此偶对称序列的DTFT只有实部，因此一个偶对称序列的DTFT的相位为0。根据DTFT时移定理，可知移位之后的序列和原序列的DTFT的关系为

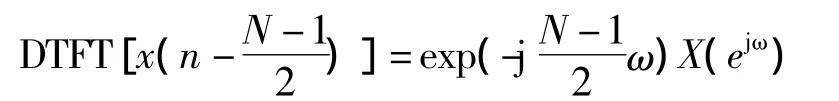
因此，中心偶对称序列的相频特性为θ(ω)=-(N －1)ω/2。

同理可知:一个中心奇对称的序列，可以看成是一奇对称的序列向右平移(N－1)/2个单位，如图3所示。

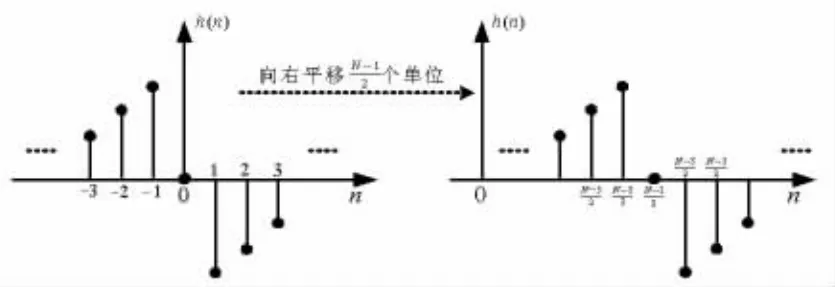
图3 奇对称序列和中心奇对称序列

由DTFT的共轭对称性可知，一个奇对称的序列的共轭对称分量为0，因此奇对称序列的DTFT的实部为0。因此奇对称序列的DTFT只有虚部。因此一个奇序列的DTFT的相位为－π/2。根据DTFT时移定理，可知中心奇对称序列的DTFT的相位特性为θ(ω)=-(N－1)ω/2－π/2。

这里我们利用以前所学过的DTFT的共轭对称性，说明了为什么中心偶对称的序列，具备第一类线性相位;为什么中心奇对称的序列具备第二类线性相位。这种方法相比于传统的公式推导法要简单明了，既便于学生记忆，达到了温故而知新的效果。

4 结语

本文通过一个例子利用Matlab仿真直观地解释了线性相位和非线性相位对信号特性的影响，随后提出了一种利用DTFT共轭对称性来帮助学生理解线性相位的方法。该方法不但能够避免复杂的数学推导，而且加深了学生对线性相位条件的理解。多年的教学实践表明，该方法具有较好的效果。

[1]徐以涛等.数字信号处理[M].西安:西安电子科技大学出版社，2009

[2]王玉德.“数字信号处理”课程的教与学的探讨[J].南京:电气电子教学学报，2008，30(6):97-98

[3]薛年喜.MATLAB在数字信号处理中的应用(第二版)[M].北京:清华大学出版社，2008

[4]胡广书.数字信号处理--理论、算法与实现[M].北京:清华大学出版社，2003