圆周卷积的竖式法求解分析

陈辉金，黄喜军

(桂林电子科技大学1.教学实践部;2.电子工程与自动化学院，广西 桂林 541004)

在“数字信号处理”课程中，一般是利用公式对圆周卷积进行求解的[1-3]。该方法虽然物理概念清晰但运算较复杂，费时又易出错。文献[4，5]中对竖式法求解卷积和进行了详细的讨论，该方法直观简便，且计算时采取“由左至右”与“由右至左”两种不同运算顺序，结果是一致的。笔者借鉴竖式法并稍作变化进行圆周卷积的计算，并就不同顺序时的运算结果进行了讨论。

1 公式法求解圆周卷积

以序列 x[n]={1，2，0，1}和 h[n]={2，2，1，1}(0≤n≤3)为例，运用圆周卷积的公式求解序列的4点圆周卷积。根据圆周卷积的定义:

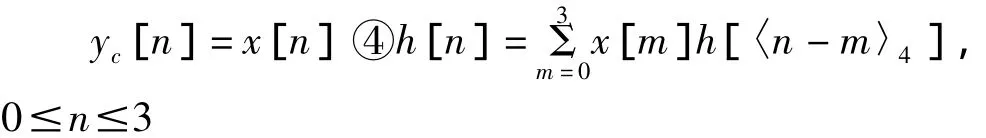
其中，h[〈n－m〉4]表示序列 h[n]的4 点圆周移位。

根据上式可得

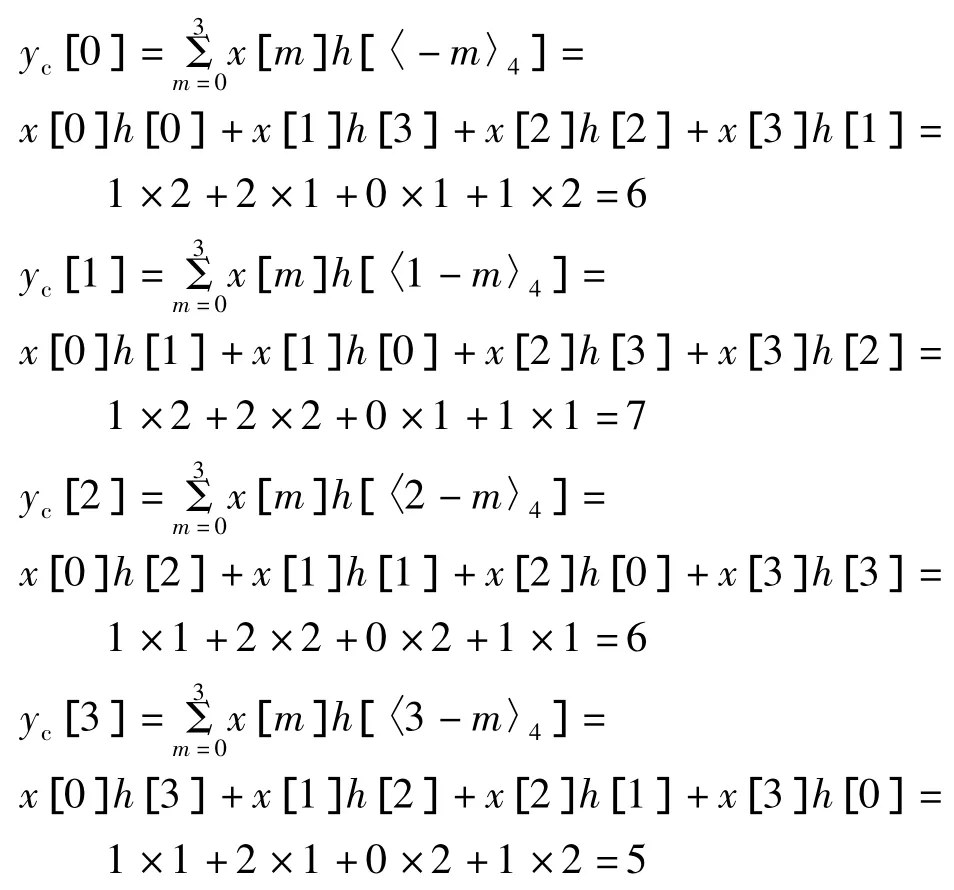
由此可得，x[n]和 h[n]的4点圆周卷积结果为 yc[n]={6，7，6，5}，0≤n≤3。从以上过程可以看出，圆周卷积的求解运算较复杂，也容易出错。

2 竖式法求解圆周卷积

2.1 按“由左至右”顺序求解圆周卷积

竖式法是将两个序列写成竖式相乘的形式，再进行相乘与相加运算，运算简便而不易出错。仍以上述序列为例，按“由左至右”顺序求解x[n]和h[n]的4点圆周卷积。

如图1所示，x[n]和 h[n]写成竖式相乘的形式，按“由左至右”顺序相乘，并注意对齐坐标。根据圆周移位的特点，将虚线以右部分的数据整体向左平移4位，即左侧三角框内的斜体数字为右侧三角框内的数字经平移4位得到，然后将虚线以左部分的数据相加，由此得到的圆周卷积结果为yc[n]={6，7，6，5}，0≤n≤3。这一结果与利用公式直接计算得到的结果一致。

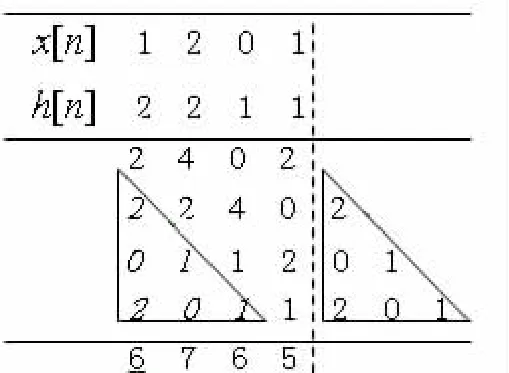
图1 坚式法“由左至右”求解圆周卷积

2.2 按“由右至左”顺序求解圆周卷积

这种求解方法如图2所示。先将x[n]和h[n]写成竖式相乘的形式，按“由右至左”顺序相乘。然后将虚线以左部分的数据整体向右平移4位。即图2中右侧三角框内的斜体数字为左侧三角框内的数字经平移4位得到。然后将虚线以右部分的数据相加，得到的圆周卷积结果为{5，6，7，6}，但此时对应的坐标n=3，0，1，2。也即序列须以第2个数据作为n=0时刻的值。

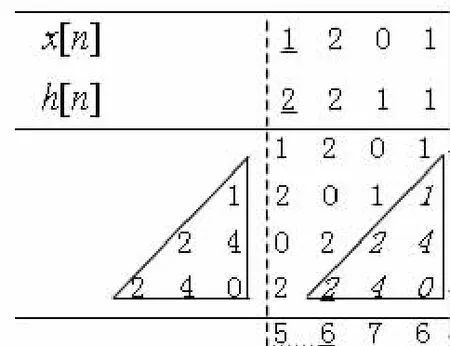
图2 竖式法“由右至左”求解圆周卷积

因为序列x[n]和 h[n]中 n=0时刻的值经相乘与平移操作后，对应于圆周卷积结果中的数字“6”，即为图2中带有下划线的数字。所以，按“由右至左”顺序求解x[n]和h[n]的4点圆周卷积结果仍为 yc[n]={6，7，6，5}，0≤n≤3。若直接把运算结果{5，6，7，6}作为圆周卷积的结果是不正确的，把运算结果按“由右至左”进行读取作为圆周卷积的结果也是不正确的。虽然此例中的数值结果似乎一致，换为其他数值进行运算，如将h[n]设为{1，2，3，1}进行计算，按“由右至左”进行读取的结果就不一致。所以，利用竖式法按“由右至左”顺序进行圆周卷积的计算时，不能简单地把运算结果按“由左至右”或“由右至左”进行读取作为圆周卷积的结果。

通过以上的求解过程可以看出，竖式法是求解圆周卷积的一种直观简便的方法，虽然两种顺序对应的结果看似不同，其实却是一致的，只需将“由右至左”获得的运算结果向左平移1位即可，只是此时的移位为圆周移位而已。当然，按“由左至右”的顺序进行运算的竖式法更易为初学者掌握。

3 结语

本文提出的用竖式法进行圆周卷积的计算，方法简单且不易出错。笔者对两种不同运算顺序的竖式法进行了讨论，得出按“由左至右”的顺序进行运算的竖式法更容易被初学者掌握的结论。当然，两个序列的圆周卷积满足一定条件时(即两序列长度之和减1以后小于等于圆周卷积的长度)，线性卷积与圆周卷积结果一致，而圆周卷积的计算可以通过FFT运算获得，所以最终可以通过FFT求出线性卷积。因此，在理解圆周卷积的作用后，不必在课堂教学中过多讨论圆周卷积的各种计算方法。

[1]陈后金，胡健，薛健.《数字信号处理》[M](第2版).北京:高等教育出版社，2008

[2]Sanjit K.Mitra.《Digital Signal Processing:A Computer-Based Approach》[M](Third Edition).BEIJING:Publish House of Electronics Industry，2006

[3]Vinay K.Ingle，John G.Prokis.《Digital Signal Processing Using MATLAB》[M].BEIJING:Science Press，2003

[4]黎明.探讨卷积和的求解方法[J].北京:北京工商大学学报，2005，23(2):49-51

[5]李昌利.有限长序列卷积和求解法[J].南京:电气电子教学学报，2008，30(1):45-47