传递函数的幅角定义探讨

陈凤祥，孙泽昌，赵治国

(同济大学汽车学院，新能源汽车工程中心，上海 201804)

0 引言

诸多经典自动控制原理的教材中对传递函数频率特性的幅角定义十分模糊甚至不准确，如教材[1]和教材[2]定义成

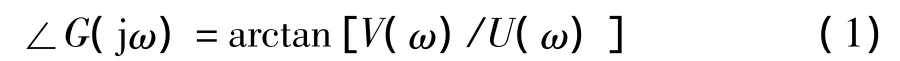
其中，G(jω)=U(ω)+jV(ω)

文献[3]尽管没有显式定义过幅角的具体形式，但是在公式的推导过程中也应用到了该结果。具体如下:

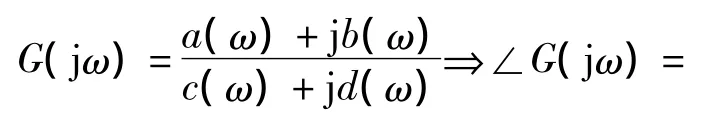
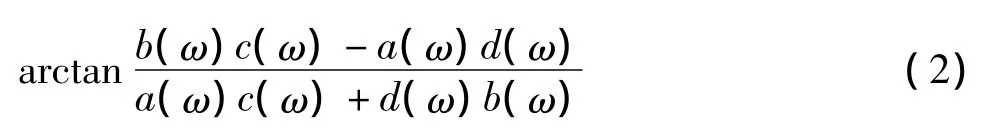
本文通过定义初探来分析这种定义的合理性。

1 定义初探

幅角y=arctan(x)的值域为(－π/2，π/2)，而∠G(jω)的值原则上至少在(－π，π)是没有任何限制的，显然式(1)的定义是存在缺陷的。

[例1]考察传递函数 G(jω)=1/(jTω －1)的Nyquist曲线:

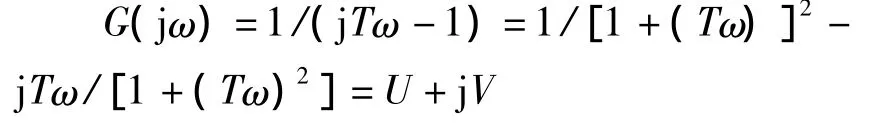
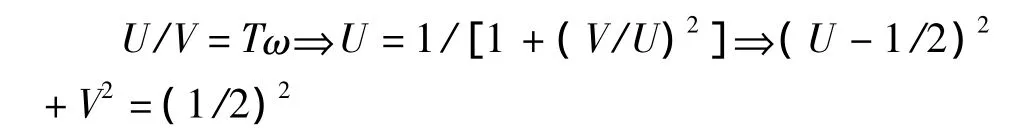
故曲线是位于图1所示的第三象限的半圆中。

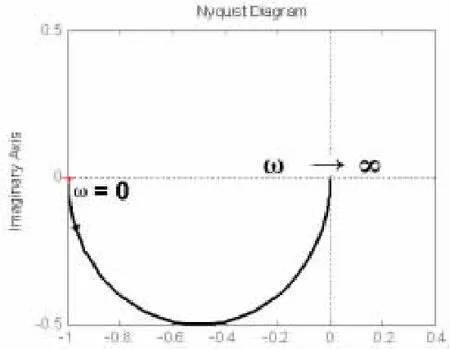
图1 1/(jTω－1)的Nyquist曲线

可见∠G(jω)∊(－π，－π/2)，若用式(1)则得

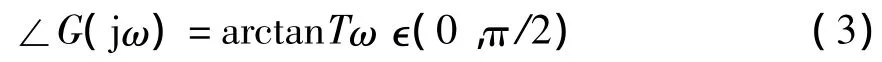
它显然不符上述结果。由图可知，正确的计算结果应该是

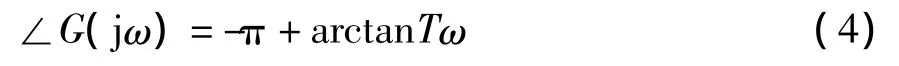
[例2]:求传递函数 G(jω)=1/(1+2ωj)(1+ ωj)的幅角

根据定义∠G(jω)=arctan[－3ω/(1 －2ω2)]∊(－π/2，π/2)，而实际上根据复数的乘法原理可以得到∠G(jω)= －arctan2ω －arctanω ∊(－π，0)。通过画Nyquist曲线，可以发现后者是正确的，前者是错误的。

既然这样的定义存在缺陷，又为何没有引起大家的正视呢?原因在于当G1(jω)=1/(jTω+1)或G2(jω)=jτω +1时，它的计算结果是正确的。因为，此时∠G1(jω)和∠G2(jω)正好落在(-π/2，π/2)范围内，也就是说当幅角落在(-π/2，π/2)时，定义式(1)的计算结果是正确的;另一方面，G(jω)=1/(jTω－1)是一个非最小相位系统。这样的系统往往在控制论入门级教材中，很少会在课堂上分析其相频特性和计算幅角。

对于高阶系统而言，由于其幅角并没有完全落在(-π/2，π/2)内，因此采用式(1)同样也是得不到正确的结果。但这些教材对于高阶系统的幅角求取的结果且是正确的:因为这些教材恰恰并未采用式(1)，而是利用复数的乘法原理以及传递函数为有理分式的性质进行了相关计算;而且，他们只对如下形式的传递函数幅角进行了计算:

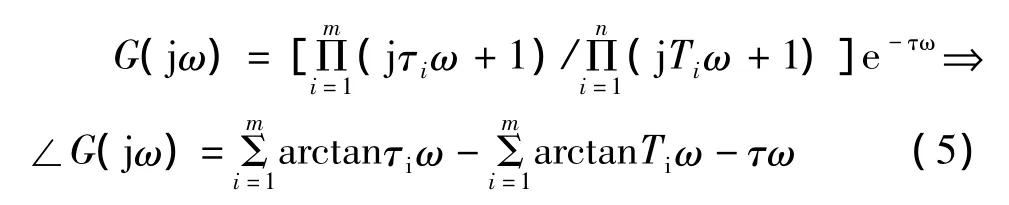
上述方法避开了式(1)定义的缺陷。但是从严密的角度而言，作为定义式(1)是需要被明确说明的，因为从式(1)我们无法得到式(5)这样的结果。另外，从课堂实际教学表明，自控专业的学生并不一定有扎实的复变函数知识，甚至某些专业的学生根本没有学过复变函数的课程，他们对复数的掌握还依然停留在高中时的那点基本知识。笔者曾经在未解释式(1)时，让学生求取G(jω)=1/(jTω－1)的幅角，最后发现50位上交作业的学生中，没有一个学生给出正确的结果。他们的解答几乎都采用了式(1)进行计算，从而得出∠G(jω)=arctanTω，这也就意味着这样的定义会误导学生，故需要被合理修正或额外的说明，否则容易造成误解。

2 定义说明

由于幅角本身是一个有无穷多个值，其中任意两个值相差的整数倍，而且幅角计算本身也比较复杂，很难给出简洁的计算公式[4]。因此，式(1)实际上只是一个形象公式，不能直接用来计算幅角。这是一种非常使人混淆的表述方式。因此，笔者认为教材不妨考虑用其它符号式来代替式(1)，来表达G(jω)的幅角:

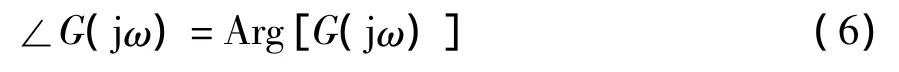
此外，考虑到经典控制论的传递函数多为一些有理分式

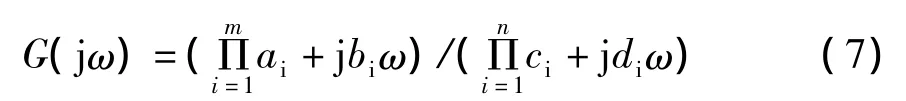
其中 ai，bi，ci，di∊R 。考虑到 ai+jbiω ，和 ci+jdiω的幅角值落在(－π，π)之间。因此，幅角计算公式可表述如下:

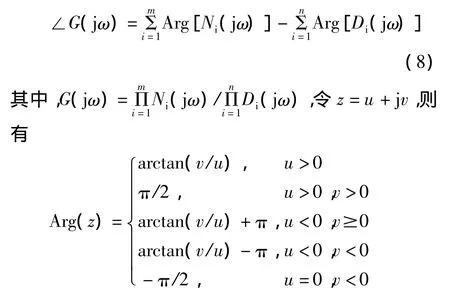
当传递函数中含有纯时滞环节，则式(8)可表述如下:

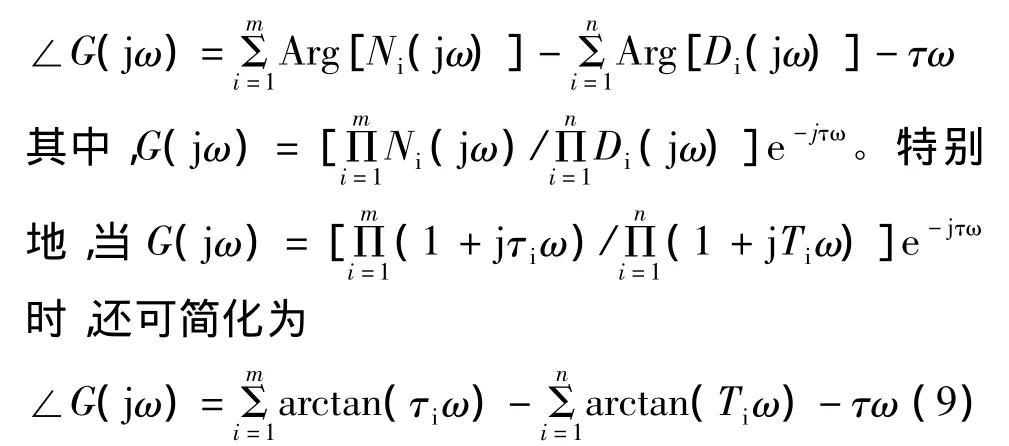
这就是现行教课书上所采用的计算方法。我们运用公式(8)可计算例一的幅角为∠1/(jTω－1)=－π+arctan(Tω)，即和式(4)完全相同。

3 结语

本文以G(jω)=1/(jTω－1)和二阶系统为例，分析了现存经典控制论教课书中传递函数幅角定义的缺陷，最后给出了一个较为完整的幅角定义修正想法和计算公式。虽然式(8)的计算公式比较复杂，不便记忆，但在实际运算时可通过数形结合的方式进行相关计算。

[1]孔祥东，王益群，控制工程基础(第3版)，北京:机械工业出版社，2008

[2]Richard C.Dorf Robert H.Bishop著，现代控制系统(第八版)，谢红卫，邹逢兴，张明，等译，北京:高等教育出版社，2001

[3]胡寿松，自动控制原理(第5版)，北京:科学出版社，2007

[4]李红，谢松法，复变函数与积分变换，北京:高等教育出版社，施普林格出版社，1999