圆柱形爆炸容器绝热剪切瞬态失效过程*

马 利，胡 洋，辛 健，郑津洋，邓贵德，陈勇军

(1.浙江大学化工机械研究所，浙江 杭州 310027;2.中国特种设备检测研究院，北京 100013;3.Institute of Reliable Legality of Components and Systems，University Karlsruhe(TH)，Karlsruhe 76128，Germany)

研究爆炸容器在内部强动载荷作用下的动力响应及其损伤与破坏机理是容器设计与安全使用的前提和基础。自20世纪60年代以来，有关爆炸容器的主要研究集中在爆炸流场、容器动力响应及设计方法等，而关于容器失效模式的理论和实验研究较少见。

在爆炸容器领域，目前一般使用最大薄膜应变来定义结构的塑性拉伸失稳失效。T.Nakamura等［1］提出在能量控制模式下，当结构出现塑性拉伸失稳失效时的环向薄膜应变大小分别为n(圆柱形爆炸容器)和2n/3(球形爆炸容器)，其中n为材料强化阶段的强化幂指数(见式σeff=)。而 T.A.Duffey等［2］得到的塑性拉伸失稳时所对应的环向薄膜应变为n(球形爆炸容器)。胡永乐等［3］在爆炸容器实验中也观察到塑性失稳和拉伸失效模式。需要指出的是现有的以薄膜应变是否达到阈值来判断爆炸容器是否失效，是沿用了结构的整体塑性失稳失效准则，但在高速冲击载荷下，结构往往表现为局部塑性失稳和剪切破坏，因此上述失效准则本身的适用性问题还值得进一步研究。

结构在高速冲击载荷下的剪切破坏已被证明与材料细观上的绝热剪切带有关，如M.A.Meyers等［4］、V.F.Nesterenko等［5］研究了圆柱形结构在内爆炸载荷作用下的 ASB 现象，D.M.Goto等［6］研究了爆炸载荷驱动下金属圆柱和圆环的断裂和碎片，发现裂纹沿绝热剪切带方向扩展，且在碎片中也发现存在绝热剪切带。胡八一等［7-8］开展了爆炸金属管绝热剪切断裂的宏细观研究，观察到爆炸金属管具有不同的细观剪切断裂机制，金相研究及物理分析表明，金属材料的热导率越低，颗粒越细，则越容易产生绝热剪切，生成相变带。

因此，本文中拟基于实验结果，提出爆炸容器以绝热剪切为主导的韧性失效模式。绝热剪切包含一系列微观结构和状态的转变，如晶粒的极度拉长、孔洞的生长和聚集等，直接模拟这些微结构的演化过程很困难，在数值上难以实现。但是通过建立绝热剪切损伤模型，将绝热剪切带不同演化阶段的临界状态与宏观的力学条件联系起来，并将这些力学临界条件作为动态失效准则引入到宏观计算程序中，从而可以基本模拟爆炸容器发生绝热剪切的的瞬态过程，并由此预测由绝热剪切所造成的容器破坏形貌。

1 爆炸容器逐级加载和破坏实验

图1是圆柱形爆炸容器实验装置示意图，高能炸药TNT被装入硬纸制成的圆管中，并悬挂放置在容器壳体纵向轴线中部。实验过程中，采用逐级装药方式，测试容器在不同爆炸载荷下的动力响应和破坏模式。加载分为6级，TNT装药量分别为20、55、250、425、500、600 g。容器经逐级装药加载后，最终在600 g TNT作用下的断裂破坏形貌如图2所示。

图1 圆柱形爆炸容器实验装置示意图Fig.1 Schematic diagram of cylindrical explosion containment vessel

由图2可见，爆炸容器在高速冲击载荷作用下，表现出明显的剪切破坏模式，断口与圆柱轴线成45°角，且断裂面与壁厚方向也成45°角。通过对破坏后容器的显微结构观测，发现这种剪切破坏与材料内部形成的绝热剪切带有一定的关联。图3是在裂纹尖端用光学显微镜观察的结果，在变形带两侧，晶粒颗粒粗大，形状保持完整，而在变形带内，晶粒被极度拉长和碎化。图4是裂纹前端的微孔洞和微裂纹，这是材料发生绝热剪切不同演化阶段的典型特征。

图2 爆炸容器破坏形貌Fig.2 Failuremode of vessel

图3 变形带Fig.3 Deformed band

图4 微孔洞和微裂纹Fig.4 Micro voids and cracks

2 绝热剪切损伤演化模型

受实验环境、测试设备等限制，在爆炸容器爆炸加载实验中实时地观测绝热剪切带的发展演化很困难。绝热剪切包含一系列微观结构和状态的转变，如晶粒的极度拉长、孔洞的生长和聚集等，直接模拟这些微结构的演化过程在数值上也难以实现。但是材料发生绝热剪切时，微结构和状态的改变实际上依赖于不同的力学条件，如果能够将这些不同演化阶段的临界状态与宏观的力学条件联系起来，并将这些力学临界条件作为动态失效准则引入到宏观计算程序中，则就抓住了剪切带传播演化的本质，就可以基本模拟爆炸容器发生绝热剪切的的瞬态过程。

M.Zhou等［9-10］针对绝热剪切失效模式提出了如下式所示的率相关失效准则

式中:ε1、ε2是经验参数，且ε1＜ε2，是参考应变率。M.Zhou等［9-10］建议ε1=4σ0/E，σ0是材料屈服强度，E是弹性模量，ε2=0.3。

实际上，王礼立等［11］在针对TC4钛合金绝热剪切的研究中，基于下式所示的热粘塑性本构方程

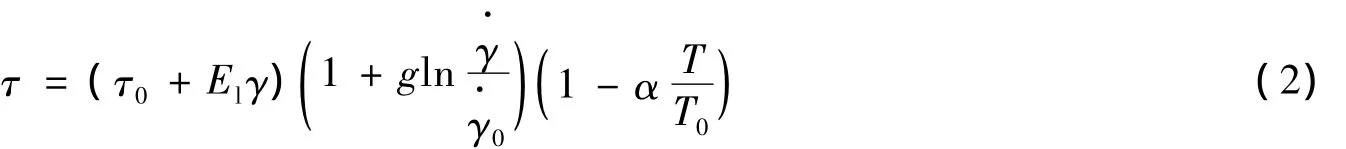
开展失稳分析，并得到了如下式所示的临界条件

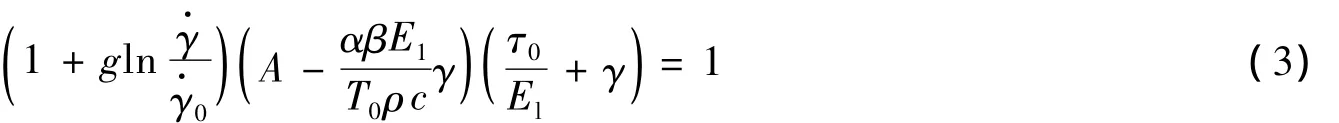
式中:τ为剪应力，γ为剪应变，El为线性应变硬化模量，g、α分别表征材料的应变率硬化和热软化特性。β是塑性功转化系数，一般取0.9～1.0。对应不同积分常数A，式(3)表征一族临界应变率-应变曲线，分别对应不同的绝热剪切阶段演化特征状态。

据此本文中提出了应变率-应变空间内的绝热剪切损伤演化模型，如图5所示。在剪切带形成阶段，认为它是一个相对“慢变”的过程，材料发生均匀变形，可采用热粘塑性本构方程。当材料达到失稳点后，则进入剪切带的传播阶段。传播阶段属于“快变”的过程，并包含相变、再结晶过程，一般应采用多物理本构模型描述该阶段的材料行为。剪切带内发生的应力突降被称为应力垮塌，此时可采用拟流体本构方程描述剪切带内材料的流动。当剪切带发展到最终阶段，则对应于微孔洞聚合形成微裂纹，材料彻底破坏。

具体的做法是在LS-DYNA等计算软件的基础上编写UMAT用户子程序，在瞬态分析的每个时间步，结合反映剪切带临界状态的曲线，判断节点落在哪一曲线范围，从而判断该点相应的微观形态，并对它作对应形态的标记，对满足流动法则的节点或单元赋予其剪切带内拟流体本构关系，并计算剪切带内材料的压力、温度和应变率，删除处在熔化、开裂状态的单元和节点。被删除的区域又将导致结构承载能力的弱化，引起附近区域应力、应变状态的改变。在每个时间步重复以上计算步骤，可以模拟剪切带的一系列阶段在结构中的演化过程。

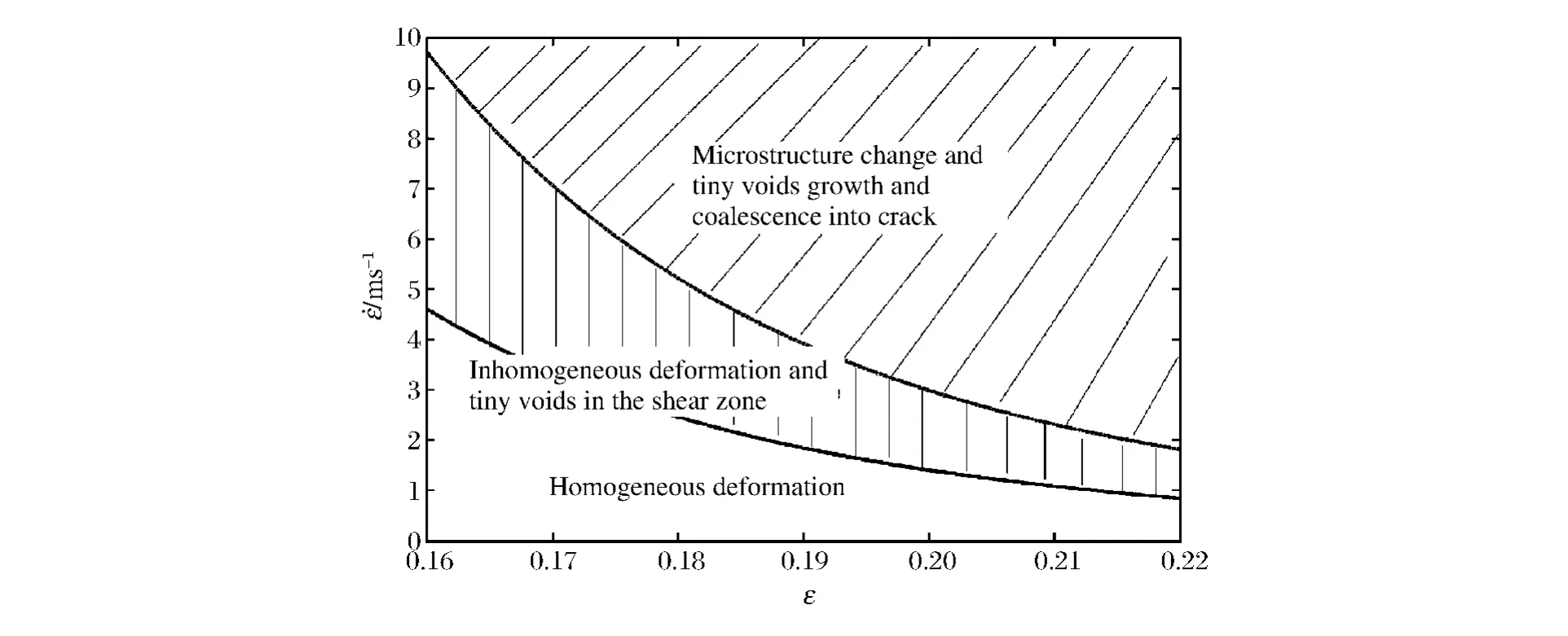
图5 应变率-应变空间内的绝热剪切损伤演化模型Fig.5 Adiabatic shearing failuremodel concluding strain and strain rate

3 绝热剪切瞬态失效过程数值模拟

3.1 计算模型

根据图1所示的容器结构尺寸建立计算模型，由于实验容器在实验过程中经受了历次的爆炸载荷直至最终破坏，本文中将之前多次加载的效果考虑成在爆心环面引起的微小缺陷。在容器的爆心内环面设置一个“十”字型的初始缺陷，该“十”字型的边长均为1 mm，深度为185μm。设置初始缺陷是为在此处产生应力集中，从而引发绝热剪切所造成的裂纹。选择“十”字型的目的是允许裂纹沿纵向或环向均有同等的被激发可能性，这样就可消除由于初始缺陷的方向性而导致裂纹传播方向上的偏离。基于邓贵德［12］关于爆炸容器壁面反射超压的讨论，为简化计算，此处采用解耦算法。即首先考虑炸药-空气-容器的流固耦合效应，计算得到作用在容器内壁面上的反射超压，然后在失效分析过程中将该压力作为载荷直接施加到含缺陷的容器结构上。

计算中采用3维8节点单元，在缺陷周围的最小网格尺寸控制为74μm，而远离缺陷处的壳体远场范围网格尺寸控制为2 mm。材料模型采用45钢的Jonson-Cook本构模型［13］。目前计算中仅采用了图5中微孔洞聚集并产生微裂纹时所对应的应变率-应变临界条件，将满足条件的单元直接删除，被删除的单元所组成的轨迹则近似于由绝热剪切带所导致的裂纹在爆炸容器上的扩展途径。

3.2 结果分析

图6是容器在不同时刻的失效过程模拟。在95μs时，一个微小的裂纹开始贯穿壁面，在105μs时，裂纹扩展速度明显加快，并且产生分岔。在150μs时，裂纹分岔更加明显，并且容器壁面形成一个“X”形的断口，见图6(d)。比较图2与图6可见，数值模拟结果与实验结果具有良好的一致性。但是必须承认二者之间仍存在一定的差异，实际容器的断裂形貌特征尺寸和翘曲程度明显高于数值计算结果。引起这种差异的2个主要原因为:一是数值计算中采用了解耦算法，而实验中一旦容器壁面出现穿透裂纹，内部的高压气体会立即从裂纹口中释放，对断裂面会产生扩孔效应;二是目前的数值计算仅考虑满足极端条件时，材料发生断裂，而实际上在材料断裂之前，由于温升软化导致局部区域材料发生大的流动和剪切变形，这一点在目前的计算中还未考虑。

同样，本文中还进行了一系列的计算，以确定失效准则和初始缺陷对最终失效模式的影响。图7是在相同的载荷条件和缺陷类型的情况下，采用较低的临界失效应变εf=0.25得到的计算结果。需要指出的是，关于爆炸容器的失效应变目前并没有一个明确的取值，因而参考文献［14］，暂取0.25.计算时间总计为250μs，这个时间范围已足够满足裂纹的充分扩展。但是，计算结果表明，在静态失效应变下，裂纹扩展速度较慢，直至142μs时，裂纹仍未贯穿容器壁面，同时，裂纹主要沿筒体纵向扩展，没有出现分岔，与实验结果明显不符。

图6 模拟的爆炸容器绝热剪切失效过程Fig.6 Simulated adiabatic shearing failure process

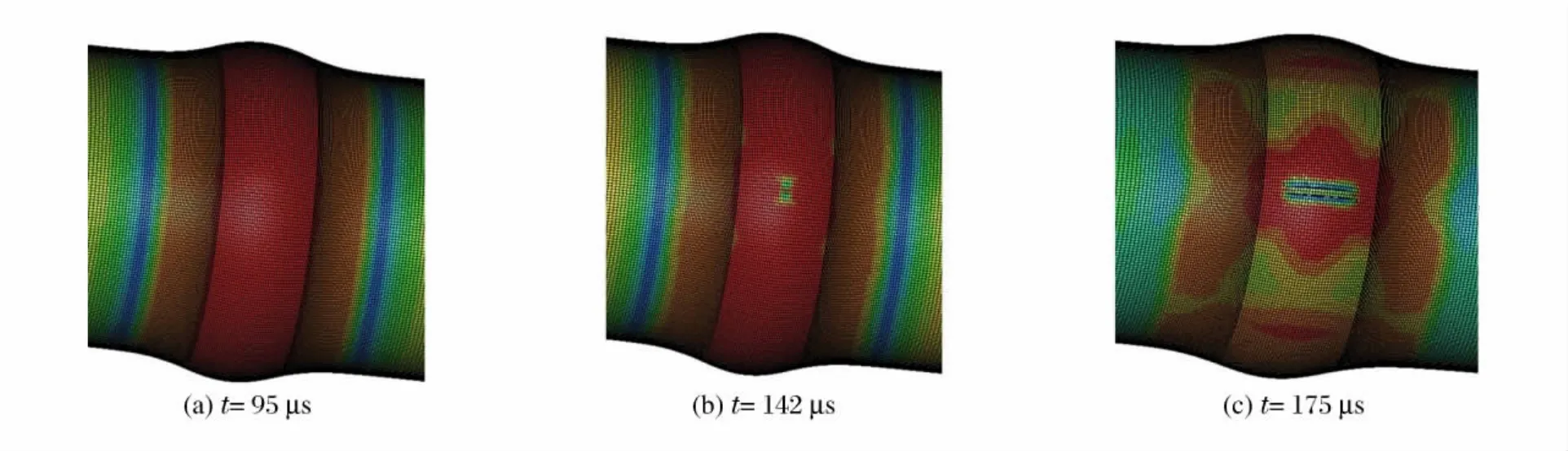
图7 静态失效准则控制下的失效过程Fig.7 Failure process with constant failure strain

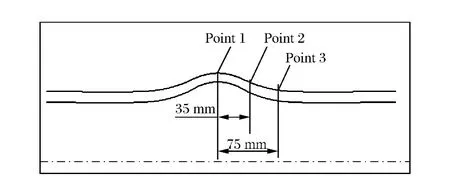
图8 远离裂纹扩展区域的位置示意图Fig.8 Locations away from structural discontinuities

计算还表明，2种不同失效准则模型的差异主要表现在裂纹扩展的邻近区域内。在远离裂纹扩展区域，结构的动力响应很接近。图8是远离裂纹扩展区域的点1、2、3位置示意图。图9是在2种失效准则下的径向位移s，从图中可以看出二者符合较好。

由于裂纹在扩展过程中出现分岔，以至无法用裂纹长度对时间的导数来表征裂纹扩展速度，这里采用质量损失md来表征裂纹扩展程度，如图10所示，在动态失效准则下，容器质量损失约是静态失效准则结果的3倍。在动态失效准则下，质量损失下降曲线较尖锐，这说明裂纹扩展速度较快。而在塑性应变失效准则下，容器一开始并未产生质量损失，直至达到预设的失效应变时，裂纹才开始扩展，扩展速度较慢，并在200μs时停止了扩展。

本文中也考虑了不同初始缺陷对容器失效模式的影响。分别改变“十”字形初始缺陷的环向和轴向长度，计算了环向长度为0.5mm、轴向长度为1 mm，以及环向长度为1 mm、轴向长度为0.5mm的情况下，容器的失效模式。计算结果与图6所示的断裂形貌很接近，仅在特征尺寸上有较小的差异。该计算结果说明，对于一定的爆炸载荷，容器的剪切失效模式主要由率相关的动态失效准则控制，设置初始缺陷的主要作用是激发绝热剪切的产生，对容器最终破坏模式的影响较小。

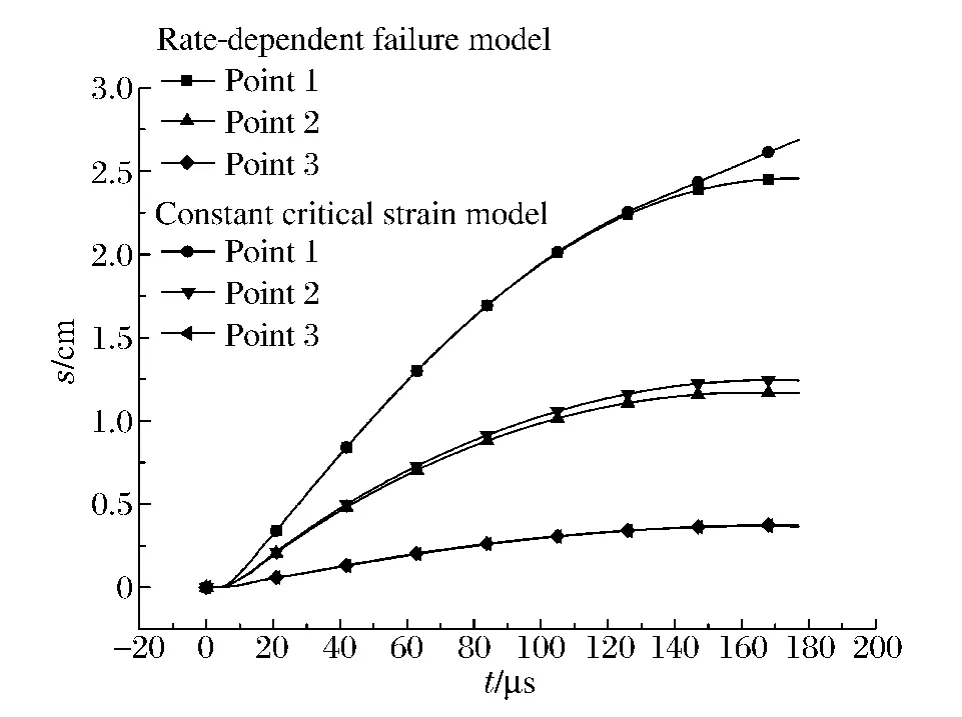
图9 对应图8中的各点的径向位移Fig.9 Radial displacement corresponding to the three points in Fig.8

图10 质量损失Fig.10 Mass loss

4结论

开展了圆柱形爆炸容器逐级加载和破坏实验，基于破坏后容器的剪切断裂模式和光学显微检测，证实了绝热剪切是导致爆炸容器失效的一种机制。以往绝热剪切带的研究以实验为主，而本文中通过建立绝热剪切损伤演化模型，实现了爆炸容器在绝热剪切损伤机理作用下的裂纹瞬态扩展过程模拟，模拟结果近似预测了爆炸容器最终的断裂形貌。数值模拟结果还表明，爆炸载荷和率相关失效准则是控制绝热剪切失效模式的2个主要因素，细观初始缺陷往往导致绝热剪切的激发，但对容器最终的失效模式的影响是次要的。当容器在爆炸载荷作用下发生绝热剪切破坏模式时，裂纹(剪切带)扩展速度较快，此时若仍采用整体塑性应变失效准则考察容器的动力响应并作为失效判据，将不能预见材料局部的弱化和破坏。以上认识对于爆炸容器设计以及在役容器寿命评估具有重要意义。

［1］Nakamura T，Kaguchi H，Kubo S.Failure strain of thin cylindrical vessel subjected to dynamic internal pressure［C］∥Baliga R.Proceedings of the 2000 ASME Pressure Vessels and Piping Division Conference.2000:47-54.

［2］Duffey T A，Doyle D.Plastic instabilities in spherical shells under load，displacement，and impulsive loading［C］∥Proceedings of the 2006 ASME Pressure Vessels and Piping Division Conference.Vancoucer，BC，Canada，2006:99-110.

［3］胡永乐，喻名德，崔云霄.爆炸容器塑性失稳和变形吸能［C］∥黄风雷，张庆明.第九届全国冲击动力学学术会议论文集.北京:北京理工大学，2009:160-164.

［4］Meyers M A，Wang SL.An improved method for shock consolidation of powders［J］.Acta Metallurgica，1988，36(4):925-936.

［5］Nesterenko V F，Bondar M P.Localization of deformation in collapse of a thick-walled cylinder［J］.Combustion，Explosion，and Shock Waves，1994，30(4):500-509.

［6］Goto D M，Becker R，Orzechowski T J，et al.Investigation of the fracture and fragmentation of explosively driven rings and cylinders［J］.International Journal of Impact Engineering，2008，35(12):1547-1556.

［7］胡八一，董庆东，韩长生，等.爆炸金属管的绝热剪切断裂宏观研究［J］.爆炸与冲击，1992，12(4):319-325.

HU Bai-yi，DONG Qing-dong，HAN Chang-sheng，etal.Themacroscopic study of adiabatic shear fracture ofmetal tubes under explosive loading［J］.Explosion and Shock Waves，1992，12(4):319-325.

［8］胡八一，董庆东，韩长生，等.爆炸金属管绝热剪切断裂的细观研究［J］.爆炸与冲击，1993，13(4):305-312.

HU Bai-yi，DONG Qing-dong，HAN Chang-sheng，et al.Mesoscopic study of adiabatic shear fracture of themetal tubes under internal explosive loading［J］.Explosion and Shock Waves，1993，13(4):305-312.

［9］Zhou M，Rosakis A J，Ravichandran G.Dynamically propagating shear bands in impact loaded prenotched plates(I):Experimental investigation of temperature signatures and propagation speed［J］.Journal of the Mechanics and Physics of Solids，1996，44(6):981-1006.

［10］Zhou M，Ravichandran G，Rosakis A J.Dynamically propagating shear bands in impact loaded prenotched plates(II):Numerical simulations［J］.Journal of Mechanics and Physics of Solids，1996，44:1007-1032.

［11］王礼立，余同希，李永池.冲击动力学进展［M］.合肥:中国科学技术大学出版社，1992:1-33.

［12］邓贵德.离散多层爆炸容器内爆载荷和抗爆特性研究［D］.杭州:浙江大学，2008:61-72.

［13］胡昌明，贺红亮，胡时胜.45号钢的动态力学性能研究［J］.爆炸与冲击，2003，23(2):188-192.

HU Chang-mimg，HE Hong-liang，HU Shi-sheng.A study on dynamicmechanical behaviors of 45 steel［J］.Explosion and Shock Waves，2003，23(2):188-192.