环形激波聚焦流场特性的数值研究＊

陈二云，赵改平，杨爱玲

（1.上海理工大学能源与动力工程学院，上海 200093；2.上海理工大学医疗器械学院，上海 200093）

激波聚焦［1］是指在一定条件下激波在其传播方向上发生收敛的行为。激波聚焦产生的瞬态高温高压脉冲在工程技术领域具有重要的应用价值，如第一台体外激波粉碎肾结石的新型医疗机械就利用了激波聚焦过程产生高能密度的力学特性。激波聚焦的一种简单实现方法是让平面入射激波在凹形壁面反射实现聚焦。而环形激波聚焦不需要反射物面，具有三维会聚的特点，能获得更好的聚焦效果［2］。

激波聚焦的研究方法主要有理论分析、实验测试和数值模拟。T.Satio［3］从理论、计算和实验等3个不同的角度对半球形弱冲击波的聚焦问题进行了研究。S.Hamid等［4］利用无膜激波管对低马赫数环形激波在激波管内的聚焦情况进行了实验研究，获得了流场在不同时刻的全息干涉条纹和壁面各点压力时程曲线。对于高马赫数下环形激波聚焦实验测试技术比较困难，因此数值模拟是一种较好的研究手段。目前，对于此类流动的数值模拟方法主要有DCD［5］、FVM［6］和 WENO［7］格式，能够较好的模拟出激波聚焦过程中的复杂流场结构。但这些方法都必须通过扩大节点模板来提高解的精度，因此在求解包含复杂几何外形的流动问题时，不利于程序的编制和边界条件的处理。

B.Cockburn等［8］、J.Qiu等［9］、N.Chevaugeon［10］提出了一种间断有限元方法。该方法吸收了有限元方法和有限体积方法的优点，具有一致高阶精度、网格适应性强、结构守恒性和容易向高维推广等特点。与其它方法相比，该方法最大的优点在于解的精度是通过提高插值多项式的阶数来实现，无需扩大节点模板，便于程序的编制和边界条件的处理。

本文中，在已有工作的基础上，采用间断有限元方法模拟了环形激波在同轴圆柱形激波管内的聚焦流场特性，分析环形管道内外半径对聚焦峰值压力的影响作用。计算的结果可以为实际的工程应用提供一定的理论指导。

1 间断有限元方法

1.1 控制方程

忽略粘性和热传导效应的假设下，轴对称Euler方程组表示为

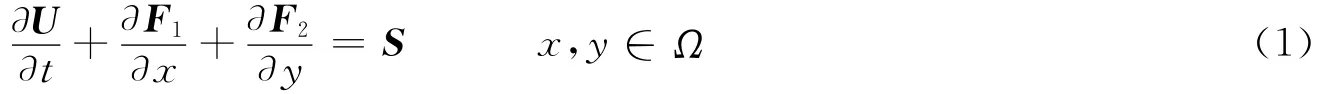
式中：U＝，t是时间变量，ρ是密度，u和v分别为对应于x和y方向的速度分量，p是压强，E＝ρe＋ρ（u2＋v2）／2，表示单位体积的总能量，e是单位质量内能，对于完全气体，状态方程p＝（γ－1）ρe，γ是比热容比。

1.2 数值离散

在数值模拟中，对式（1）的空间离散形式采用间断有限元方法。设Γh是区域Ω的一个有限剖分，单元K∈Γh，∂K表示单元K的边界，n表示单元边界的外法向。将间断有限元的局部解空间定义为单元上次数不超过2的多项式集合，记为V（K）。对于任意时刻t，在间断有限元空间Vh＝中寻找近似解Uh（X，t），其中X＝（x，y）。

首先在单元K上用连续函数vh∈Vh乘式（1）的两端，并用他的近似解Uh（X，t）∈Vh代替式（1）中的精确解U（X，t），由Green公式，得

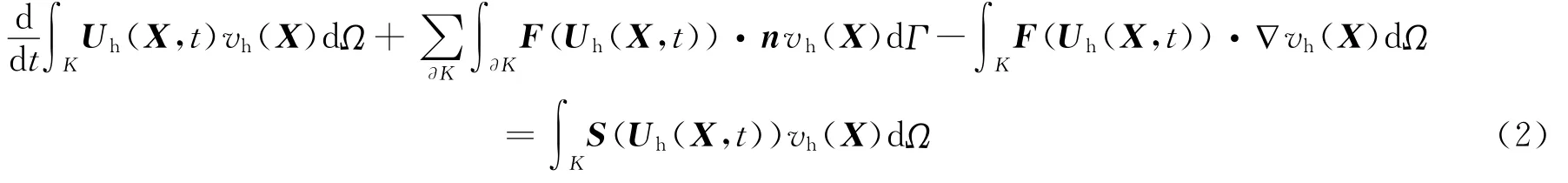
式中：F＝，用数值通量H（X，t）代替通量F（Uh（X，t））·n，得

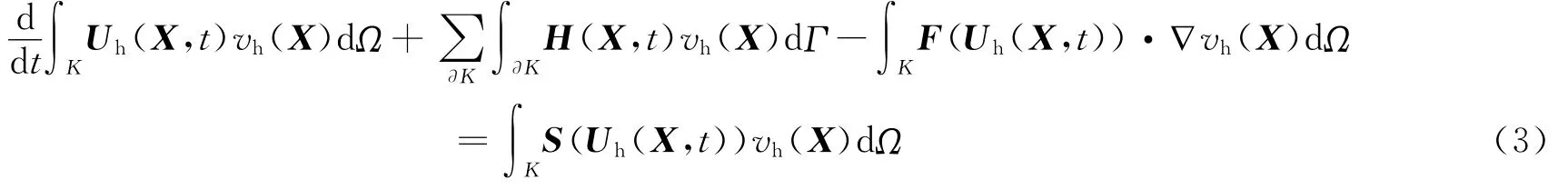
数值通量定义为H（X，t）＝H（Uh（Xint（K），t），Uh（Xext（K），t）），体现了与相邻单元之间的信息传递，同时也保证了离散格式的守恒性。

式（3）中的积分用数值积分代替

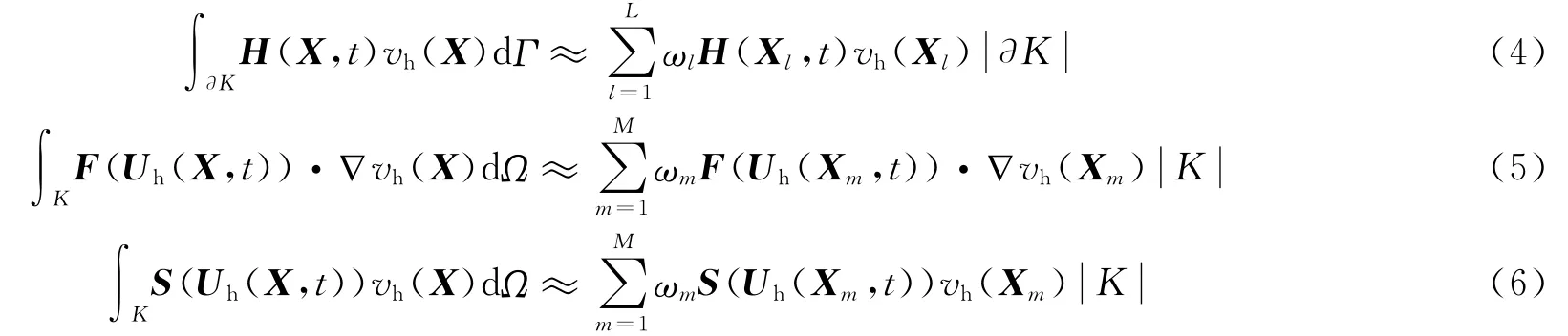
最后得到弱表达式

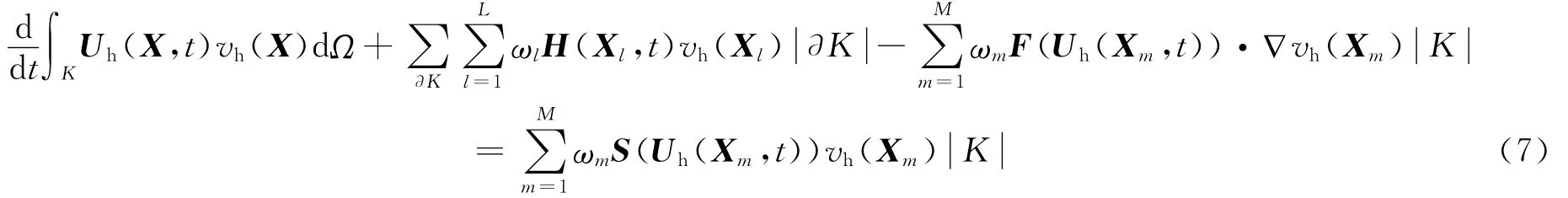
为了计算的方便，在单元K中取正交基函数（如勒让得多项式）｛φ1，φ2，φ3，…，φj｝，则质量矩阵成为分块对角矩阵，故有限元解可以表示为

令式（7）中vh（X）＝φi（X），得

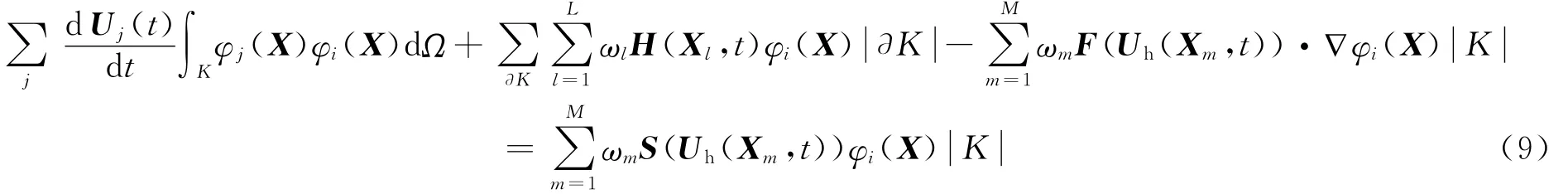
设MK为单元K的质量矩阵，则vh∈V（K），∀K∈Γh，式（9）可写成常微分方程形式

式中：算子Lh表示对（－∇·F＋S）的近似离散，γh为迹函数。在时间推进方面，为了与空间离散保持一致高阶精度，采用三阶Runge－Kutta时间离散形式［8］。

2 计算结果与分析

计算区域如图1所示，其中L表示圆柱形激波管半径，D与d分别表示环形管道的内外半径。初始时刻，马赫数为3.0的环形激波从环形管道向同轴圆柱形管道传播，波前气体处于静止状态，网格步长Δx＝Δy＝1／500。

图2给出了当L∶D∶d＝1∶0.4∶0.2时，环形激波从环形管道向同轴圆柱形管道传播过程的压力等值线分布。

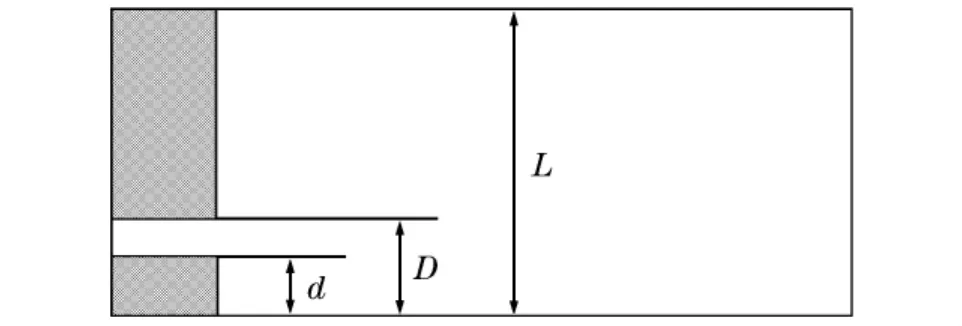
图1 计算区域示意图Fig.1Computation domain

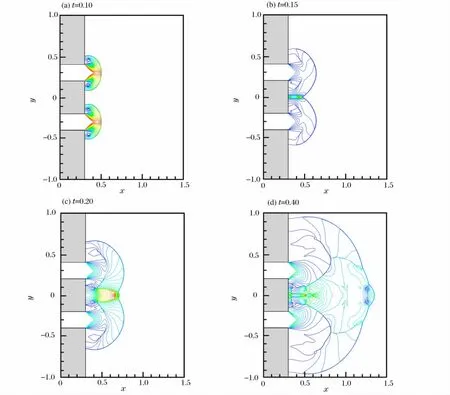
图2 压力等值线分布 （Ma＝3.0）Fig.2Distributions of pressure contours（Ma＝3.0）

从图中可以看出，当激波进入圆柱形管道后，由于传播截面突然增大，激波发生绕射，绕射波在台阶拐角处产生2个很强的漩涡，如图2（a）所示。当绕射激波到达对称轴时，激波聚焦在对称轴上，在聚焦点附近形成局部的高温高压区域，且在漩涡附近出现了二次激波，同时激波在对称轴上发生由规则反射向马赫反射的转变，如图2（b）所示。激波在对称轴上发生马赫反射之后，马赫杆受到激波聚焦诱发的强射流冲击作用，再次发生马赫反射，使得马赫杆向前凸起呈半球面形状，并且与原马赫杆相交位置形成三波交点，如图2（c）所示。随着时间的进一步发展，对称轴附近的球面状马赫杆继续凸起，前端已经超越绕射激波的波阵面，后方有1个明显的漩涡，如图2（d）所示，这种激波结构又被称为球面双马赫反射，是环形激波聚焦过程中产生的典型流场结构。

图3（a）～（c）分别给出了L∶D∶d＝1∶0.4∶0.2，L∶D∶d＝1∶0.5∶0.2和L∶D∶d＝1∶0.5∶0.3，环形激波从环形管道向同轴圆柱形管道传播过程中的压力等值线分布。从图中可以看出，3种不同计算工况下捕捉到的流场结构特点（包括漩涡、二次激波、三波交点和球面双马赫反射等）基本是相似的，但也存在一定的差异。比较图3（a）和图3（b）可以发现，外侧台阶后面漩涡的位置随着环形管道外径的增大沿径向外移，靠近中心台阶后面的流场结构非常相似，当x＞0.5时，图3（b）中高压区域的覆盖面积明显增大。比较图3（b）和图3（c）可以发现，中心台阶后面的流场结构具有较大差别，随着环形激波管内径变大，环形激波在中心轴线的聚焦点向下游偏移，高压区域也相应地向下游偏移。

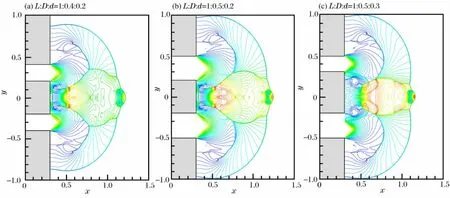
图3 压力等值线分布 （Ma＝3.0，t＝0.35）Fig.3Distributions of pressure contours（Ma＝3.0，t＝0.35）

图4（a）给出了L∶D∶d＝1∶0.4∶0.2和L∶D∶d＝1∶0.5∶0.2的情况下，环形激波在整个传播过程中轴线各点所能达到的最大压力分布曲线对比图，其中圆圈代表L∶D∶d＝1∶0.5∶0.2时轴线各点最大压力分布曲线，实线代表L∶D∶d＝1∶0.4∶0.2时轴线各点最大压力分布曲线，pmax／p0表示中心轴线上各点最大压力与环境静压之比。从图4（a）中可以看出，其它流动条件不变时，环形激波管外径对中心轴线各点最大压力值几乎没有影响，仅在下游较远位置二者有一定的差别。

图4（b）给出了L∶D∶d＝1∶0.5∶0.2和L∶D∶d＝1∶0.5∶0.3情况下，环形激波在整个流动过程中轴线各点所能达到的最大压力分布曲线对比图，其中圆圈代表L∶D∶d＝1∶0.5∶0.2时轴线各点最大压力分布曲线，实线代表L∶D∶d＝1∶0.5∶0.3时轴线各点最大压力分布曲线。从图4（b）中可以看出，在其他流动条件不变时，环形管道内径的增大使环形激波管中心轴线上绝大部分位置的最大压力都有一定增加，最大峰值压力pmax为约105p0，增加了约1.25倍，峰值压力位置也向下游偏移。

图4（c）给出了L∶D∶d＝1∶0.4∶0.2和L∶D∶d＝1∶0.5∶0.3情况下，环形激波在整个流动过程中轴线上各点所能达到的最大压力分布曲线对比图，其中圆圈代表L∶D∶d＝1∶0.4∶0.2时轴线上各点最大压力分布曲线，实线代表L∶D∶d＝1∶0.5∶0.3时轴线上各点最大压力分布曲线。从图4（c）中可以看出，中心轴线上各点最大压力的分布曲线与图4（b）相似，由此可知，环形激波在圆柱形管道内传播时，中心轴线上各点最大压力值受环形管道外径的影响较小，受环形管道内径的影响较大。

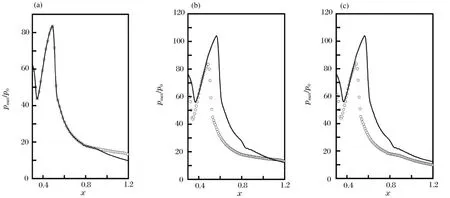
图4 中心轴线最大压力分布曲线 （Ma＝3.0）Fig.4Distributions of maximum pressure along the axis（Ma＝3.0）

3 结 论

采用三阶间断有限元方法对环形激波在圆柱形激波管内聚焦流场进行数值模拟。结果表明，三阶间断有限元方法能够较准确的捕捉到激波聚焦过程中复杂流场波系结构，通过改变环形管道内外半径对聚焦流场进行研究发现，环形激波在圆柱形管道内传播时，中心轴线上各点处最大压力值受环形管道外径的影响较小，受环形管道内径的影响较大。此外，环形激波在中心轴线上的聚焦位置随环形管道内径的增加向下游移动。计算结果可以为实际的工程应用提供一定的理论指导。

［1］董刚，叶经方，范宝春.激波聚焦反射的实验和数值研究［J］.高压物理学报，2006，20（4）：359－365.

DONG Gang，YE Jing－fang，FAN Bao－chun.Experimental and numerical investigation of shock wave focusing and reflection［J］.Chinese Journal of High Pressure Physics，2006，20（4）：359－365.

［2］TENG Hong－hui，JIANG Zong－lin.Gasdynamic characteristics of toroidal shock and detonation wave converging［J］.Science in China Series G：Physics Mechanics and Astronomy，2005，48（2）：739－749.

［3］Satio T.An experimental analytical and numerical study of temperatures near hemispherical implosion foci［R］.UTIAS Report No.260，1982.

［4］Hamid S，Hosseini R，Takayama K.Study of shock wave focusing and reflection over symmetrical axis of a compact vertical co－axial diaphragmless shock tube［C］∥Proceedings of ISSW23，2001：1550－1557.

［5］滕宏辉，姜宗林，韩肇元.环形激波绕射、反射和聚焦的数值模拟研究［J］.力学学报，2004，36（1）：9－15.

TENG Hong－hui，JIANG Zong－lin，HAN Zhao－yuan.Numerical investigation of diffraction，focusing and reflection of toroidal shock waves［J］.Acta Mechanica Sinica，2004，36（1）：9－15.

［6］滕宏辉，张德良，李辉煌，等.用环形激波聚焦实现爆轰波直接起爆的数值模拟［J］.爆炸与冲击，2005，25（6）：512－518.

TENG Hong－hui，ZHANG De－liang，LI Hui－huang，et al.Numerical investigation of detonation direct initiation induced by toroidal shock wave focusing［J］.Explosion and Shock Waves，2005，25（6）：512－518.

［7］Liang S M，Wu L N，Hsu R L.Numerical investigation of axisymmetric shock wave focusing over paraboloidial reflectors［J］.Shock Waves，1999，9（6）：367－379.

［8］Cockburn B，Shu C W.Runge－Kutta discontinuous galerkin methods for convection－dominated problems［J］.Journal of Scientific Computing，2001，16（3）：173－261.

［9］Qiu J X，Khoo B C，Shu C W.A numerical study for the performance of the Runge－Kutta discontinuous galerkin method based on different numerical fluxes［J］.Journal of Computational Physics，2006，212（2）：540－565.

［10］Chevaugeon N，Xin J，Hu P，et al.Discontinuous galerkin methods applied to shock and blast problems［J］.Journal of Scientific Computing，2005，22－23（1／2／3）：227－243.