钝感炸药点火增长模型的欧拉数值模拟＊

郝鹏程，冯其京，洪 滔，王言金

（1.北京应用物理与计算数学研究所，北京 100094；2.中国工程物理研究院研究生部，北京 100088）

塑性炸药的爆轰机理很复杂，对爆轰波结构的研究，早在一个多世纪以前就提出了平面、定常的CJ爆轰模型，即认为爆轰波由前导冲击波及紧跟的稀疏波构成，能量在冲击波后瞬间释放；ZND模型则在前导冲击波后引入化学反应区［1］。实际上，炸药内部微观结构复杂，由大量晶粒以及塑性粘结剂、缺陷、气孔等构成，在化学反应区内存在复杂的作用机制。现今大多认为，当炸药受到强烈冲击，由于摩擦、空洞塌陷、剪切带的形成和局部塑性变形等，使炸药局部急剧升温，即所谓的热点形成，消耗部分炸药，进而引发周围炸药点火起爆连成一片，在化学反应区内炸药逐渐转化为产物。在这一物理图景下，提出了许多唯象反应率模型，如JTF模型［2］、HVRB模型［3］、点火增长模型［4－5］和统计热点模型［6］等。在这些模型中，引入产物质量分额的概念，反应区内的炸药为反应物与产物的混合物，在一定假设之下得到混合物的状态。点火增长模型被广泛应用于模拟各种爆轰以及炸药与惰性材料的相互作用等现象。

唯象反应率模型从较简单的物理特征出发，常被推广应用于复杂的爆轰状况下，如炸药直径效应的模拟，也能得到令人满意的结果。凝聚炸药存在减敏现象，即受到弱冲击的钝感炸药与未受冲击的炸药相比，起爆炸药需要更强的冲击压力，并且，这一效应是与时间相关的过程［7］。当爆轰波遇到球形发散或拐角时，出现全部或部分炸药未被起爆的区域［8］，形成死区。单纯的反应率模型不能很好地模拟这一现象，特别是当爆轰波达到拐角后，由于稀疏效应压力减弱，无法起爆拐角后的炸药，但当爆轰波绕过拐角，压力增强会引爆先前未爆的炸药，先前形成的死区逐渐消失；引入减敏模型［9］后，模拟结果与实验现象接近。

自主研发的多介质欧拉弹塑性流体力学程序（Multicomponent Eulerian elastic－plastic hydrodynamics code，MEPH2Y）能有效地模拟流体、弹塑性介质高速碰撞等问题［10］，并行网格自适应加密（A－daptive mesh refinement，AMR）技术有效地扩展了MEPH2Y的适用范围［11］。为了研究钝感炸药的各种爆轰现象，本文中拟在MEPH2Y中加入反应进程变量和减敏进程变量的控制方程，通过对钝感炸药的平面爆轰波传播、直径效应和死区形成等爆轰现象的数值模拟，验证该程序用于研究钝感炸药的适用性和可靠性。

1 计算方法

1.1 控制方程

为了模拟钝感炸药的各种爆轰现象，在弹塑性流体力学控制方程中，引入炸药反应率和减敏模型，即加入反应进程变量F和减敏进程变量ψ的控制方程

式中：t为时间；SF和Sψ分别为与F和ψ对应的源项，F和ψ在0～1之间；F＝1，表示炸药均为产物；ψ＝1，表示炸药敏感性最低。式（1）右端的反应率源项SF采用三项点火增长反应率模型［5］

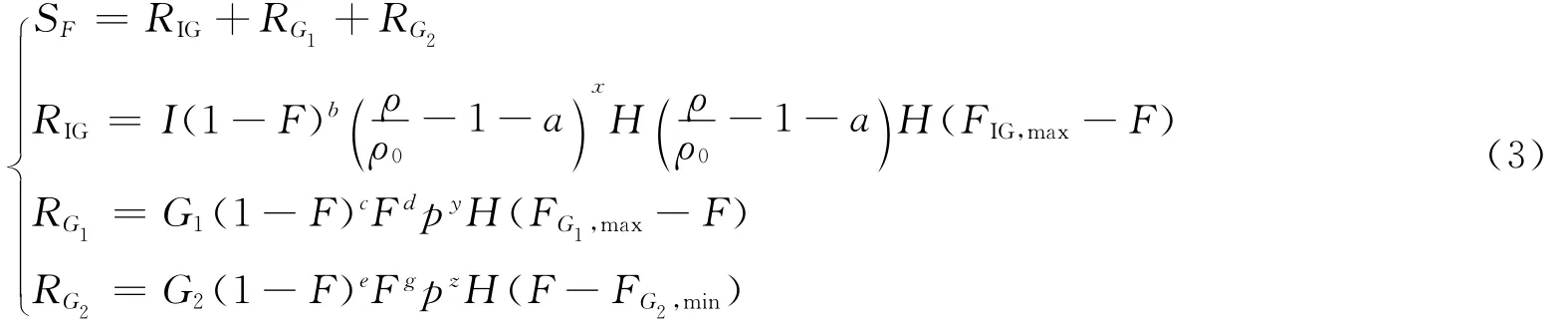
式中：H（x）为阶跃函数，I、G1、G2、a、b、c、d、e、g、x、y、z、FIG，max、FG1，max和FG2，min为炸药参数，ρ0和ρ分别为初始密度和密度，p为压力。RIG、和分别为源项SF的点火项和2个增长项。在炸药冲击点火和爆轰波传播等不同的物理过程中，RIG、和等3项的意义有所差别［5］。

式（2）定义的减敏进程变量ψ通过如下方式进入反应进程变量的控制方程

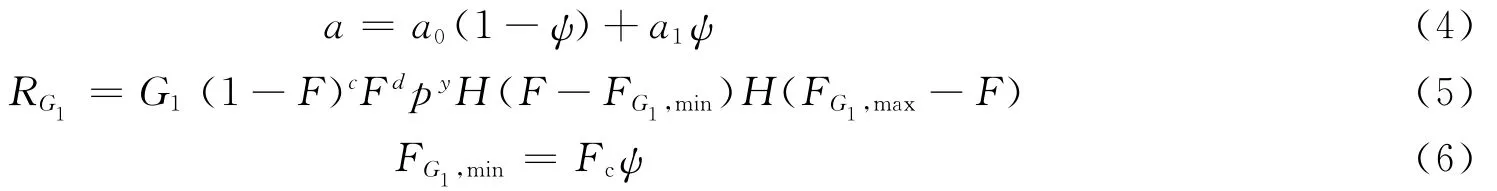
式（4）中的a为式（3）中点火项RIG的压缩率的阈值，a0、a1和Fc为参数。式（2）右端的减敏函数的源项可以采用不同的形式，本文中选取如下表达式［9］

式中：A和ε为参数。则定常压力p下，若减敏进程变量ψ从0积分到ψ1，需时t，积分式（7），可得

1.2 数值计算方法

MEPH2Y采用交替方向方法解无源项的方程组，每个方向为拉氏步计算紧跟输运步计算，当2个方向的无源项方程组解完后计算源项。AMR技术［11］在逻辑上采用嵌套的欧拉型网格块，网格块细分采用在每个方向上一分为二的方式，不同加密级的网格块可选用相等或不等的时间步长，仅计算受到扰动的计算块。在二维爆轰问题计算中，跟踪加密反应区的计算网格。

1.3 状态方程

对炸药反应物、产物均采用JWL状态方程

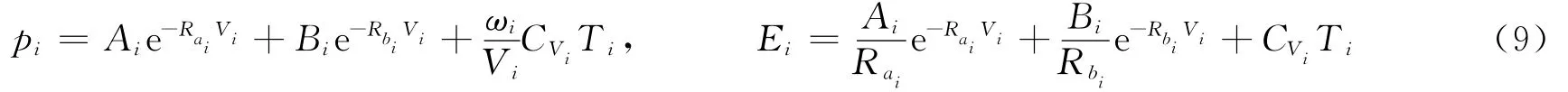
式中：i为s或g，分别代表反应物和产物；Ai、Bi、、、ωi和为参数；V＝ρ0／ρ，E＝ρ0e，e为比内能，T为温度。混合物状态方程采用体积可加、内能可加、温度平衡和压力平衡等假设得到。若定义

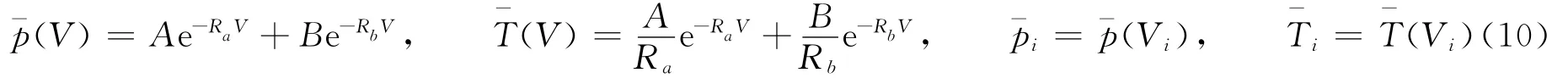
由内能可加、等温假设和状态方程，可得

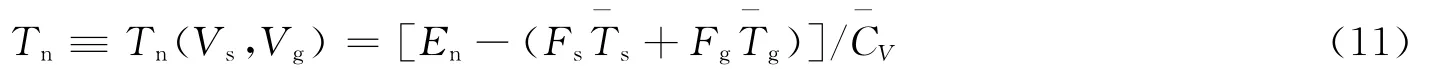
由等压假设、式（11）和状态方程，并考虑到体积可加假设，得到非线性方程

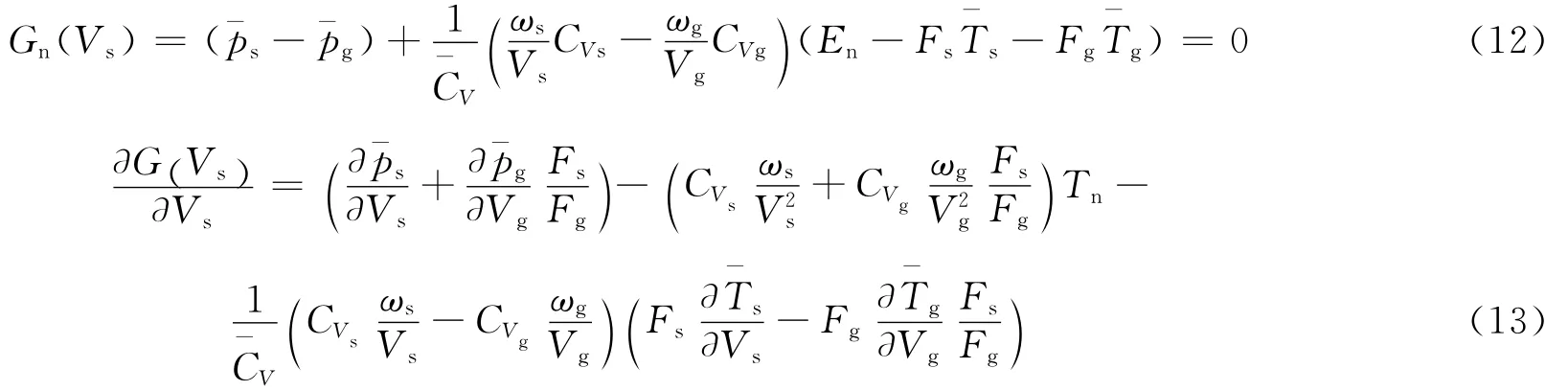
解上述非线性方程，可采用Newton迭代法或二分法。模拟死区时，在稀疏区内对初值的选取要求较严格，Newton迭代往往不收敛到正确解，此时采用二分法较合适。

2 钝感炸药的爆轰数值模拟

2.1 计算参数

算例涉及钝感炸药TATB、LX－17和PBX9502。炸药反应物及产物JWL状态方程和点火增长模型的参数分别采用文献［4，9，5］中相应炸药的参数。炸药LX－17减敏模型的相关参数分别为：A＝8.364 2s－1·kPa－1，ε＝0.001，a0＝0.22，a1＝0.5，Fc＝0.01；其中，A通过将p＝1GPa，ψ1＝0.98，t＝1.29μs代入式（8）得到［9］。

2.2 钝感炸药的冲击点火

以11.38GPa的压力持续冲击TATB，采用1／100mm网格计算。表1为稳定爆轰波爆速、von Neumann尖点和CJ状态，计算值与实验值［4］一致。N和CJ分别表示尖点和CJ状态。

表1 TATB炸药爆轰波的von Neumann尖点和CJ状态参数Table 1Parameters for detonation von Neumann spike and CJ states of TATB explosive

2.3 引入减敏模型的钝感炸药冲击点火

以12.55和14.97GPa的压力持续冲击LX－17炸药，计算中采用1／200mm网格。

图1为不同时刻的压力曲线，从0时刻开始，从左向右依次间隔Δt＝0.1μs，实线为标准模型结果，而虚线为减敏模型结果。采用标准点火增长模型模拟，均能形成自持爆轰；而采用减敏模型模拟，较弱的冲击则不能起爆炸药，这与文献［9］结果一致。

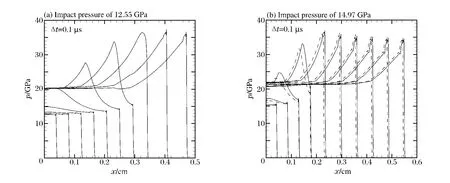
图1 LX－17炸药在不同持续冲击压力下的压力曲线Fig.1Pressure curves of LX－17explosive under different sustaining impact pressures

图2为某时刻不同冲击压力下反应进程变量和阈值的空间分布，引入减敏函数后，在较弱的冲击压力下（见图2（a）），当ρ／ρ0＜1＋a时，反应率中点火项被抑制；F＜时，增长项的发展也被抑制，使炸药无法起爆。而较强的冲击压力下增长项未被抑制（见图2（b）），如图1（b）所示，压力曲线无太大影响，爆轰能够正常形成。

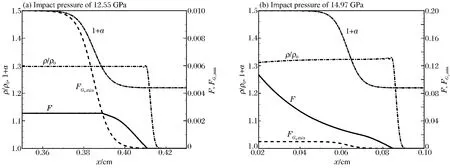
图2 用减敏模型得到的LX－17炸药的压缩率和反应率进程变量的空间分布Fig.2Compression rates and reactive progress variables of LX－17explosive using the desensitizing model

2.4 钝感炸药直径效应

计算中采用轴对称几何，采用AMR技术跟踪反应区，反应区内网格宽度Δx为1／10、1／40mm，初始时刻在柱形 PBX9502炸药的前端设置31.5GPa的高压。图3中给出了药柱内爆轰波传播速度与药柱曲率的关系，实心点线为实验结果［12－13］，空心点线为计算结果。从图中可以看到计算结果有收敛到实验值的趋势。另外，文献［12］中报道在爆速低于7.3km／s时爆轰波将逐渐熄灭。本文中也观察到：较小药柱在较高初始压力（如31.5GPa）下，能够持续较长时间的爆轰波传播；但在较低压力（如14.0GPa）下则会熄灭。

2.5 钝感炸药死区数值模拟

研究带凸井的钝感炸药LX－17，模拟爆轰波在经过拐角后失败，即存在死区的现象。采用文献［9］中模型的几何尺寸，如图4所示，使用柱坐标系。拐角两侧壁面和对称轴为反射边界条件，其他为出口边界条件。初始时刻，在凸井中心R＝7.78mm的半球内，取为爆轰产物（ρ＝ρ0，p＝41.46GPa，F＝1，ψ＝1），之外为反应物（ρ＝ρ0，p＝0，F＝ψ＝0）。采用AMR技术计算，跟踪反应区，反应区内采用1／40mm网格。

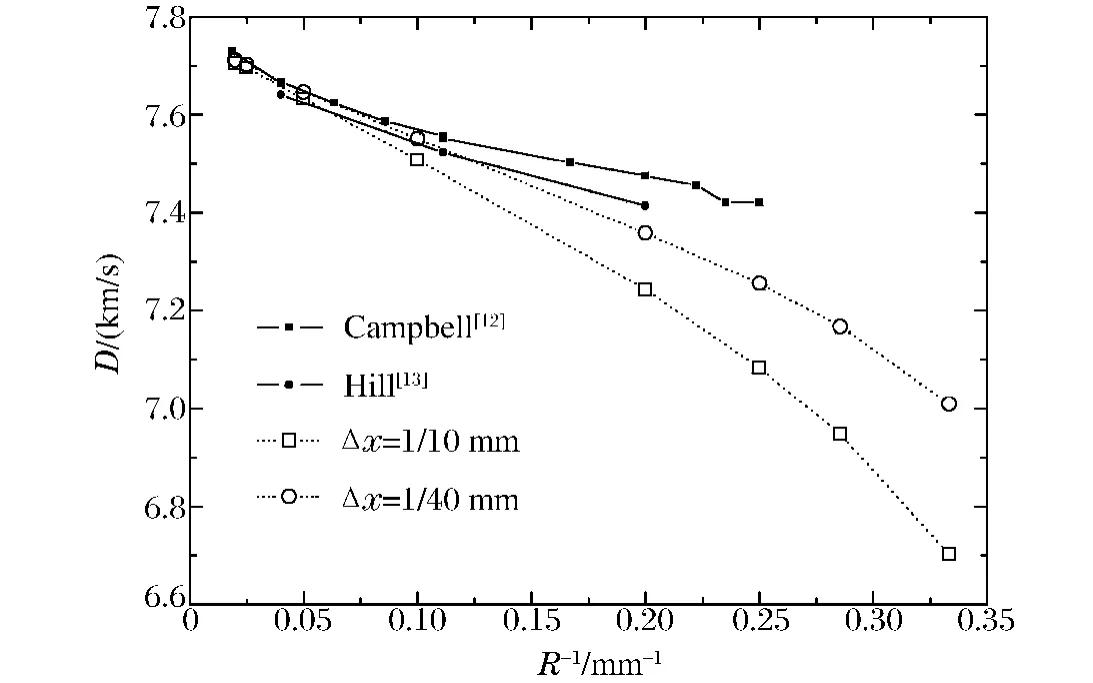
图3 PBX9502炸药的爆速－曲率关系Fig.3Detonation speed－curvature curves of PBX9502explosive

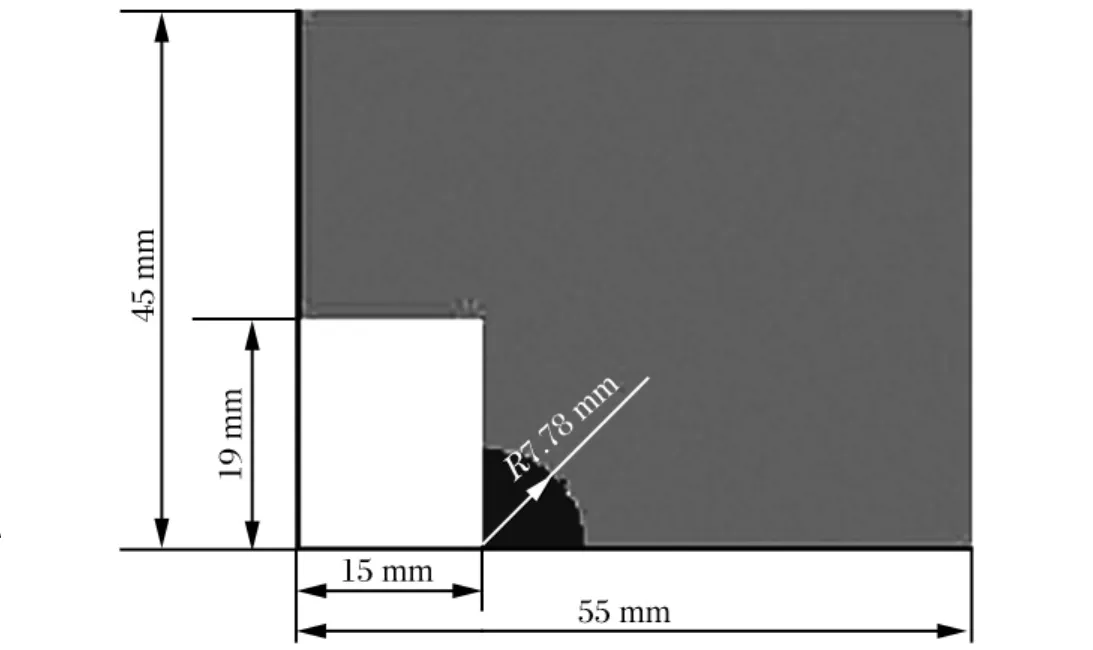
图4 炸药几何形状Fig.4Geometric shape of explosives

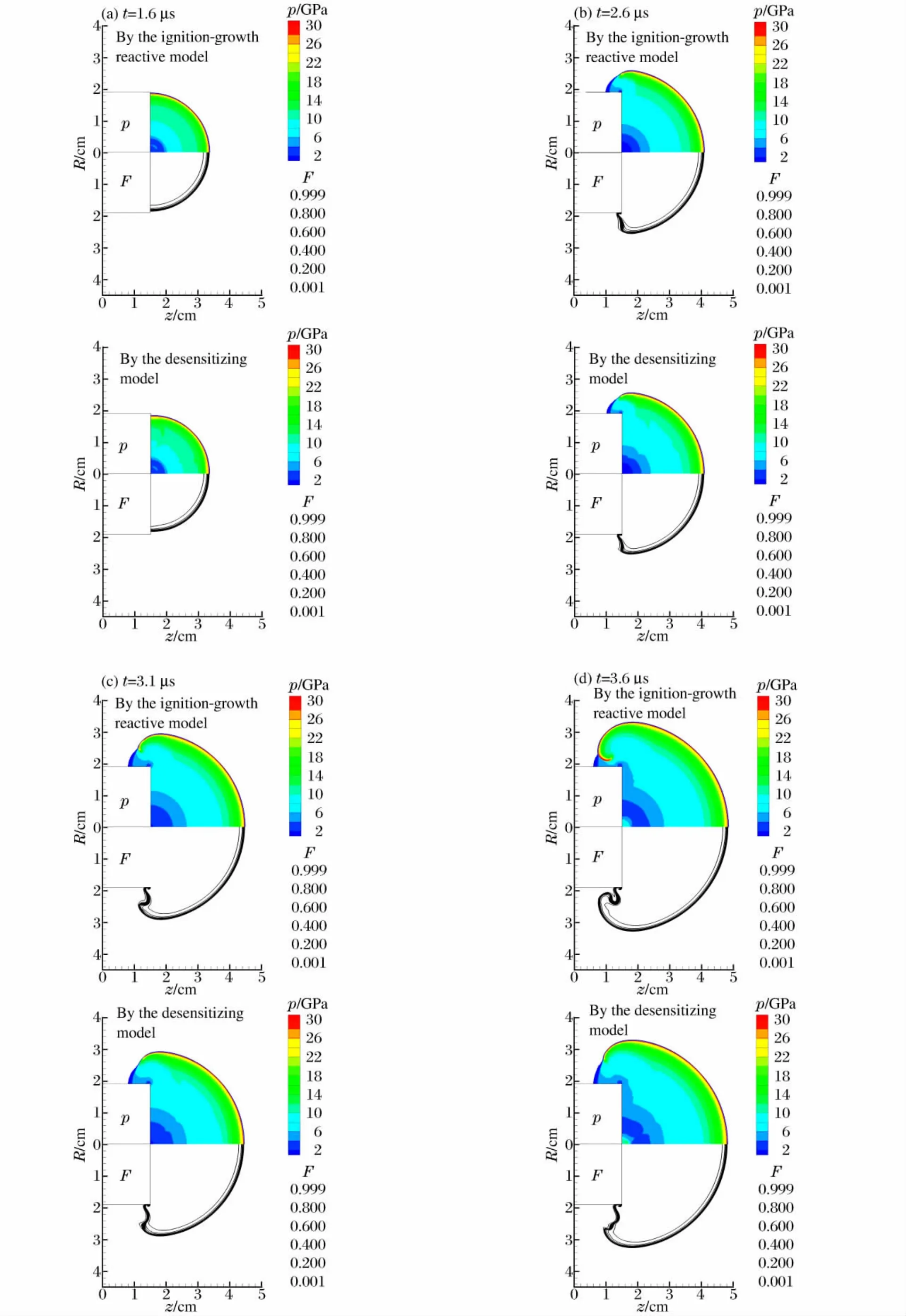
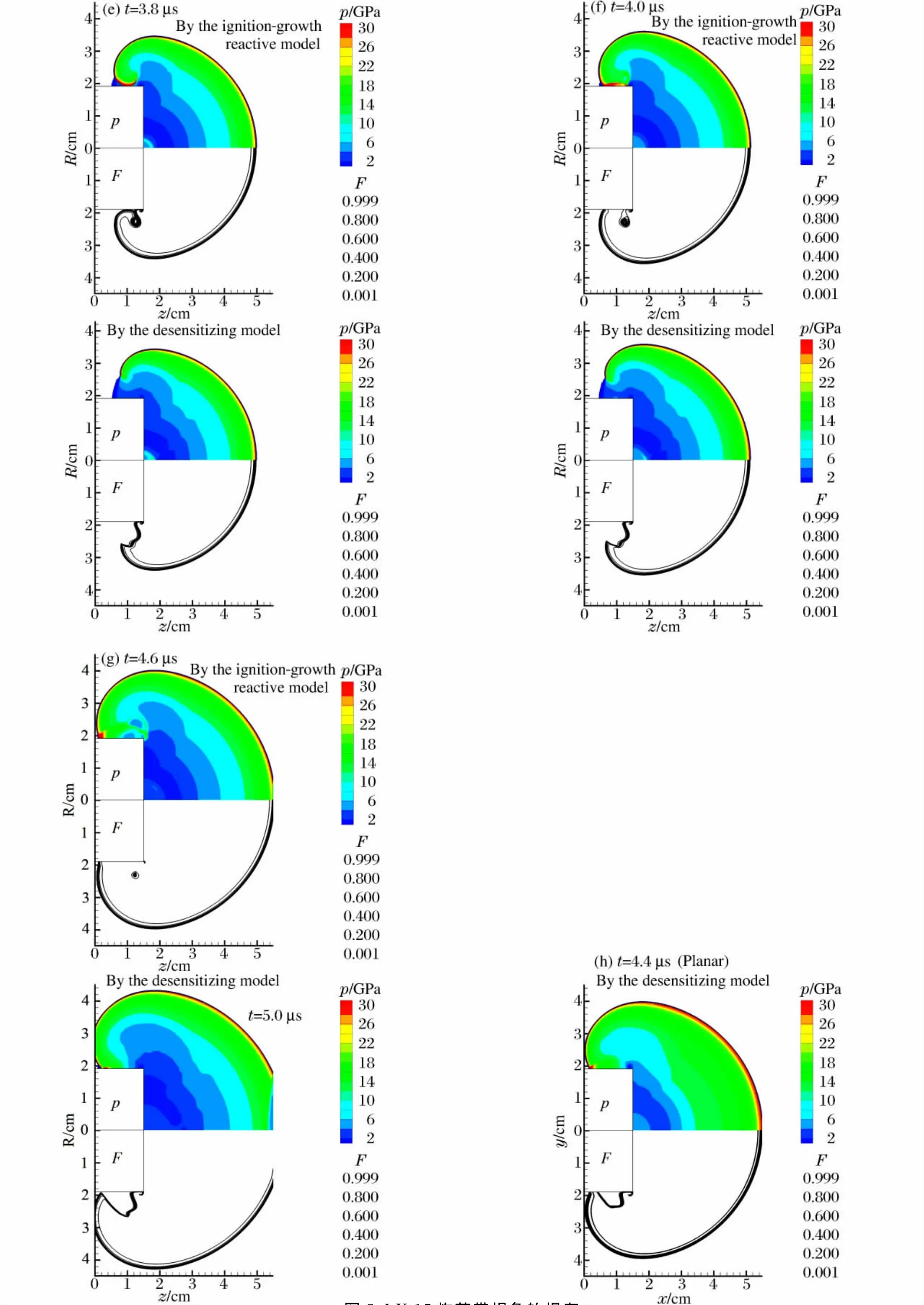
图5 LX－17炸药带拐角的爆轰Fig.5Detonation with the corner of LX－17explosive

图5为数值模拟结果，其中，上排为标准反应率模型计算结果，而下排为带减敏反应率模型的计算结果；每张图的上半部分为压力等值云图，下半部分为反应进程变量等值线。t＜1.6μs（见图5（a）），球面爆轰波逐渐形成并呈球形向外传播，2模型计算结果无明显差别。1.6μs＜t＜2.6μs（见图5（b）），冲击波在拐角处转弯稀疏并开始减弱，压力降低，在拐角附近开始弯曲，在受稀疏的前沿，爆轰波无法形成，而在远离拐角的炸药仍然维持柱面爆轰，2模型结果无明显差别。而后如图5（c）～（f）所示，冲击波前沿严重弯曲，在标准模型中，先前受弱冲击的一部分炸药在二次冲击压力下，点火并形成爆轰，在t＝3.8μs弯曲的冲击波与凸井碰撞，此后如图5（g）中标准模型计算结果所示，大部分炸药被弯曲的冲击波冲击起爆，仅在拐角处有极少量未起爆炸药，即死区仅局部地、暂时地存在；然而，在减敏模型计算中，受弱冲击的炸药敏感性降低，弯曲的较弱的冲击无法使炸药起爆形成爆轰，最终在拐角附近形成死区，直到计算结束，死区仍然存在。值得注意的是，在标准模型计算中，部分受二次冲击的炸药虽然起爆，但该区域的温度始终仅500K左右，对于爆轰来讲不大合理，这也说明减敏模型有一定的合理性，也许反应率函数应该考虑更多的因素。另外，平面几何与轴对称几何的结果相似，标准反应率模型亦仅形成局部、暂时的死区而后所剩无几；而在考虑了减敏效应的模型中死区能够永久存在，如图5（h）所示，只是死区形状略有不同。

3 结 论

在弹塑性流体力学程序中引入点火增长的反应率模型和炸药减敏模型，借助网格自适应加密技术，对钝感炸药的冲击点火、炸药直径效应和带拐角炸药的死区形成等爆轰现象进行了数值模拟。数值结果表明，标准反应率模型能够正确模拟平面爆轰波的特征状态和钝感炸药的直径效应，在引入减敏模型后能够较好地模拟钝感炸药的死区形成过程。钝感炸药的数值研究表明，自主研发的弹塑性流体力学程序应用于炸药研究是可行的。

［1］Fickett W，Davis W C.Detonation：Theory and experiment［M］.Berkeley：University of California Press，1979：13－54.

［2］Johnson J N，Tang P K，Forest C A.Shock wave initiation of heterogeneous reactive solids［J］.Journal of Applied Physics，1985，57（9）：4323－4334.

［3］Starkenberg J.Modeling detonation propagation and failure using explosive initiation models in a conventional hydrocode［C］∥Wardell J F，Maienschein J L.Proceedings of 12th International Detonation Symposium.San Diego，CA：Office of Naval Research，2002：1381－1390.

［4］Lee E L，Tarver C M.Phenomenological model of shock initiation in heterogeneous explosives［J］.Physics of Fluids，1980，23（12）：2362－2372.

［5］Tarver C M，McGuire E M.Reactive flow modeling of the interaction of TATB detonation waves with inert materials［C］∥Wardell J F，Maienschein J L.Proceedings of 12th International Detonation Symposium.San Diego，CA：Office of Naval Research，2002：971－980.

［6］Nichols III A L，Tarver C M.A statistical hot spot reactive flow model for shock initiation and detonation of solid high explosives［C］∥Wardell J F，Maienschein J L.Proceedings of 12th International Detonation Symposium.San Diego，CA：Office of Naval Research，2002：779－788.

［7］Campbell A W，Travis J R.The shock desensitization of PBX－9404and composition B3［C］∥Davis W C.Proceedings of the 8th International Detonation Symposium.Albuquerque，NM：Naval Surface Warfare Center，1985：1057－1068.

［8］Cox M，Campbell A W.Corner－turning in TATB［C］∥Short J M.Proceedings of the 7th International Detonation Symposium.White Oak，MD：Naval Weapons Center，1981：624－633.

［9］DeOliveira G，Kapila A K，Schwendeman D W，et al.Detonation diffraction dead zones and the ignition－and－growth model［C］∥Peiris S M.Proceedings of the 13th International Detonation Symposium.Norfolk，VA：Office of Na－val Research，2006：13－22.

［10］冯其京，何长江，张敏，等.二维高速碰撞问题欧拉数值模拟的混合网格计算［J］.计算物理，2003，20（2）：147－152.

FENG Qi－jing，HE Chang－jiang，ZHANG Min，et al.Calculation of mixed cells in simulating high－speed collision problems with two－dimensional Eulerian hydrodynamic method［J］.Chinese Journal of Computational Physics，2003，20（2）：147－152.

［11］HAO Peng－cheng，FENG Qi－jing，YAO Wen.Two－dimensional Euler adaptive mesh method on detonation［J］.Journal of Beijing Institute of Technology，2009，18（2）：141－145.

［12］Campbell A W.Diameter effect and failure diameter of a TATB－based explosive［J］.Propellants，Explosives，Pyrotechnics，1984，9（6）：183－187.

［13］Hill L G，Bdzil J B，Aslam T D.Front curvature rate stick measurements and detonation shock dynamics calibration for PBX 9502over a wide temperature range［C］∥Davis W C.Proceedings of the 11th International Detonation Symposium.Snowmass，CO：Office of Naval Research，1998：1029－1037.