弹体侵彻过程中装药温升的近似分析＊

孙宝平，段卓平，皮爱国，欧卓成，黄风雷

（北京理工大学爆炸科学与技术国家重点实验室，北京 100081）

弹体对目标侵彻过程中，战斗部装药会在惯性作用下受到持续时间为几毫秒的载荷作用，这可能会导致装药破裂或早爆。因此，弹体内部装药的安全性是目前迫切需要解决的问题。弹体在侵彻混凝土类介质的过程中承受的过载大大高于空气中飞行时的过载，一般在（2×103～3×104）g（g为重力加速度）之间［1］。在接触靶板和侵彻过程中，靶板介质阻碍弹体侵入，弹体速度减小。由于弹体内部装药自身的惯性作用（受到惯性冲击载荷）将产生轴向压缩和径向应力，当弹体内壁与装药发生相对运动时，摩擦功作为热源引起装药的温升。李德聪等［2］基于炸药热爆炸理论，采用炸药热点温度作为侵彻过程中内部装药起爆判据，得出炸药装药和弹壳接触面间的摩擦是形成热点和装药起爆的原因。赵生伟等［3］在130mm轻气炮上进行了模拟装药实验，并进行了数值模拟，将实验结果和数值模拟得到的压力p和应力波等效脉宽τ以p2τ≤常数作为判据初步评价了装药的安全性。虽然p－τ判据可对侵彻过程中内部装药能否发生爆炸做出判断，但并不能对装药局部点火、燃烧等弱反应进行判定，这些弱反应在某些条件下也可能转化成强反应，如燃烧转爆轰等，这将严重影响弹体装药的安全性。

本文中主要考察弹体侵彻过程中弹体内壁与装药摩擦使局部装药所能达到的最高温度，并以该类药剂的点火温度作为装药安全性的临界值，此判据比p－τ判据能够更早地揭示装药中存在的安全隐患，这为弹体侵彻过程中的装药设计和安全性分析提供理论依据。

1 物理模型与力学分析

一般情况下，弹体头部为圆锥体或类圆锥体，主体部分为圆柱体，内部装药与弹体外形相似。为了便于描述和计算，假设弹体正侵彻靶板，弹体内装药为圆柱体，弹体受到阻力F，与弹体运动速度方向相反，弹体的过载为a，如图1所示。假设装药为各向同性体，采用弹塑性线性硬化模型描述，如图2所示。装药受到弹体内壁的约束，由于弹体的弹性模量远远大于炸药的弹性模量，二者之比为约50，因此，可以忽略装药的环向应变εθ和径向应变εr，装药处于三向压应力状态（单轴应变），此时

设装药长度为H，装药直径为D，装药密度为ρ，任一位置处的轴向应力、径向应力和环向应力分别为σz、σr和σθ。对于圆柱形装药，沿轴向的各截面上产生的应力大小不等，而每个截面上的应力处处相等。在此作近似推导，距离头部z处的轴向应力表达式为

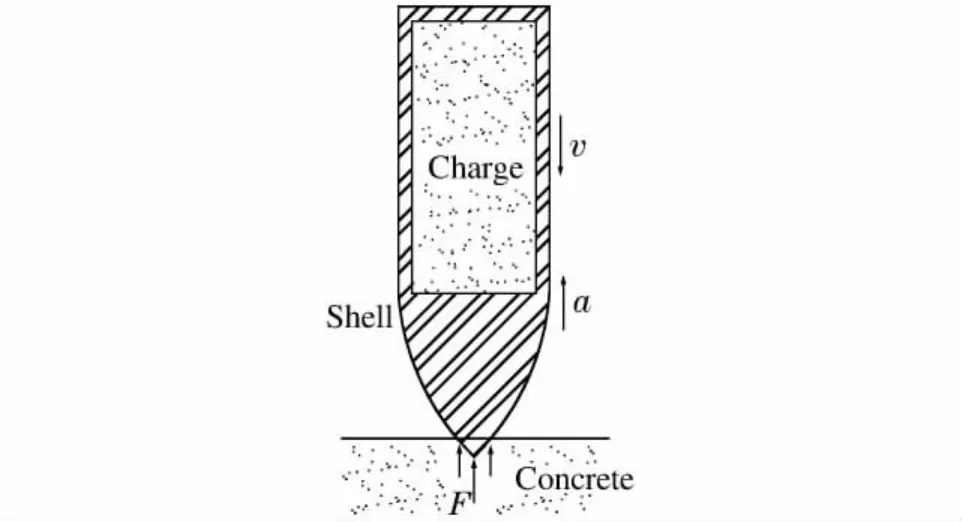
图1 弹体与简化的内部装药示意图Fig.1Schematic diagram of projectile and simplified charge

图2 装药弹塑性线性强化模型Fig.2Elastic－plastic linear hardening model of charge

由于装药各个截面的轴向应力并不相同，头部最大，尾部最小，装药变形过程中将会有塑性变形和弹性变形2个部分，图3给出了弹性区和塑性区的示意图。

当z＞zp时，炸药处于弹性状态，根据广义弹性虎克定律，σθ＝σr，与轴向应力σz有下列关系

式中：ν为炸药泊松比，ν取值在0～0.5之间，σθ和σr均小于σz。将式（3）代入式（5），得到轴向应变为

图3 装药弹性和塑性变形分区示意图Fig.3Schematic diagram of zones of elasticity and plasticity

采用Tresca屈服准则或者Von－Mises屈服准则，得到相同的装药屈服函数为

式中：σy为装药屈服应力。

将式（3）代入式（7）中，得到弹性区和塑性区的分界线为

当z≤zp时，装药处于塑性状态。炸药采用弹塑性线性硬化模型，轴向应力σz由式（3）来描述，轴向应变εz为

式中：E为弹性模量；Et为切线模量。

装药塑性部分的形变量u为

弹性部分的形变量u分为2个部分，一是塑性部分累积的形变量，另一部分是弹塑性分界线至弹性部分某位置的形变量

2 理论计算

2.1 传热时间与传热特征尺寸的估算

单轴应变状态下，弹性波在介质中传播速度c为

弹性波在装药达到应力平衡前的传播时间t为

式中：α为热扩散率，α＝κ／（ρcp）；κ为导热率；cp为比热容。

装药以PBX9404炸药为例，炸药的物性参数［6－7］：炸药密度ρ2＝1.84g／cm3，炸药弹性模量E＝5GPa，κ2＝432mW／（m·K），cp2＝1 130J／（kg·K），Et＝600MPa，σy＝40MPa，ν＝0.224。弹体的物性参数［8］：壳体密度ρ1＝7.8g／cm3，κ1＝46.4W／（m·K），cp1＝500J／（kg·K）。

当H＝1.5m时，由式（13）计算出t＝1.5ms，由式（14）计算出弹体内壁热传导的特征尺寸为L＝130μm，炸药热传导的特征尺寸L＝17μm，弹体内壁与装药之间摩擦生成的热量不会传至圆柱中心轴，也不会传至弹体的外表面，因此，弹体内壁和炸药摩擦生成的热量不会与体系外的环境发生热交换。

2.2 装药的温升

装药与内壁的摩擦系数为μ，摩擦速率v、比摩擦力σf和比摩擦功率q分别为

式中：γ为常数，由于弹体内壁与装药摩擦作用时间取决于波在装药中的传播时间，一般为波在装药中的一次往返时间，γ取值为2。

在一定时间内，热能够传输的距离被称为热扩散距离，扩散距离L的特征尺寸［4－5］为

传入弹体内壁和炸药中的比摩擦功率分别为q1和q2，可推导出

弹体内壁和炸药摩擦生热与外部环境不发生热交换，根据热平衡方程，最高温升［9－10］

式中：ierfc（x）为余误差函数erfc（x）的积分。

由式（3）、（11）、（15）～（18）可得到弹性区温升为

由式（3）、（10）、（15）～（18）可得到塑性区温升为

2.3 装药中最高温升的位置

当弹体内壁和装药物性参数、装药长度确定的情况下，式（20）和（21）对z求导，可以求出最高温度在装药中的位置，此处也是装药最容易发生点火的位置。在弹性区（zp，H］，温升ΔT单调递减，当z＝zp时，ΔT最大。在塑性区［0，zp］，温升最大的位置为zT，max，也是整个装药中温升最高的位置，zT，max为

对式（22）进行量纲一化，取装药长度H为度量基本单位，得到

图4 不同过载时温升最高处在装药中的相对位置与装药长度的关系Fig.4Relative position of the highest temperature varied with the charge length at different overloads

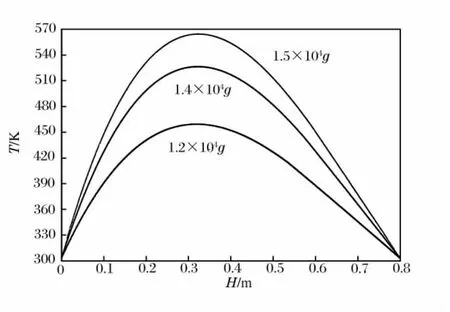
图5 装药在不同最大过载时的温度分布曲线Fig.5Temperature distribution in the charge explosive at different peak overloads

弹体内壁与装药摩擦发生点火的相对位置与装药长度H、炸药物性常量M、过载最大值a有关。对于PBX9404装药，当M＝2.61×103m2／s2时，最大过载分别为1.5×104g、1.0×104g和1.2×104g条件下温升最高处在装药中的相对位置如图4所示。随着装药长度的增加，最高温升出现在装药中的相对位置趋近于0.40～0.42之间，装药长度H在0.8m以上，这个位置也是装药最先发生点火的位置。

PBX9404炸药的点火温度为506.5～514.5K［11］，设装药与弹体内壁的摩擦因数μ为0.03。图5给出了装药长度为0.8m，过载分别为1.5×104g、1.4×104g和1.2×104g时装药的温度分布。最大过载为1.5×104g时，装药的最高温度为564K（初始温度为303K），出现在炸药0.322m 的位置，相对位置为0.403；最大过载为1.4×104g时，装药最高温度为526K，出现在炸药0.324m的位置，相对位置为0.402；最大过载为1.2×104g时，装药最高温度为459K，出现在炸药0.319m的位置，相对位置为0.398。可以看出，随着最大过载的增大，体系所能达到的最高温度有所提高。由于弹体侵彻混凝土靶板的最大过载值一般在1.5×104g以下［1］，因此，当最大过载值为1.5×104g时，装药内的最高温度超过了PBX9404炸药的点火温度。

图6给出最大过载为1.5×104g条件下装药长度分别为0.6、0.7、0.75和0.8m 时的温度分布曲线。装药长0.8m时，最大温度为564K；装药长0.75m时，最大温度为522K；装药长0.7m时，最大温度为483K；装药长0.6m时，最大温度为419K。从图6中可以看出，随着装药长度的提高，体系所能达到的最高温度值也越来越大，超过了炸药的点火温度，更容易发生点火反应。当装药长为0.75m时，装药内部所能达到的温度与该炸药的点火温度相近，故0.75m为装药的临界长度。因此，最大过载为1.5×104g时，装药长度小于0.75m是比较安全的。根据上述分析，弹丸设计中如果装药长度大于临界长度，则可以考虑分段装药，每段装药长度均要小于临界装药长度，装药之间采用吸热性能较好的材料作为隔垫，以解决摩擦引起的炸药点火问题。

图6 1.5×104 g过载时不同装药长度的温度分布曲线Fig.6Temperature distribution in the charge explosive with the different lengths at the peak overload of 1.5×104 g

3 结 论

（1）弹体侵彻过程中高过载引起的装药点火是影响装药使用安全性的重要因素，点火温度作为装药安全性的判据，以摩擦产生的温升判断装药的安全性具有一定的客观性。

（2）装药最高温升以及最高温升在装药中的位置与其物性参数、装药长度和侵彻过载最大值相关。

（3）通过最高温升计算式可以确定装药使用时的安全临界长度，可用于侵彻弹的装药长度设计。

本文中仅考虑了弹体内壁与装药摩擦引起的点火反应，尚未考虑非对称载荷、剪切、裂纹等机制引发的炸药点火问题，下一步将对此展开研究。

［1］周宁，任辉启，沈兆武，等.侵彻钢筋混凝土过程中弹丸过载特性的实验研究［J］.实验力学，2006，21（5）：572－578.

ZHOU Ning，REN Hui－qi，SHEN Zhao－wu，et al.Experimental study on overload characteristics of projectile penetrating reinforced concrete［J］.Journal of Experimental Mechanics，2006，21（5）：572－578.

［2］李德聪，陈力，丁雁生.装药弹体侵彻混凝土厚靶中的炸药摩擦起爆模型［J］.爆炸与冲击，2009，29（1）：13－17.

LI De－cong，CHEN Li，DING Yan－sheng.A model of explosion induced by friction in the process of loaded projectiles penetrating in to concrete targets［J］.Explosion and Shock Waves，2009，29（1）：13－17.

［3］赵生伟，初哲，李明.抗侵彻过载战斗部装药安定性实验研究［J］.兵工学报，2010，31（增刊1）：284－287.

ZHAO Sheng－wei，CHU Zhe，LI Ming.Experiment investigation on stability of explosive in anti－overload warhead［J］.Acta Armamentarii，2010，31（Suppl 1）：284－287.

［4］Meyers M A.Dynamic behavior of materials［M］.New York，USA：John Wiley ＆Sons，Inc，1994.

［5］Amosov A P，Bostandzhiyan S A，Kozlov V S，et al.Mechanism of heating up and ignition of solid explosives due to external friction as a result of mechanical stimulations［J］.Combustion，Explosion，and Shock Waves，1976，12（5）：627－631.

［6］Gibbs T R，Popolato A.LASL explosive property data［M］.Berkeley，USA：University of California Press，1980.

［7］Dobratz B M，Crawford P C.LLNL explosive handbook：Properties of chemical explosive stimulants［M］.Berkeley，USA：University of California Press，1985.

［8］《机械设计手册》上册（第一分册）［M］.第2版.北京：化学工业出版社，1987.

［9］Dienes J K.Frictional hot－spots and propellant sensitivity［C］∥Materials Research Society Symposium Proceedings.New York，USA：Elsevier Science Publishing Co.Inc.，1984：373－381.

［10］雷柯夫A B.热传导理论［M］.裘烈钧，丁履德，译.北京：高等教育出版社，1955.

［11］张杏芬.国外火炸药原材料性能手册［M］.北京：兵器工业出版社，1991.