滚动摩擦隔震结构实时拟动力试验数值积分方法

王静，龚志方，马俊涛，张振凯，葛楠

(河北联合大学，河北省地震工程研究中心，河北唐山 063009)

0 引言

在动力反应数值分析方法中，隐式格式能使计算过程中产生的误差逐渐减小，不会累积到恶化的程度，因而无条件稳定格式都是隐式的，而显式格式不具备这一功能。因此在结构动力分析中一般都采用隐式方法［1］。

结构拟动力试验中更重视隐式方法的应用［2-9］，这是因为在试验过程中，除了数值计算过程中产生误差以外，还有量测传感器本身精度误差、读数误差等，使稳定条件更不容易得到满足。虽然隐式方法对于结构动力分析的数值计算是没有困难，但在拟动力试验当中隐式数值积分方法是无法应用的，因为隐式方法在下一步加载位移的同时要用到下一步的恢复力，而恢复力也是下一步加载位移后需要测量的，所以拟动力试验方法中下一步的加载位移必须是已知的或称为显式的。虽然现在在传统的拟动力试验中可以采用隐式数值积分方法进行拟动力试验［1］，但在实时拟动力试验中，由于联机迭代需要较长的时间，实际上也是无法应用的，因此需要采用子结构技术，将整个结构分成试验子结构与计算子结构两部分，在试验子结构中采用传统的显式数值积分方法，而在计算子结构部分采用无条件稳定的隐式数值积分方法，形成组合数值积分方法［1］。

另一方面，结构拟动力试验涉及到设计到速度相关装置，其恢复力与位移及速度往往表现为复杂非线性的关系(例如FPS摩擦摆隔震支座或RFPS摩擦摆辊轴隔震支座)，在大位移运动条件下其控制方程是非线性常微分方程，难以由隐式格式推导出显式的计算公式，因此对隔震支座部分的运动方程，也应该直接采用隐式格式的计算公式，因此在整体结构中将出现三种子结构:隔震子结构、试验子结构及计算子结构。本文以一个7层采用ERFPS偏心辊轴摩擦摆隔震支座的结构为例，推导了考虑这三种子结构时地震动力反应计算组合数值积分方法－改进子结构法，并给出了在实时拟动力试验中具体应用过程。

1 改进子结构法计算公式

设置滚动摩擦装置的结构如图1所示。设偏心辊轴截面转角为q，则可作为反应隔震装置的广义坐标，q的运动方程具有如下的形式［10］:

其余质点m1至mn的运动方程与一般多自由度系统的运动方程相同，具有如下的形式:

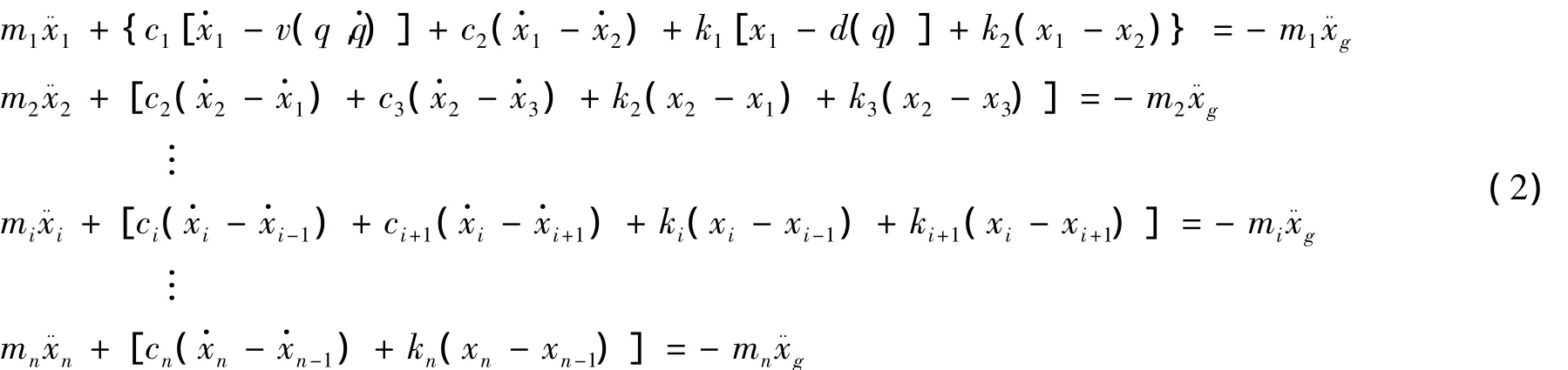
式中，θ是滑块偏离滑道中心的角度;r是滑道半径;ci、ki分别是第i层的阻尼系数及刚度系数;xi，及x¨i分别是质点mi的运动位移、速度及加速度;μs是滑动摩擦系数;g是重力加速度;是地震地面运动加速度;d与v分别是隔震支座的运动位移及速度。

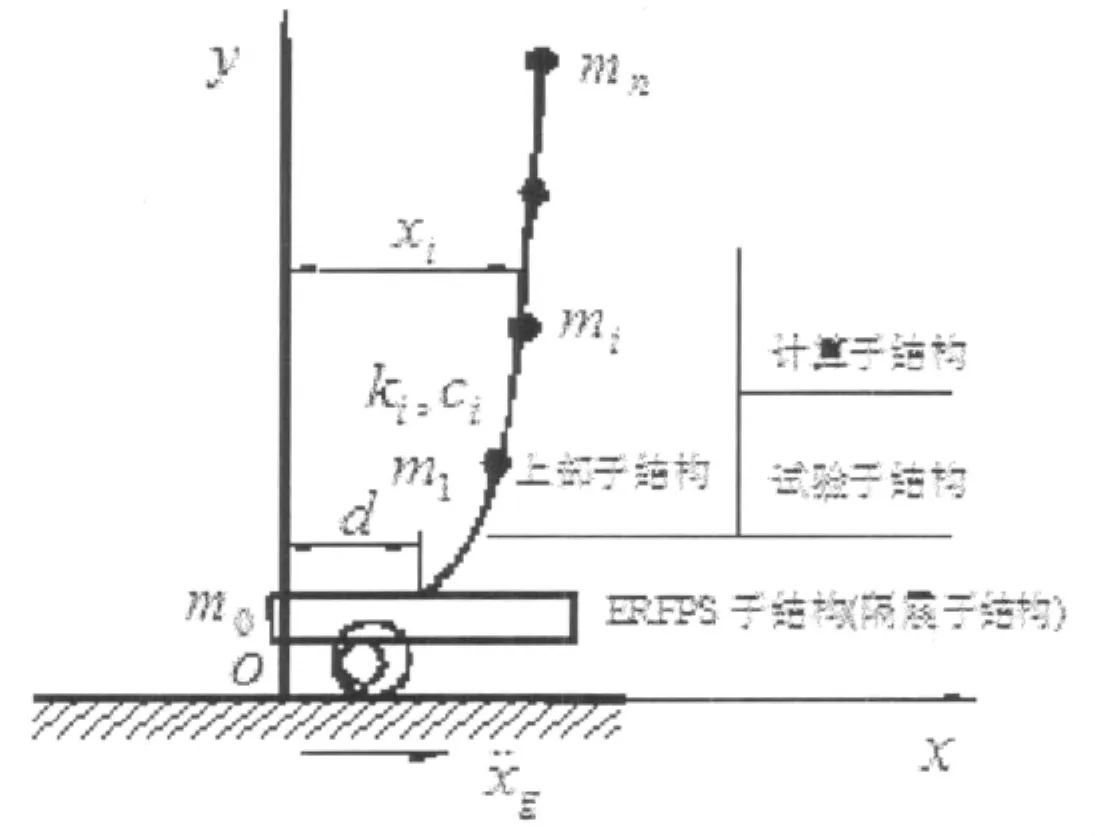
图1 结构分析模型

从式(1)及(2)中的第一式中可以看出，q与x1，x2，x3….构成复杂的非线性耦合关系，若采用隐式动力时程分析法，得出组合求解计算公式是不可能的。因此必须考虑完全显式的方法。但在(1)式及(2)式中，只有自由度q具有非线性的表示关系，x1，x2，x3….表现为线性的，因此可以对q采用显式的格式而对x1，x2，x3….采用隐式格式，即将整体结构分解成了ERFPS子结构(非线性子结构)及上部子结构(线性子结构)。各个自由度的位移与速度按如下的公式计算:

对于自由度q，采用常加速度公式，有:

对于自由度 x1，x2，x3….，采用 Newmark －β 法(隐式)公式，有:

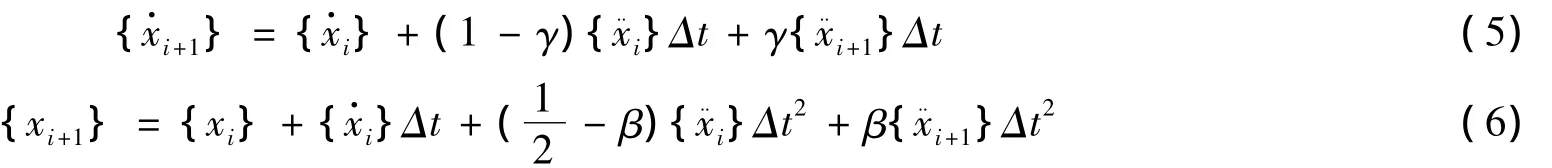
将(3)式代入到(2)式，并将(2)式中的第一个方程化成如下的形式:

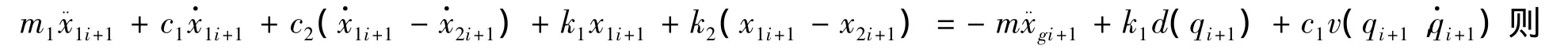
(2)式可化成以下的形式:

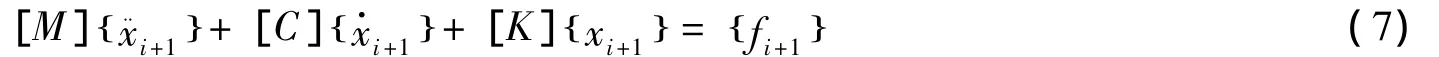
其中:

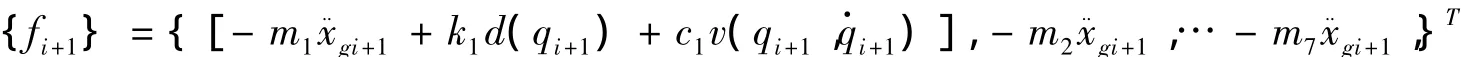
将(5)式、(6)式与(7)联立求解，得出{xi+1}后，将代入到(1)式的离散形式中求出，即完成一个循环。计算过程如图2所示。

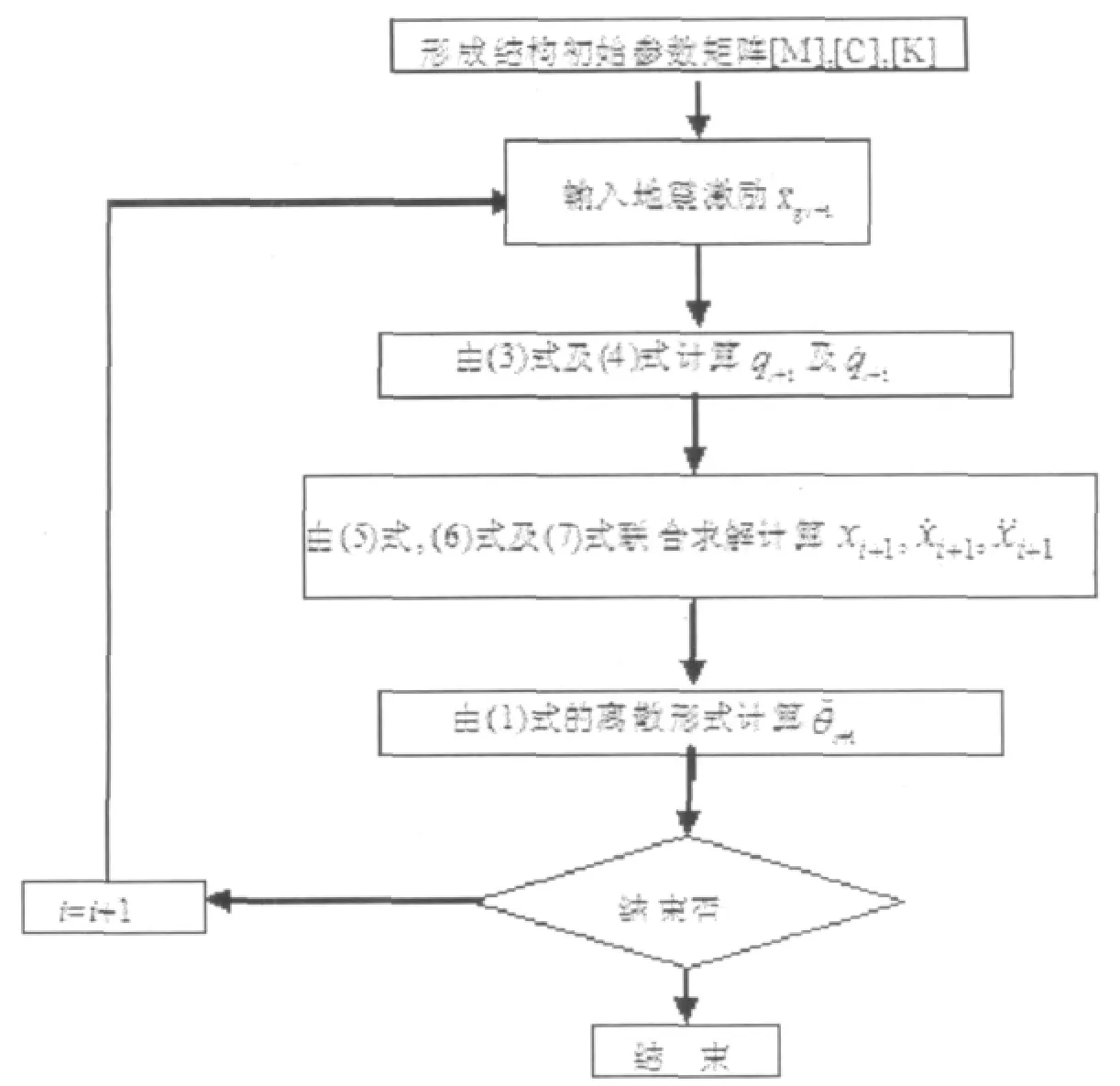
图2 改进子结构计算方法流程图

根据改性子结构计算出动力反应时程，计算结果如图3至图5所示。

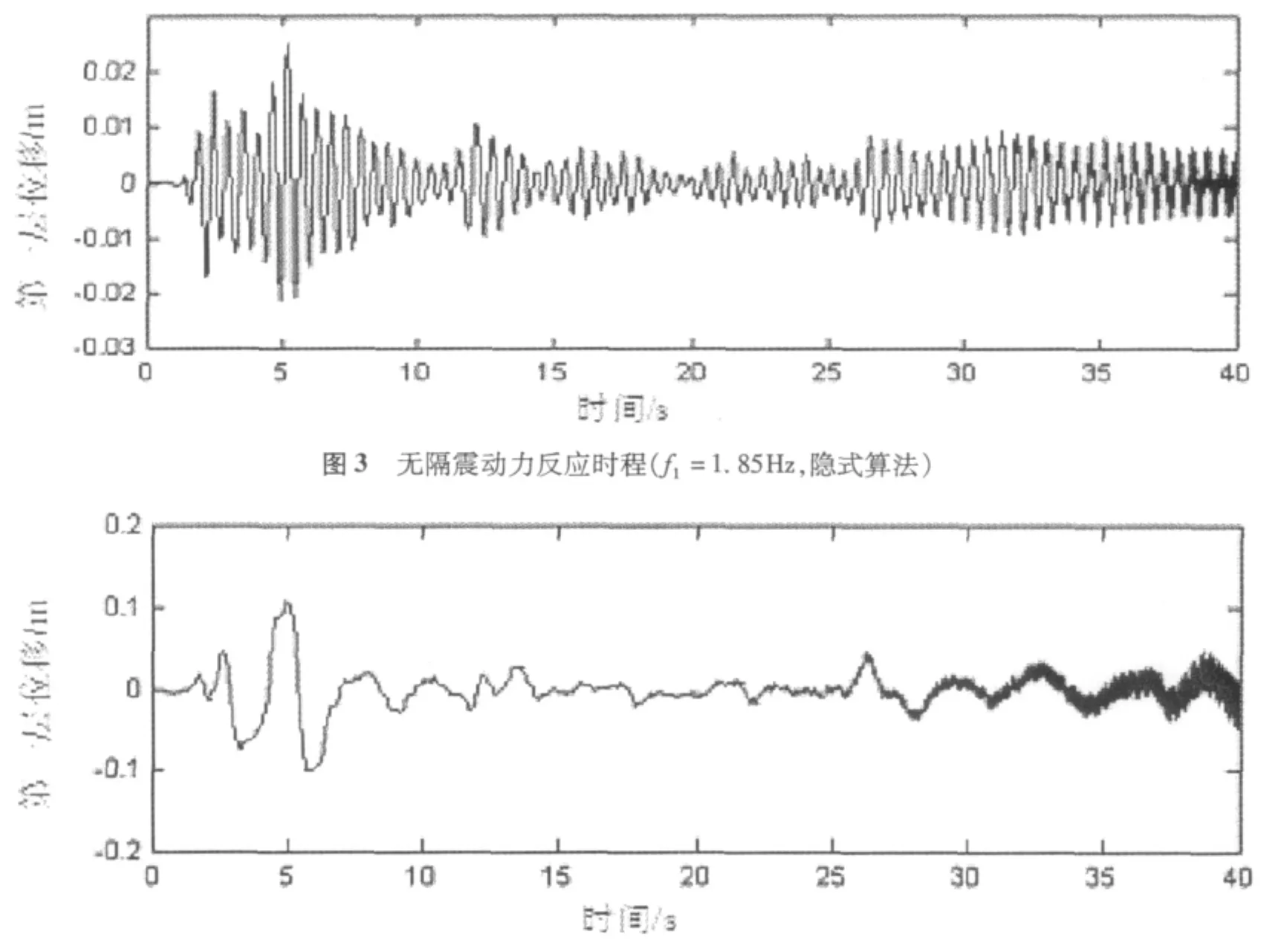
图4 FPS隔震动力反应时程(f1=0.86Hz，显式算法)

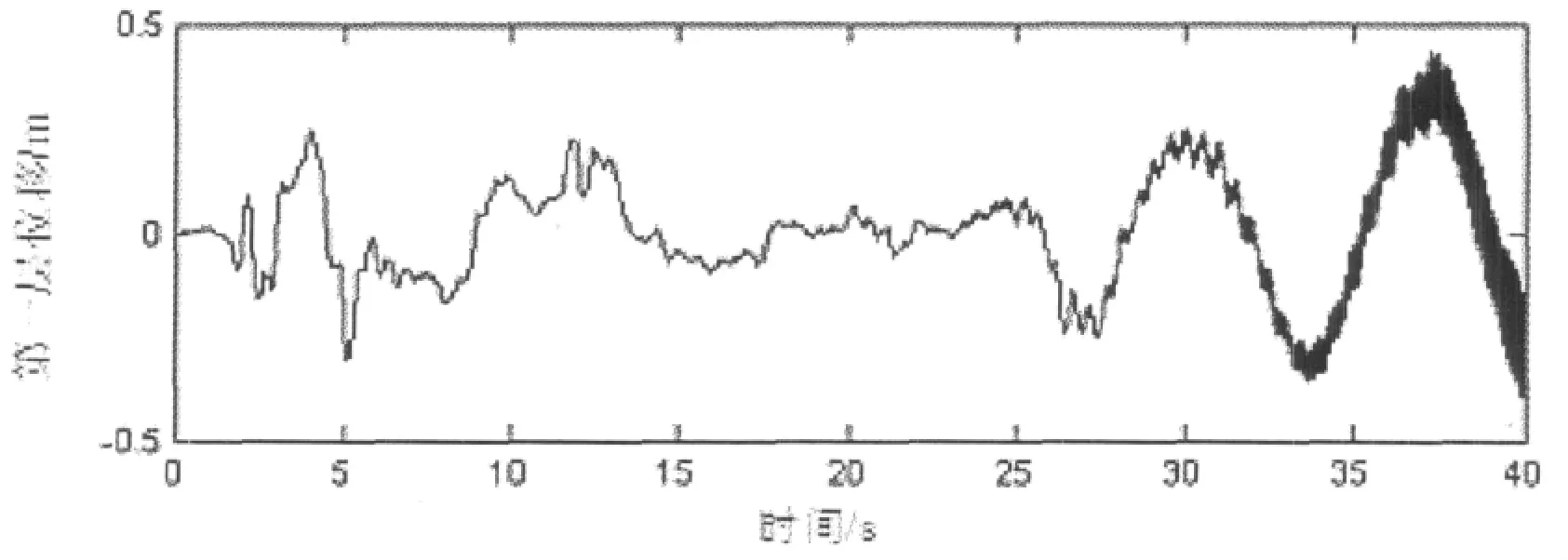
图5 FPS隔震动力反应时程(f1=1.10Hz，改进子结构算法)

有图3至图5可以看出，采用了改进的Newmark-β之后，结构计算稳定的上限频率由0.85Hz提高到了1.11Hz，稳定性要求有所放松。

2 改进子结构法在实时拟动力试验中的应用

虽然在上一节实现了RFPS子结构与上部子结构的组合数值积分方法，但是在拟动力试验当中，是无法直接应用的，因为k1［x1i+1－d(qi+1)］是第i+1步时传感器的反力ri+1，应该在施加完di+1之后由传感器测量读数获得，但是在计算d(qi+1)的过程中也需要用到ri+1=k1［x1i+1－d(qi+1)］。因此，根据PC-Newmark方法，将上部子结构再划分为试验子结构(m1)与计算子结构(m2～m7)，则(7)变成如下的形式:

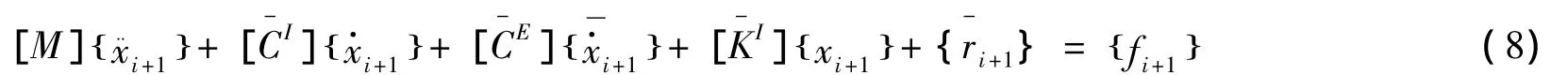
其中:

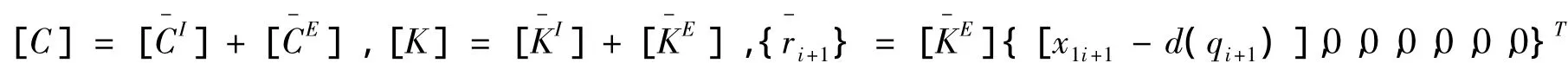
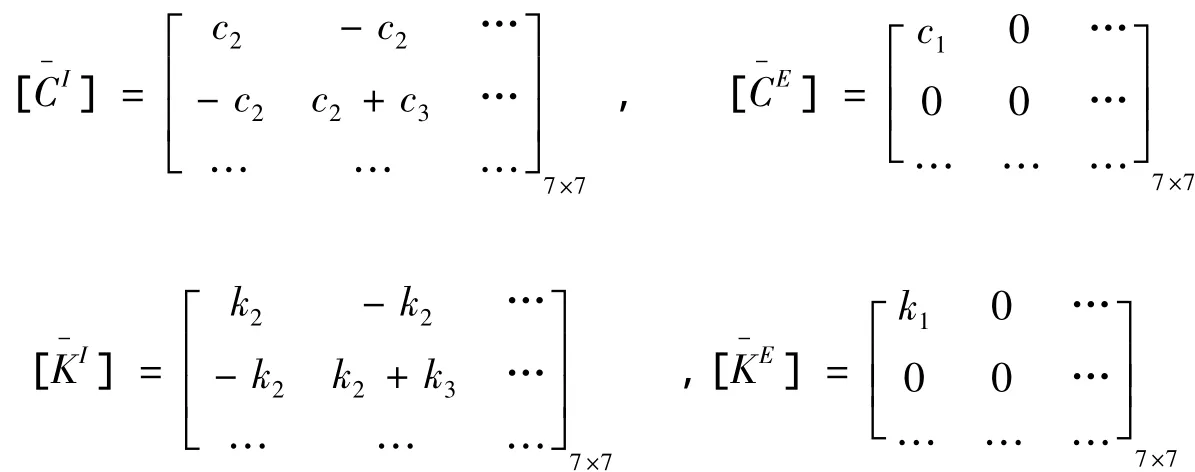
根据PC－Newmark法计算公式，有:

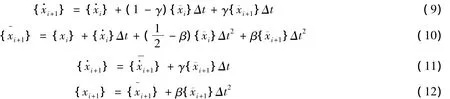
再由qi+1和根据(1)的离散形式求出，完成一个循环。

因为式(9)及式(10)用于预测位移与速度，而式(11)及式(12)用于校正位移与速度，是在每一个时间离散点的最后数值。预测位移是拟动力试验中试件要达到的位移，而校正位移只用于下一步位移的计算。预测－校正Newmark法的试验流程见图6，在编制程序时也是非常容易实现的。

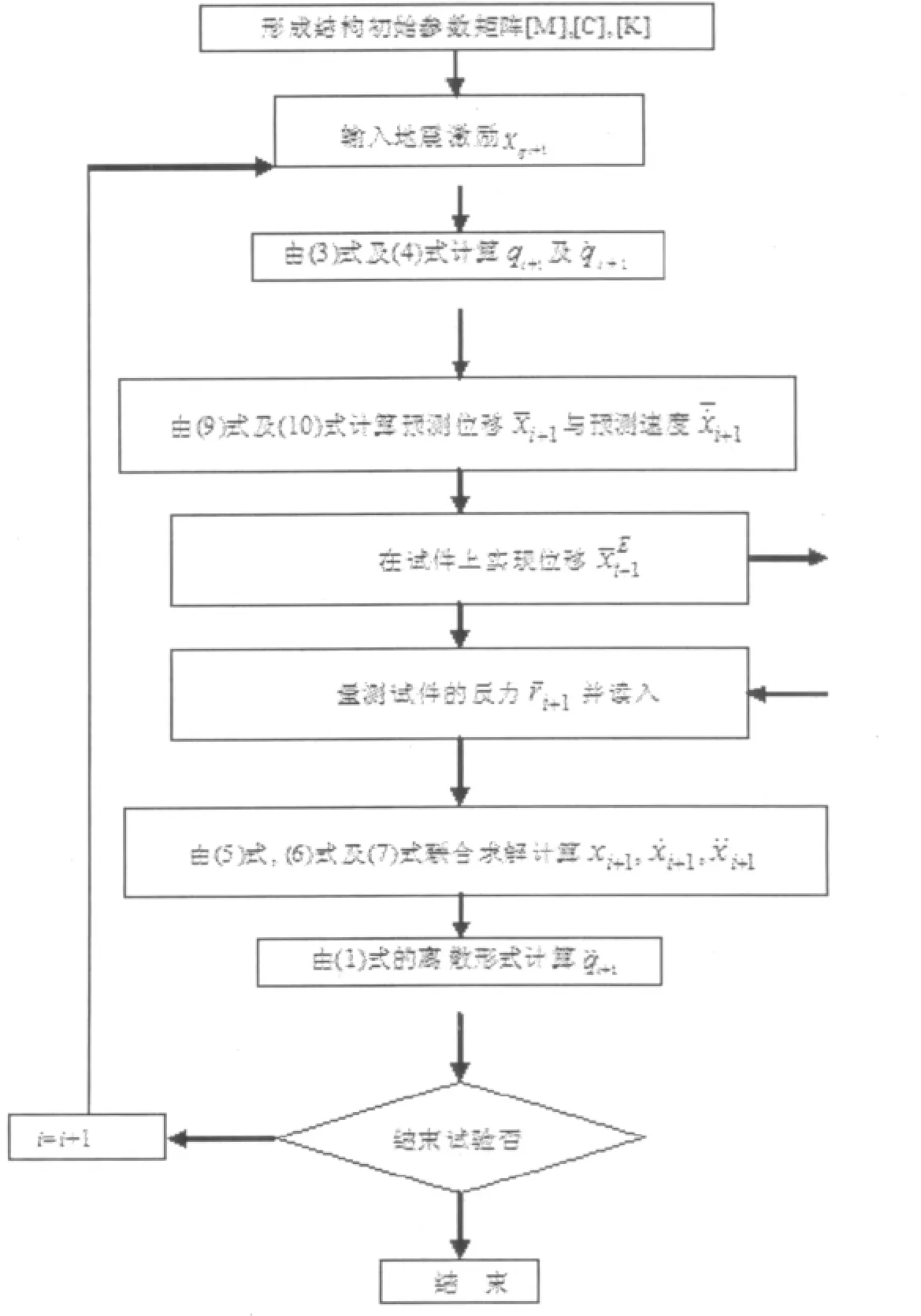
图6 改进子结构计算方法流程图

3 结论

将有设有滚动隔震装置的结构实时拟动力试验模型分开成隔震子结构、试验子结构及计算子结构的做法是可行的，对隔震子结构、试验子结构分别采用显式算法，解决了隔震子结构运动方程的非线性及实验子结构中作动器反力的量测及输入问题。对计算子结构采用隐式算法公式，可以在一定程度上放松数值计算稳定性条件的限制。

［1］邱法维.联机结构试验中的子结构技术及其应用［J］.实验力学，1995，10(4):335-342.

［2］肖岩，胡庆，郭玉荣，等.结构拟动力远程系统试验网络平台的开发研究［J］.建筑结构学报.2005，26(3):122-129.

［3］吕建民，郭玉荣，肖岩.结构远程协同试验研究进展［J］.建筑科学与工程学报.2006，23(4):38-43.

［4］田石柱，蔡新江.远程协同结构试验方法研究与发展［J］.地震工程与工程振动.2006，26(5):47-54.

［5］郭玉荣，张国伟，肖岩，等.单自由度结构远程分析及拟动力实验平台［J］.湖南大学学报.2006，33(2):18-21.

［6］M.Nakashima.Part II:Relationship Between Integration Time Interval and Response Stability in Pseudodynamic Testing［J］.Journal of Structural Construction Engineering.AIJ，1985，(358):35-40.

［7］S.Y.Chang.Explicit pseudodynamic algorithm with unconditional stability［J］.Journal of Engineering Mechanics.2002，128(9):935-947.

［8］R.Peek，W.H.Yi.Error Analysis for Pseudodynamic Test Method I:Analysis［J］.Journal of Engineering Mechanics.1990，116(7):1618-1637.

［9］R.Peek，W.H.Yi.Error Analysis for Pseudodynamic Test Method II:Application［J］.Journal of Engineering Mechanics，1990，116(7):1638-1658.

［10］葛楠，苏幼坡，王兴国，等.竖向刚度对偏心辊轴摩擦摆系统隔震性能影响研究［J］.建筑科学，2010，27(1):29-32.