NLS次优简化算法及其在单站无源定位中的应用
梅勇兵,南建设
(中国西南电子技术研究所,成都 610036)
NLS次优简化算法及其在单站无源定位中的应用
梅勇兵,南建设
(中国西南电子技术研究所,成都 610036)
为了简化基于外辐射源固定单站无源定位求解算法以用于工程实现,建立了定位原理极坐标模型,给出了极坐标系下非线性最小二乘(NLS)定位算法,根据极坐标系下定位算法的特点,为简化计算,提出了NLS次优简化算法。仿真结果表明,NLS次优简化算法有较好的稳定度和定位精度,为工程实现提供了参考。
单站无源定位;外辐射源;极坐标;非线性最小二乘;次优算法
1 引 言
无源定位对于提供系统在电子战环境下的生存能力和作战能力有重要的作用[1-6]。单站无源定位具有设备量少和系统相对独立等优点。目前,单站无源定位主要利用两种类型的信号:一种是基于定位目标自身辐射的信号,另一种是基于定位目标之外的外辐射源的信号。利用外辐射源可以对低空目标和采用射频隐身技术的目标进行定位,本文主要讨论基于外辐射源的单站无源定位算法。
基于外辐射源的单站无源定位[1]主要是靠定位站的测向信息以及外辐射源信号的直达与经待定位目标散射的时间差来进行定位,定位解为非线性方程。
目前,单站无源定位算法都是非线性滤波问题,主要采用的是扩展卡尔曼滤波算法[1-2]和非线性最小二乘[2-4]。扩展卡尔曼滤波及其他基于动态系统的滤波算法都需要估计动态方程的转移矩阵并进行自适应修正,算法相对复杂。最小二乘算法只需要利用观测方程,通过对非线性的观测方程进行线性化处理,通常采用Taylor级数展开的方法,取一次项进行近似,近似之后的线性方程可以利用最小二乘进行求解。
基于外辐射源的单站无源定位观测到的目标相对定位站的方位角、俯仰角和相对时延,极坐标模型可以避免观测值与坐标值之间的频繁转换。特别是利用多组数据进行定位估计的时候,每组数据都需要进行直角坐标与方位角、俯仰角之间的转换。而采用极坐标模型,仅在有需要时对估计结果进行一次坐标转换即可。另外,NLS定位算法是一个多维寻优的问题,其计算中包含矩阵求逆等矩阵运算,而矩阵求逆工程实现比较困难。
本文根据基于外辐射源固定单站无源定位观测量包含方位角和俯仰角的特点,采用极坐标建立了定位原理的模型;推导出了极坐标系下的非线性最小二乘(NLS)算法;根据极坐标系下NLS算法的特点,提出了NLS次优简化算法,将三维寻优问题简化为一维RLS求解;最后,通过计算机仿真对NLS次优简化算法的收敛速度和定位精度进行仿真验证。
2 基于外辐射源单站定位原理
2.1 定位原理
基于外辐射源单站定位是利用已知外辐射源的信号直接到达定位站与经定位目标散射后达到定位站的时间差信息,以及定位站利用散射信号或目标自身的辐射信号测向来进行定位。
通过测定时间差以及已知外辐射源与定位站的距离,可以确定待定位目标到外辐射源和到定位站的距离和;到两点距离和一定的点分布在以两点为焦点的一个椭球上。因此可以确定,待定位目标在该椭球面上。同时,通过定位站测向可以确定待定位目标在由测得俯仰角和方位角决定的一条示向线上。由上述信息决定的椭圆和示向线的交点就是待定位目标所在的位置(示向线起点为椭球内部焦点,有方向性,故只有一个交点)。
2.2 极坐标模型
设外辐射源A与定位站P之间的距离为d,且定位站测得待定位目标的方位角为θ、俯仰角为 φ,三者空间位置关系如图1所示。

图1 基于外辐源位单站无源定位位置关系图Fig.1 Position relationship of single-observer passive location based on outer radiant point
以定位站P为极坐标原点,P到A的方向0°角方向建立极坐标系,则P的极坐标为(d,0,0)。
设待定位目标O的极坐标为(r,θ,φ),信号到达定位站的时间差为τ,则有如下关系:

式中,c为电磁传播速度。
在极坐标下,O点坐标(r,θ,φ)中的 θ和φ已通过测向获得,故确定目标位置仅需确定PO的距离r。
由式(1)知:

由可观测值(τ,θ,φ)决定。
3 定位NLS求解
3.1 NLS算法
根据第2节内容,且 c常数,为记法简单,定义观测量 y=(cτ,θ′,φ′),其与目标的极坐标 z=(r,θ,φ)有如下关系:
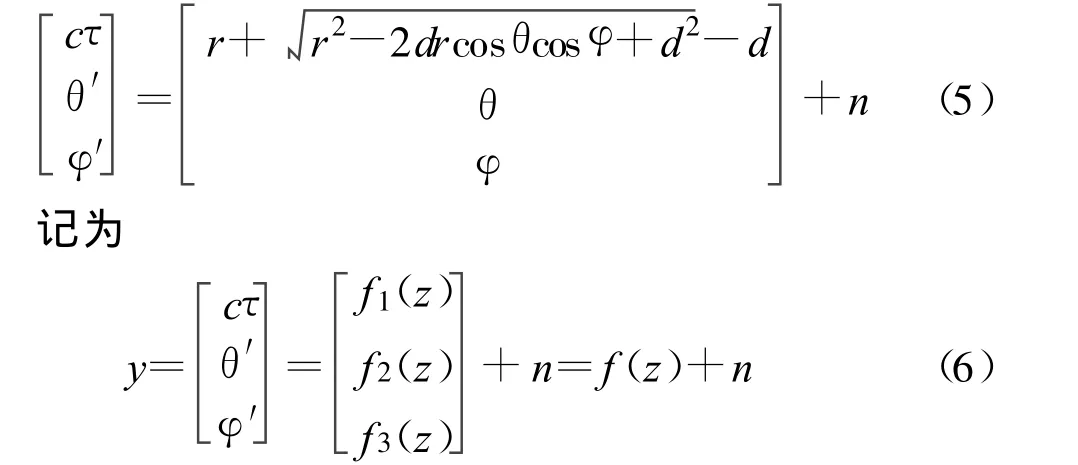
将非线性方程f(z)进行线性化处理,在z0附近泰勒展开,并保留线性部分得到
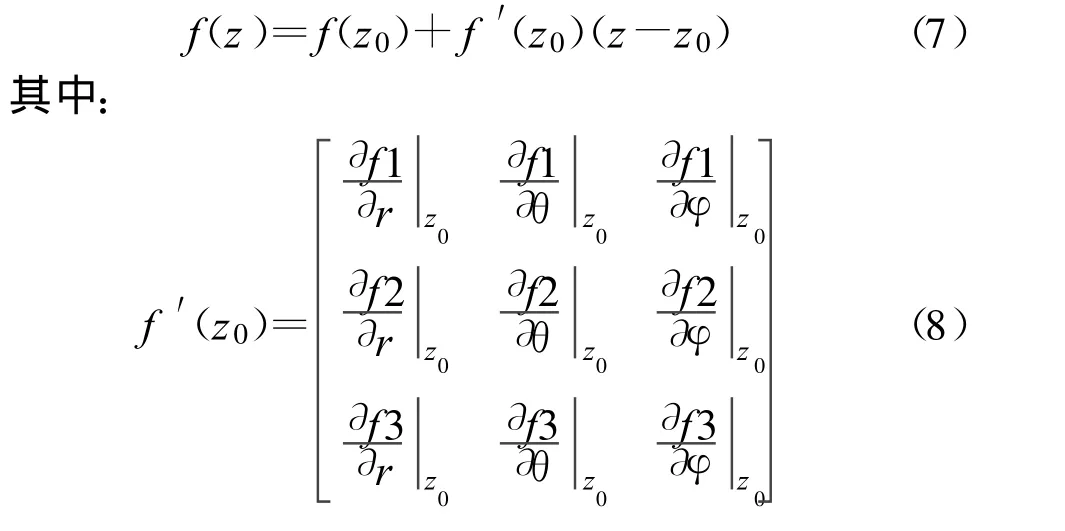
偏导数函数如下:

根据文献[3],式(6)的非线性最小二乘解的迭代形式如下:

式中,N为观测误差协方差矩阵,表达式为
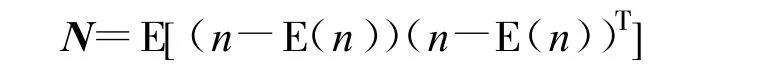
3.2 简化算法
式(10)中,f′(z(k))是矩阵形式,一般情况下不能像递
推
最小二乘一样避免矩阵求逆,用递推方式进行求解。因此,提出一种降维的简化方法,将三维寻优简化为一维交替迭代寻优,降维后的最小二乘可以采用递推最小二乘(RLS)进行计算,进一步简化计算量。
在N=diag(λ1,λ2,λ3)为对角矩阵的时候,即观测量是相互独立的,极坐标模型的NLS算法的目标函数为

(1)对方位角θ进行最小二乘求解;
(2)对俯仰角 φ进行最小二乘求解;
(3)根据 θ、φ的优化结果,对r进行非线性最小二乘求解。
对方位角θ和俯仰角φ的搜索求解可采用RLS算法思想,此时,其第i步新息的权因子为。在完成θ和φ的更新后,作为新的估计值,代入对r进行搜索,可以采用RLS进行计算。
极坐标系下,基于外辐射源的单站无源定位NLS简化算法如下。
(1)初始化

3.3 小结
新提出的NLS简化算法是根据极坐标系下,方位角、俯仰角的观测量与估计量是系数为1的线性关系的特点,将NLS三维寻优的问题简化为一维寻优交互迭代的问题。通过简化,可以避免NLS中矩阵求逆的问题;同时,简化后可以采用RLS方法进行求解,提高稳定度和减少计算量。
简化的NLS方法仅需要将第一次观测作为初始值就可以迭代求解,递推求解过程是采用已经成熟应用于工程的RLS算法实现的,初始值的计算只需要用到完全能工程化的乘加算法,故简化的NLS算法能满足工程实现的要求。
4 仿真分析
设外辐射源与定位站距离150 km,待定位目标初始位置距离定位站81.2 km,方位角1.446 rad,俯仰角0.123 rad。观测时间间隔1 s,假设到达时差测量误差均方差为20 ns,角度测量误差均方差为1°。分别对静态和慢时变目标进行定位仿真。
(1)静态定位仿真
假设目标真实位置在观测时间内部未发生变化或变化可以忽略不计,此时通过公式(4)的计算、采用NLS简化递推算法得到的结果如图2所示。

图2 静态定位仿真结果Fig.2 Location results of static target
从图2可知,NLS简化算法有较快的收敛速度和稳定度,10次迭代之后,距离估计值偏差就在1 km以内,方位角频差在0.005 rad以内,俯仰角偏差在0.008 rad以内。
(2)慢时变目标定位仿真
假设待定位目标在直角坐标系内x轴4 m/s、y轴10m/s、z轴6m/s进行运动,此时通过公式(4)的计算、采用NLS简化递推算法得到的结果如图3所示。
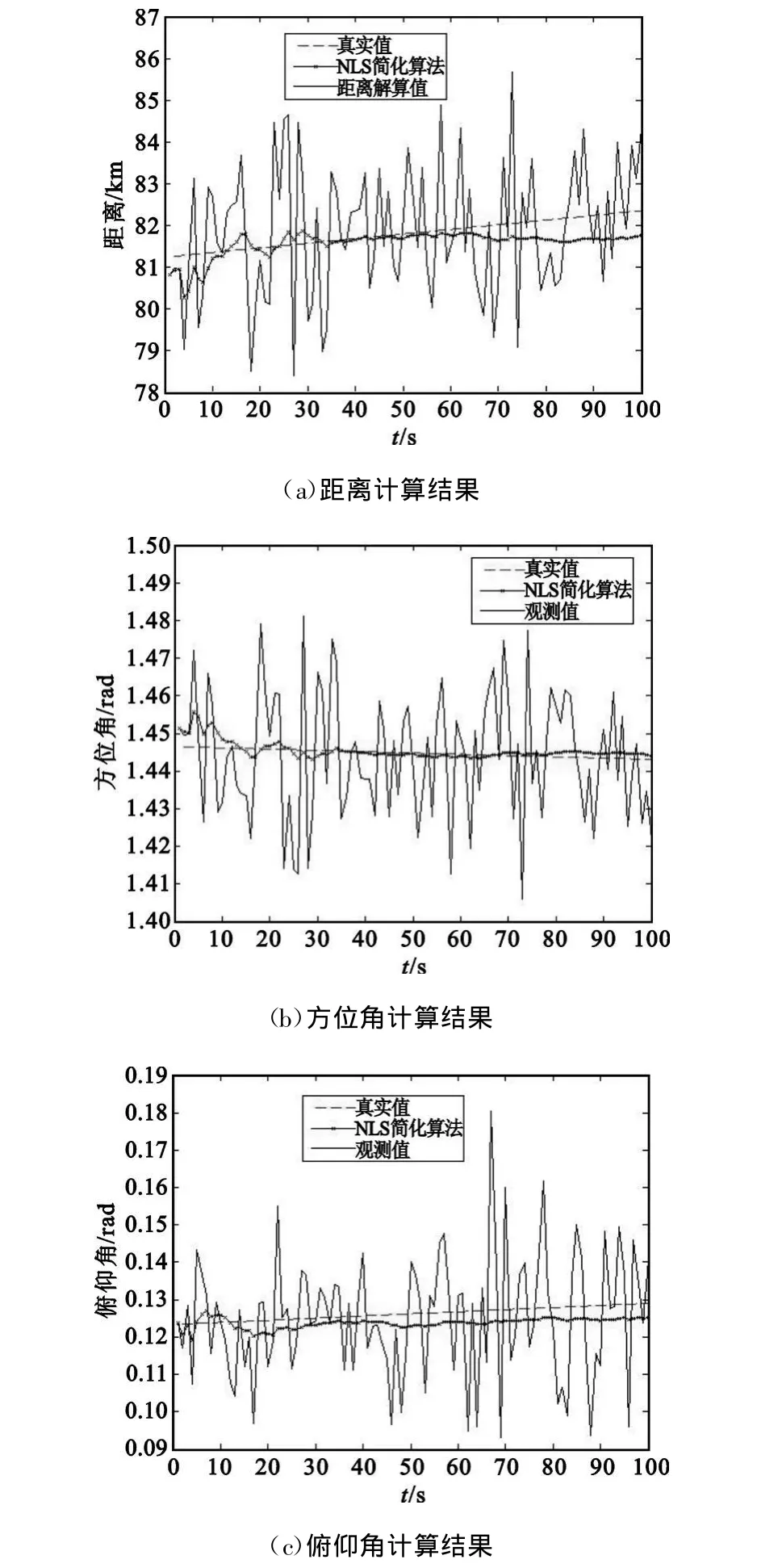
图3 慢时变目标定位仿真结果Fig.3 Location results of slow moving target
从图3可知,对于慢时变目标,NLS简化算法也有较好的收敛效果,但是随着迭代次数的增加,估计结果慢慢偏离真实值,这主要是由于无法跟踪上目标真实位置的变化。
(3)基于初始更新的定位仿真
为了校正偏离,可以采取周期性对NLS简化算法的初始值进行更新的方式,进行定位计算。仿真结果如图4所示。

图4 周期初始化的NLS简化算法结果Fig.4 Location results of low-complexity periodic initialization algorithm
从图4可知,通过周期性初始化NLS简化算法的初始值,能在一定程度上进行偏离校正。
5 结束语
单站无源定位的处理算法比较多,本文从工程实现简单化的需求出发,给出了基于极坐标的非线性最小二乘的简化递推算法,将传统的非线性最小二乘多维寻优简化为一维交替迭代寻优,并利用成熟应用于工程的RLS算法来解决一维寻优的问题。仿真结果表明,极坐标系下NLS简化算法对于慢时变系统有较好的收敛速度与稳定性,可用于基于外辐射源单站无源定位求解,但由于没有目标的状态转移信息,多次迭代后会偏离真实值,本文提出的周期初始化的方法有一定校正能力。简化算法避免了矩阵求逆、向量运算等较复杂算法,对慢时变系统有较好的收敛性和精度,能满足工程实现的要求。
[1]张芹.固定单站无源定位系统的可行性研究[D].成都:电子科技大学,2007.
ZHANG Qin.The Possibility of Single Fixed Observer Passive Location System[D].Chengdu:University of Electronic Science and Technology of China,2007.(in Chinese)
[2]李宗华,冯道旺,周一宇,等.固定单站对三维运动辐射源无源定位算法及可观测性分析[J].信号处理,2004,20(2):117-121.
LI Zong-hua,FENG Dao-wang,ZHOU Yi-yu,et al.Passive Location and Tracking Algorithm for 3-D Moving Emitter By Single Non-moving Observer and Its observability Analysis[J].Signal Processing,2004,20(2):117-121.(in Chinese)
[3]付忠.基于单站的无源定位技术研究[D].成都:电子科技大学,2007.
FU Zhong.The Studies on Single-observer Passive Location[D].Chengdu:University of Electronic Science and Technology of China,2007.(in Chinese)
[4]李悦,柳征,伍渝江.基于非线性最小二乘的三星座时差定位综合算法[J].电讯技术,2010,50(3):27-32.
LI Yue,LIU Zheng,WU Yu-jian.Integration Algorithm of Three-Satellite Constellation TDOA Location Based on NLS[J].Telecommunication Engineering,2010,50(3):27-32.(in Chinese)
[5]廖平,付忠,刘刚.采样滤波算法在单站无源定位中的应用[J].电讯技术,2006,46(4):30-33.
LIAO Ping,FU Zhong,LIU Gang.Application of Sample Filtering Algorithm in Single Observer Passive Location[J].Telecommunication Engineering,2006,46(4):30-33.(in Chinese)
[6]廖平,杨中海,姜道安.基于概率的单站多目标无源定位算法[J].电讯技术,2006,46(1):47-51.
LIAO Ping,YANG Zhong-hai,JIANG Dao-an.A Single Observer Passive Location Algorithm Based on Probability in Multi-target Environment[J].Telecommunication Engineering,2006,46(1):47-51.(in Chinese)
MEI Yong-bing was born in Xinzhou,Hubei Province,in 1979.He received the M.S.degree from Sichuan University in 2005.He is now an engineer.His research concerns signal processing and electronic warfare.
Email:meiybmail@sina.com
南建设(1954—),男,山东沂南人,研究员,主要从事系统总体设计。
NAN Jian-she was born in Yinan,Shandong Province,in 1954.He is now a senior engineer of professor.His research concerns system design.
A Low-complexity Suboptimal NLS Algorithm and its Application in Single-observer Passive Location
MEI Yong-bing,NAN Jian-she
(Southwest China Institute of Electronic Technology,Chengdu 610036,China)
To simplify the algorithm of single-observer passive location based on outer radiant point,the polar coordinate model is built.The algorithm based on nonlinear least square(NLS)algorithm is presented in polar coordinate.To reduce the computation complex of NLS algorithm,a low-complexity suboptimal algorithm is proposed.The simulation results demonstrate the location precision and stabilization of the suboptimal algorithm,which provides reference for engineering realization.
single-observer passive location;outer radiant;polar coordinate;nonlinear least square(NLS);suboptimal algorithm
TN971
A
10.3969/j.issn.1001-893x.2012.06.016
1001-893X(2012)06-0913-05
2012-04-26;
2012-05-11
梅勇兵(1979—),男,湖北新洲人,2005年于四川大学获硕士学位,现为工程师,主要研究方向为信号处理与电子对抗;
——2022 F1意大利大奖赛

