基于LS-SVM的机载天线伺服机构自适应控制

纪 永，李广超

（1.上海建峰职业技术学院 教务处，上海 201900；2.上海大学 电子与信息工程学院，上海 200433）

摩擦力是高性能伺服机构运行过程中需要考虑的重要非线性因素。当伺服机构运行于机载条件下，即所受外力是快时变、变化范围大时，将机载天线伺服机构视为具有参数不确定性的非线性系统就更加必要。传统PID控制方法无法给出满意的控制效果，近年来，控制领域学者已经就此问题提出了各自的解决方法，特别是自适应控制、智能控制等控制方法为参数不确定性的非线性系统提供了新的控制思路等[1-2]。如文献[3]自适应矩阵控制解决伺服系统高速制造运行中电流变化问题，但没有讨论低速率运行条件。文献[4]依据非线性跟踪微分器的基本思想提出一种等效微分估计方法，对摩擦等非线性项的在线估计采用干扰观测器及低通滤波器的方式进行，未论证或证明估计结论。文献[5]采用自抗扰控制器抑制伪线性复合系统中非线性因素的作用，引入扩张状态观测器对不确定性的估计，增加了控制的复杂性，对伺服系统的实时性要求比较高。

在统计学习理论中，Vapnik最早基于结构风险最小化理论提出的支持向量机 （SVM）在充分学习的前提下具备了优越的泛化能力[6]，因此在机器学习领域得到了广泛研究与应用。SVM模型的核心是不等式约束条件下的二次规划问题，求解成本较大。针对这个问题，Suykens提出了最小二乘支持向量机（LS-SVM）。LS-SVM将SVM中的不等式约束条件转换成等式约束条件进行求解，缩减了计算的复杂度，更便于计算机的在线实现。

文中提出一种基于LS-SVM的自适应控制设计方法。此方法将摩擦等非线性特性视为未知项，并利用LS-SVM在线估计被控对象的非线性未知项。文中在利用李雅普诺夫理论论证了闭环系统的跟踪误差一致有界的条件下，设计得到LS-SVM的权向量和偏移量的学习规则。并通过仿真和基于TMS320F2812的数字伺服控制系统上实验，实际运行证明文中结论的正确性和可行性。

1 问题描述

一类单输入单输出系统为：

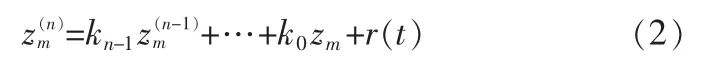
其中，r（t）是有界给定信号，选取合适的参数 ki（i=0，1…，n-1）使得sn+kn-1sn-1+…+k0为Hurwiz多项式。定义跟踪误差e=z-zm，则反馈线性化的控制器为：

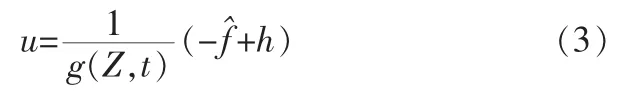
由式（1）、（2）、（3）可得，

图1 离散状态变量构成的自适应系统Fig.1 Adaptive system diagram constructed of discrete state variables

2 LV-SVM控制器设计

LV-SVM是SVM的改进，将传统SVM中的不等式约束改为等式约束，将误差平方和损失函数作为训练集的经验损失，把求解二次规划问题转化为求解线性方程组问题，提高求解问题的速度和收敛精度。

给定 N 个样本组成的样本集如下为{（x1，y1），（x2，y2），…，（xN，yN）}，其中，xi（i=1，2，…，N）为输入向量，xi∈Rn；yi（i=1，2，…，N）为期望值，yi∈R。利用结构风险最小化原则，SVM回归算法采用的估计函数为：

其中，δ（x）为从输入空间到高维特征空间的非线性映射，系数 w，b 由式（6）估计：

其中，‖w‖2为控制模型的复杂度；c为正规化参数，控制对超出误差样本的惩罚程度；Remp为不敏感损失函数。LVSVM将误差平方和损失函数作为优化目标，即式（6）的优化问题转化为：

其中，ξi为松弛因子，其作用是将SVM中的不等式约束转化为等式约束。

近年来电子商务发展迅速，网上购物逐渐成了消费者主要的购物方式。电子商务的发展带动了物流产业的飞速发展，建设自动化、网络化、可视化、实时化、跟踪与智能控制的现代物流系统是当代智慧城市发展的必要条件。佳木斯的广源物流园区、新纪元物流园区等物流区域里的很多企业将RF、条形码、GPS等物流技术应用于企业管理运营中，取得了良好的效果。也为智慧城市的建设作出贡献。

为了求解该优化问题，引入拉格朗日函数：

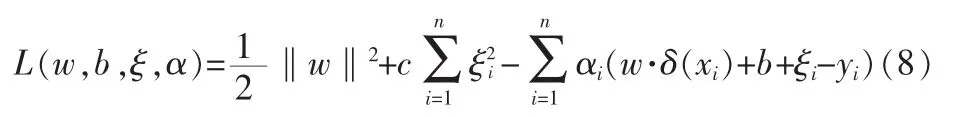
其中，αi（i=1，2，…，n）为拉格朗日乘子。

函数L应对w，b，ξ，α求最小值，即优化条件为：

从而

构造函数K（xi，xj）=0，使问题转化为求解如下线性方程：

其中，y=[y1，y2，…，yN]T∈RN，I=[1，1，…，1]T∈RN，α=[α1，α2，…，αN]T∈RN，I∈RN×N为单位阵，H∈RN×N为方阵， 其中 Hij=K（xi，xj）=δ（xi）·δ（xj），∀ij=1，2，…，N，其中 K（·，·）为核函数，它是 δ（xi）和 δ（xj）的内积。 任何满足 Mercer条件的函数，都可作为核函数，采用不同的函数作为核函数可以构造实现输入空间中不同类型的非线性决策面的学习机器。最常用的核函数有多项式函数K（xi，xj）=（xi·xj+1）d，RBF函数K（xi，xj）=exp（-‖xi-xj‖2/2σ2），Sigmoid函数K（xi，xj）=tanh（b（xi·xj）+c）等。

通过式（10）求解α，b，并进一步求解出w。

LS-SVM的函数估计为：

LV-SVM控制器设计步骤如下：

1）离线理论设计计算，得到并选取合适的参数ki（i=0，1，…，n-1）使得sn+kn-1sn-1+…+k0为Hurwiz多项式。选取合适的对称正定矩阵R，Q，并求得正定矩阵P。

2）对机载天线伺服机构输入合理的输入值或随机值，以便产生丰富的输入输出数据。基于交叉验证方法选取核参数和正则化参数，对LS-SVM进行离线训练，得到初始值。

3）利用式（11）在线自适应调整相关参数。使机载天线伺服机构在线稳定地跟踪任何光滑的输入信号。

3 设计应用与结果分析

文中的设计方法在某型正在研制的机载天线伺服机构的控制系统设计采用。此机载天线伺服机构实质上是一种小型的两轴伺服稳定跟踪平台，可以实时采集、输出天线的姿态角，并可以按照任务计算机的指令控制天线的姿态指向。它的组成为：控制器、精密电位器、速率陀螺、直流力矩电机、电机驱动模块、二次电源、导电环、连接母板等组成。为了简化试验，暂不接入速率陀螺，仅使用精密电位器作为测角部件。电机及框架等试验参数如下：Ra=0.55 Ω，Cm=3.3 Nm/A，Ce=0.9 V/（rad/s），J=1.1 kg·m2；由于本载天线伺服机构控制系统包括方位、俯仰两轴两通道和其它指令性功能等的实时控制，故数据分析方法为将微处理器所采集所到实时位置信息经由RS422与计算机通讯，这样既可以从计算机接收控制指令，也可以将实时的运行数据传送给计算机，最后将计算机中所记录记录的离线数据导入到MATLAB环境。这样可以在计算机上可以方便地观察运行结果和进行结果分析。

以某机载天线伺服机构的方位角为例，讨论LV-SVM控制器的设计。通过改变方位角的直流电机的电压u可以控制天线伺服机构方位角度值z，代入式（1）得到伺服机构控制系统模型为：

设定方位角初始位置值为 z（t）=0°，参考输入值为 r（t）=2°。摩擦力视为有界未知项，根据离线测量，此伺服机构控制系统中，摩擦力折算到控制电压值后小于0.3 V。按前文所述的LV-SVM控制器的设计步骤，取控制系统的输入为x=[z z˙]T，输出为f^，进行离线训练，得到LS-SVM的参数初始值，再进行在线自适应控制。图2为经典PID控制器方位角位置运行图，图3为LV-SVM控制器方位角位置运行图。分析实验结果可知：基于LS-SVM的机载天线伺服机构自适应控制器比经典PID控制器取得更好地控制效果，能够在线稳定地跟踪包括阶跃信号在内的任何光滑的输入信号，同时补偿摩擦等非线性特性，改善系统的动态品质和静态特性。。

图2 经典PID控制器方位角位置运行图Fig.2 Azimuth position operation diagram of the classical PID controller

4 结束语

图3 LV-SVM控制器方位角位置运行图Fig.3 Azimuth position operation diagram of the LV-SVM controller

从某机载天线伺服机构的测试结果和实际控制系统对天线目标的定位可以得到如下结论：1）在机载天线伺服机构运行条件为所受外力是快时变、变化范围大、且自身摩擦等非线性特性不能忽略，如果忽略并采用经典PID控制器的设计方法，会使得控制系统的性能无法满足精度跟踪需要。2）摩擦力作为伺服机构固有非线性特性的一种，其有界、光滑等特点，使得本文假设的前提存在，为LS-SVM自适应控制器设计提供可能。3）LS-SVM将SVM中的不等式约束条件转换成等式约束条件进行求解，缩减了计算的复杂度，完全能够使用计算机的在线实现。目前文中控制器设计方法已成功运用于某型某机载天线伺服机构的控制系统，具有实用意义。重复试验结果表明该方法正确、可靠。

[1]Kima H M，Park S H.Precise friction control for the nonlinear friction system using the friction state observer and sliding mode control with recurrent fuzzy neural networks[J].Mechatronics，2009，19（2）:805-8152.

[2]Wai R J，Chang J M.Intelligent control of induction servo motor drive via wavelet neural network[J].Electric Power Systems Research，2002，62（1）:67-76.

[3]Wang D，Li C.Self-Adaptive dynamic matrix control for high-speed machining servo control[J].Journal of Machine Learning Research，2003（21）:733-738.

[4]田大鹏，吴云洁.高精度电机伺服系统控制综合方法[J].电机与控制学报，2010，14（7）:66-74.TIAN Da-peng，WU Yun-jie.Synthesis methods of high precision motor servo system control[J].Electric Machines and Control，2010，14（7）:66-74.

[5]刘国海，张懿.基于自抗扰控制器的两电机变频调速系统最小二乘支持向量机逆控制[J].中国电机工程学报，2012，32（6）:138-145.LIU Guo-hai，ZHANG Yi.Least squares support vector machines inverse control for two-motor variable frequency speed-regulating system based on active disturbances rejection[J].Proceedings of the CSEE，2012，32（6）:138-145.

[6]DONG Jia-xiong，Krzyzak A，Suen C Y.Fast SVM training algorithm with decomposition on very large data sets[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2005，27（4）:603-618.