基于多回路模型的双馈异步发电机匝间短路故障检测方法研究

钱雅云，马宏忠，张志新，程 俊，王安其

（河海大学 能源与电气学院，南京 210098）

前言

双馈异步发电机是目前风力发电系统的主流机型，其单机容量大，价格昂贵。运行实践表明，定子绕组匝间短路故障往往导致相间短路或接地短路故障，并且该类故障的发生概率高达 30%[1]，因此必须对双馈异步发电机的定子绕组匝间短路故障的瞬变过程进行研究并提出检测方法。

多回路理论和磁导分析法[2,3]在交流电机绕组故障分析领域有着广泛的应用。文献[4,5]采用该理论对异步电动机进行内部故障仿真分析，并提出负序电流、零序电压等故障检测方法。本文基于多回路理论，推导了绕线型双馈异步电机在正常情况和定子绕组匝间短路故障下的数学模型，并进行仿真分析。仿真结果表明，可以采用定子电流负序分量来检测定子匝间短路故障，但是负序电流受到负载情况的影响可能会导致误判。在此基础上，本文提出了负载系数的概念，并根据当前电机的负载状况确定适当的负序电流阈值用于检测故障。

1 多回路数学模型

1.1 双馈异步电机定转子回路

双馈异步电机定子三相绕组可以采用图1所示的三种接线方式，实际应用中多采用 YN型接线方式。其转子绕组与定子绕组相同，也为YN型接线。

1.2 电机在正常情况下的基本方程

根据图1可以推导出正常情况下双馈异步电机的基本方程式：

式中：MT 、LT分别是电磁转矩和负载转矩；U、I、R、M分别是定转子三相电压、电流、回路电阻和各相自感系数、相间互感系数。

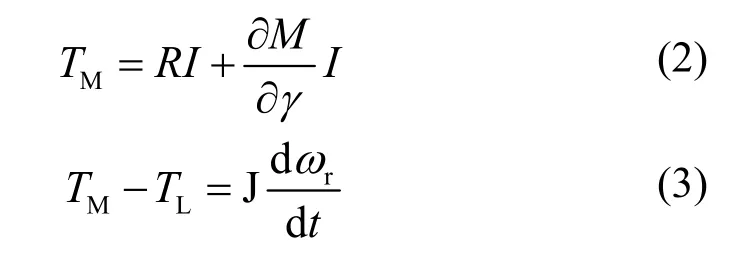
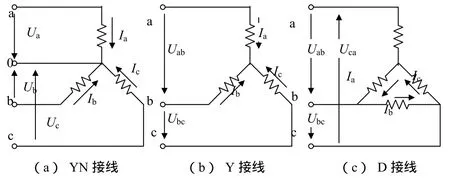
图1 电机接线方式

1.3 电机在定子匝间短路故障情况下的基本方程

当定子绕组出现匝间短路故障，假设该故障发生在定子A相绕组，则其示意图如图2所示。

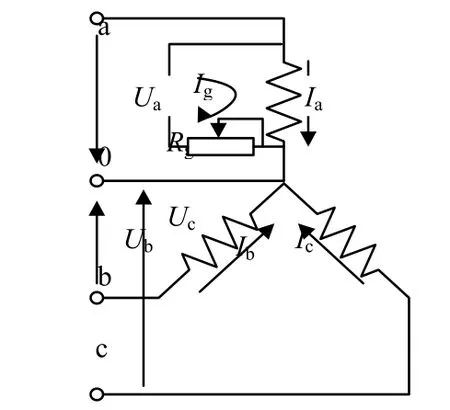
图2 定子匝间短路故障示意图

由该示意图显然可见，定子侧增加一个新的回路，即为匝间短路回路。此时，定子A相的电压方程也发生变化。匝间短路回路方程以及定子A相电压方程如下：

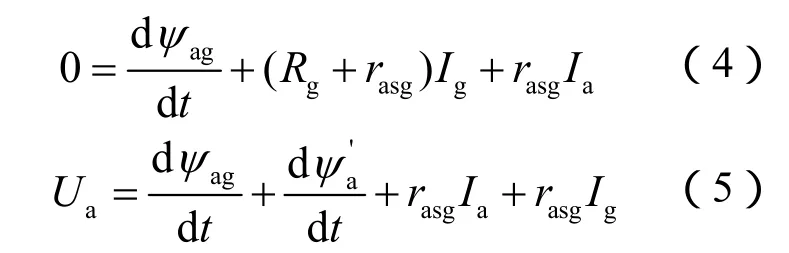
式中：ψag、rasg分别为定子A相绕组匝间短路环磁链和电阻；为定子A相绕组匝间短路故障后（不包括匝间短路环）磁链，相应的矩阵 U、I、R、M 也发生相应变化，此处不一一列举。

2 仿真结果分析

按照上述多回路数学模型，对一台额定容量为3kW的绕线型双馈异步电机进行数字仿真。图3表示半载条件时正常电机、定子A相绕组2匝、4匝和8匝匝间短路情况下的定子电流。

图3 定子电流仿真结果

从上述仿真结果可以看出，该模型均可以准确反应双馈异步发电机的运行状况；随着故障严重程度的增加，定子电流的不对称性增加，电流中出现其他电流分量。相关研究表明，异步电动机发生定子绕组匝间短路故障后，在其定子电流中将出现负序分量[6]。

3 负序电流检测法

3.1 负序电流产生机理

负序电流的产生机理通常从附加电流源角度来分析[7]，此处从电磁感应角度来分析。正常情况下，电机定子三相绕组磁动势为一正转圆形磁动势，在三相对称绕组中感应正序电流；当定子绕组发生匝间短路故障时，等效为在短路匝上叠加一电流分量。该叠加电流的磁动势为一脉动磁势，它可以分解为两个幅值相等、转速相同但是方向相反的圆形旋转磁动势。其中，正转圆形磁动势在定子三相绕组中感应正序电流、反转圆形磁动势在定子绕组中感应负序电流。

3.2 负序电流的检测

基于上述负序电流产生机理，采用对称分量法[8]编程求取负序电流。图4~6分别表示空载、半载及满载时电机发生定子A相匝间短路后的负序电流。

对上述结果进行分析，可以得出以下结论：

a. 正常情况下双馈异步电机起动时，定子电流中将出现很小的负序分量但迅速衰减为0，经分析可知，该分量是由于电机在起动时处于暂态所产生的。

b. 双馈异步电机在发生定子绕组匝间短路故障后，定子电流中将出现负序分量，其数值伴随着故障严重程度的加剧而明显增大。

图4 电机空载情况下定子负序电流

图5 电机半载情况下定子负序电流

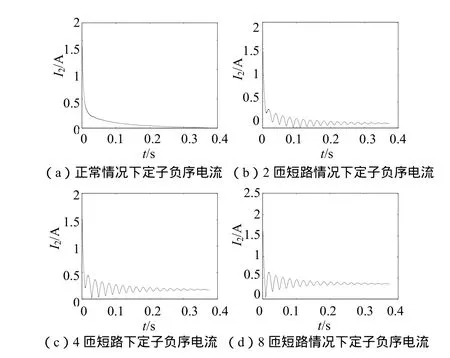
图6 电机满载时各种运行情况下定子负序电流

c. 双馈异步电机发生定子绕组匝间短路故障，在相同形式的匝间短路故障下，负序电流值随负载增加而微弱增长。

d. 就理想电机而言，定子绕组匝间短路故障特征明显，因而可以通过负序电流值变化来实现故障检测。

e. 就实际电机而言，由于制造工艺及安装等原因，定子绕组不可能做到完全的三相对称，从而使得定子电流中仍然存在负序电流且伴随着负载增加而增加。因此在进行定子匝间短路故障检测时，应将负载情况考虑进去，设定合适的检测阈值，以避免误判。

4 检测阈值

4.1 负序电流量化

本文引入负序电流的有效值来量化负序电流，表1是空载、半载以及满载时各种故障情况下负序电流的有效值。

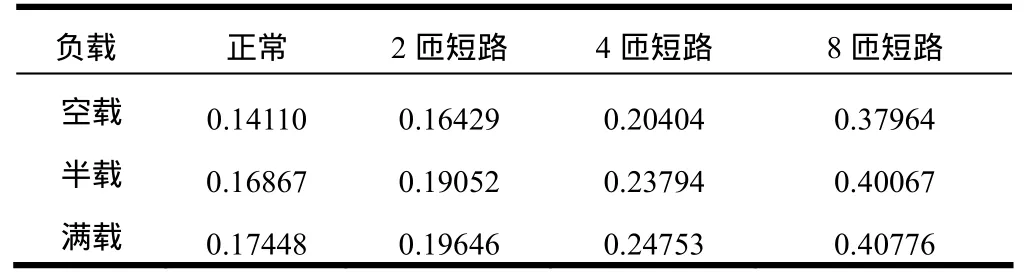
表1 不同负载各种运行状态下的负序电流有效值(A)

由表1可以看出负序电流有效值随着故障严重程度明显增加，且随着负载增加而微弱增加。除此以外，电机满载正常运行的数值比空载时2匝匝间短路情况下的数值大，如果不考虑负载情况，仅简单地设定一个定值作为检测阈值，就很有可能会导致误判。

4.2 负载系数

为了解决上述问题，此处引入负载系数LK 以获得不同负载条件各自对应的检测阈值。负载系数定义为各负载条件下电机定子故障相负序电流有效值与空载条件下正常电机的负序电流有效值的比值。由表1可以得到空载条件下电机正常运行时的负序电流检测阈值为0.14110±0.005 A。负载系数LK 的确定方法如下：首先，以 20%负载间隔求出空载至满载条件下电机在正常情况、2匝短路、4匝短路、8匝短路下的负序电流有效值；接下来依次求出以上各有效值之比的平均值；最后对得到的5组数据采用数据拟合的方法来确定负载系数LK ，各负载情况L对应的检测阈值就等于正常电机空载情况下的负序电流有效值与负载系数KL的乘积。

经拟合，最终得出的负载系数 KL与负载L呈三次多项式的关系，拟合结果如图7所示。

4.3 误差估计

根据拟合所得的负载系数和空载负序电流有效值，推算出30%负载、半载、70%负载条件下电机正常运行时的负序电流有效值的检测阈值，并进行误差分析，见表2所示。

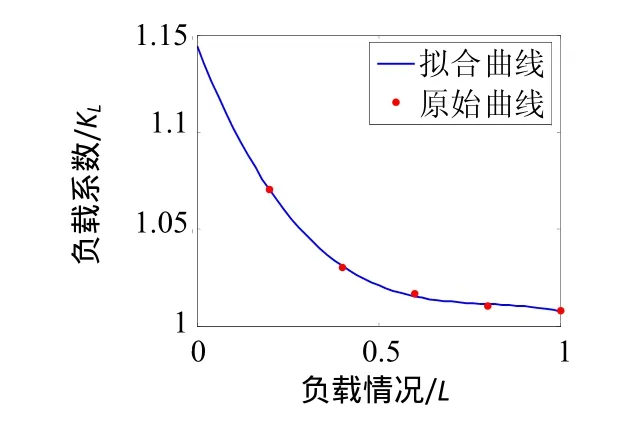
图7 负载系数拟合图

表2 检测阈值误差分析

由上表可知，采用负载系数和空载有效值来共同设定检测阈值的误差均小于 0.15%，因此采用该方法来设定检测阈值。对于其他类型电机，当采用与电流相关的特征量来诊断匝间短路故障时，也可以引入该系数，计算出对应的表达式以考虑负载对电机故障诊断的影响。

5 结论

首先，导出了双馈异步发电机多回路模型，对电机正常和故障情况进行仿真，提出负序电流有效值作为故障特征量来检测故障的严重程度。

在对负序电流检测阈值的设定过程中，得出以下结论：必须充分考虑负载对负序电流的影响，否则会引起故障误判。为此本文引入负载系数，通过数据拟合确定负载系数的表达式并进行误差估计，误差分析表明，通过该方法来确定检测阈值是有效可行的。

[1]IAS Motor Reliability Working Group. Report of Large Motor Reliability Survey of Industrial and Commercial Installations, Part1[J]. Industry Applications, IEEE Transactions on, 1985, 21(4):853-872.

[2]高景德, 王祥珩, 李发海. 交流电机及其系统的分析[M]. 北京: 清华大学出版社, 1993.

[3]宁玉泉. 鼠笼感应电机转子断条和端环开裂的故障诊断和参数计算[J]. 中国电机工程学报, 2002,2(10): 97-103.

[4]马宏忠. 电机状态监测与故障诊断[M]. 北京: 机械工业出版社, 2008.

[5]许伯强. 异步电动机绕组故障分析及其检测方法研究[D]. 北京: 华北电力大学, 2002.

[6]欧阳帆, 周有庆, 郭自勇. 基于平衡变压器的电流平衡补偿方[J]. 电工技术学报, 2007, 22(5):53-57.

[7]许伯强, 孙丽玲, 孙俊忠. 异步电动机定子故障检测新算法[J]. 电力自动化设备, 2008, 28(10):14-18.

[8]孙宇光, 王祥珩, 欧阳蓓, 等. 凸极同步发电机定子绕组内部故障的瞬态计算及有关保护方案的分析[J]. 电工技术学报, 2001, 16(1): 3-8.