一种拓展的面向删失样本的支持向量回归模型

尤明懿

（1.中国电子科技集团公司第三十六研究所，浙江 嘉兴 314033；2.上海交通大学机械系统与振动国家重点实验室，上海 200240）

0 引言

从20世纪90年代中期开始，支持向量机（SVMs：Support Vector Machines）一直受到研究人员的极大关注。支持向量机通常可用于分类[1]、排序[2]、概率分布估计[3]与回归分析[4]。

在回归分析领域，支持向量回归模型（记作SVR模型）通常处理数据集（xi，yi）ni=1，其中yi是样本i的精确值，xi是相应的特征量。然而，在一些应用领域，目标精确值通常无法获得，取而代之的是一个包含精确值的区间（li，ui），其中li、ui分别是区间的上下界。相应地，数据集（xi，yi）ni=1就变为（xi，li，ui）ni=1。由于删失机制，这样的数据在生存分析和可靠性试验中很常见[5-6]。通常有3类删失，即区间删失（此时li和ui均为有限值），右删失（此时li为有限值，ui为正无穷）和左删失（此时li为负无穷）。

为了使支持向量回归模型能处理类似（xi，li，ui）ni=1的数据集，Shivaswamy等[7]提出了一种新的支持向量回归模型（记作SVCR模型）。SVCR模型与SVR模型形式类似，但可以处理删失样本。在文献 [7]中，作者比较了训练集中有50%样本为删失样本至训练集中有99.5%样本为删失样本的情况下，SVCR模型和传统SVR模型的表现。结果显示，当训练集中删失样本的比例较高时，SVCR模型的表现显著优于传统SVR模型的表现。此外，基于对5个生存分析数据集的分析结果，SVCR模型对测试样本精确值的估计也优于传统的统计模型（如：韦伯模型、对数正态分布模型）。本文即致力于对SVCR模型的拓展。

1 SVR和SVCR模型简介

本节介绍SVR与SVCR模型，以更好地理解本文提出的拓展模型。为简便计，本节仅考察线性SVR和SVCR模型并比较它们的区别。更复杂的核化（kernelized）SVR和SVCR模型与计算时间等考虑可参考文献 [4，7]。

给定数据集（xi，yi）ni=1，回归的问题即寻找一个m维空间至一维空间的映射函数f：Rm→R，使其对于变量xi较好地拟合目标值yi。当函数f为线性函数，即f=wTx+b时，线性SVR模型为：

ξi和为非负中间变量。

从式（1）中可以发现SVR模型仅处理单值对象yi。SVR处理含删失样本的数据集的简单方法是仅考虑数据集中的单值样本，而忽略删失样本。更具体地， 即给定数据集（xi， li， ui）ni=1， SVR模型仅使用li=ui的样本来估计参数w和b。为利用删失样本的潜在信息，Shivaswamy等[7]提出一个SVCR模型，即：

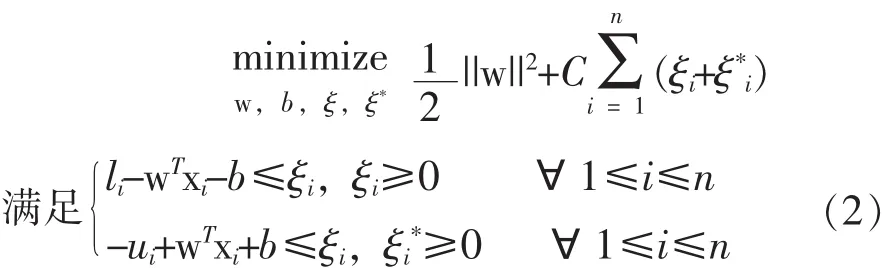
式（1）中，SVR模型使用了称为 “ε不敏感”损失的损失函数，即：

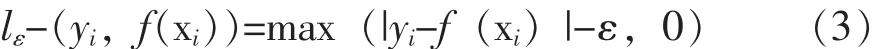
式（2）中采用的损失函数为：

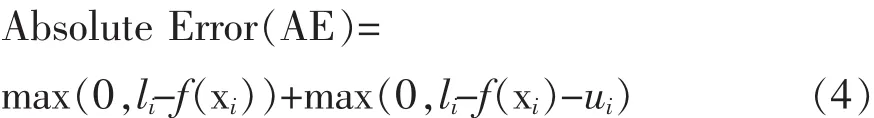
使用式（4）中的损失函数，如果拟合函数的输出大于li或小于ui则给予惩罚。在li=yi=ui的特殊情况下，式（4）变为：

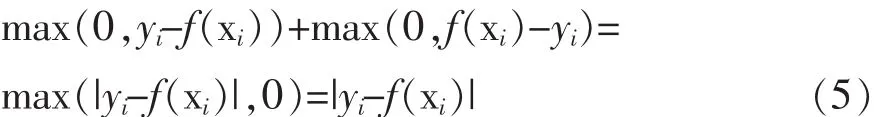
式（5）中的损失函数即为最小模（least-modulus）损失函数，它对未知的噪声模型是鲁棒的[8]。继承了这个性质，式（3）中的 “ε不敏感”损失有一些额外的性质，总结如下：

a）它是最小模损失的推广，即：当ε=0时，“ε不敏感”损失即为最小模损失。因此，通过选择最优的ε值，使用 “ε不敏感”损失函数的回归模型的泛化性能至少和使用最小模损失的回归模型一致。

b）通过定义ε可控制模型复杂度[9]。ε直接影响Vapnik-Chervonenkis（VC）维度，且该损失函数相对有限样本的内在变化是鲁棒的。

c）它赋予了支持向量回归模型稀疏性的性质[8]。通常，一个较大的值对应于较少的支持向量，因而所需的计算时间较少，这对于数据量大的问题是十分重要的。

d）它使用户能够自定义一个能接受的精确度[10]。

因此，如果找到一个继承了 “ε不敏感”损失函数优点的式（4）中损失函数的拓展版本，使用新的损失函数的SVCR模型（记作ε-SVCR模型）有望更精确地进行目标值估计。

2 ε-SVCR模型

本节介绍ε-SVCR模型。首先引入损失函数：max（0，（li-ε）-f（xi））+max（0，f（xi）-（ui+ε））（6）为直观起见，图1比较了SVR、SVCR和ε-SVCR模型的损失函数（分别记作Loss 1、Loss 2和 Loss 3）。

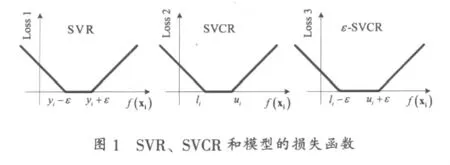
如图1所示，ε-SVCR模型的损失函数（Loss 3）可以视为SVCR的损失函数（Loss2）的推广，两者在ε=0时等价。此外，当li=ui时即目标的精确值已知时，ε-SVCR模型的损失函数等价于SVR模型的损失函数（Loss 1）。

对照式（2），下面给出ε-SVCR模型的数学表达：

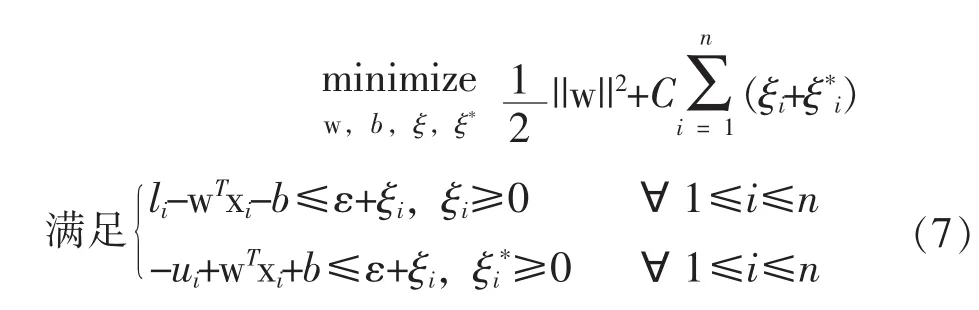
SVR模型流行的一个重要原因是线性SVR模型可以经过核化（kernelization）推广至非线性回归模型。通过使用某种映射函数 ：Rm→H将xi映射至希尔伯特空间H，SVR模型在空间H中进行回归计算，因而可给出变量xi所在的输入空间的任意复杂的函数。与SVR模型一样，ε-SVCR模型也可进行核化，则式（7）变为：

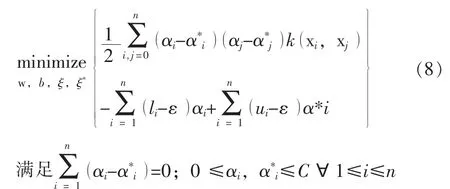
αi和为模型参数。

通过解式（8）可获得αi和的最优值，则在输入空间x处的目标值可估计为：

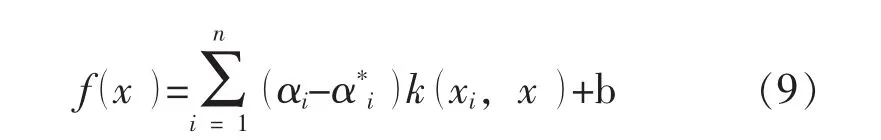
值得指出的是， 通常仅一小部分（αi-）为非零值。

3 对比试验

本节开展一个对比试验以比较SVR、SVCR和ε-SVCR模型的表现。原来的包含252个非删失样本（即样本精确值已知）的回归数据集来源于StaLib[11]。选择其中的一半作为训练集，而将剩余的作为测试集。为研究从无删失样本到大部分样本（如：95%）为删失样本的情况下，SVR、SVCR和ε-SVCR模型的表现，将训练样本中的 η%调整为对目标精确值的区间删失，其中η值如表1所示。

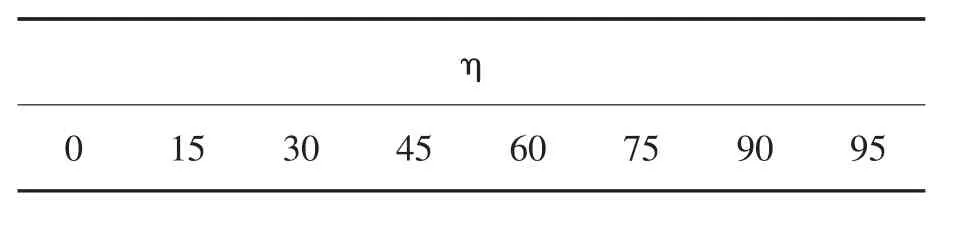
表1 η值

本文将目标精确值调整为区间值的方法，即将目标精确值si转换为区间（li，ui），其中：

式（10）中：σ——训练集中目标精确值的标准差；

δi——服从标准正态分布的随机值。

考察各个η值情况下，SVR、SVCR和 ε-SVCR模型在估计测试集中目标精确值时的表现，共得24组测试结果。

对于SVR、SVCR和ε-SVCR模型采用相同的训练、模型选择和测试过程。在每个训练和模型选择过程中，均选择在一个5段交叉校验过程中最小化平均绝对误差（average absolute error）的模型参数。对应于式（4），平均绝对误差定义为：

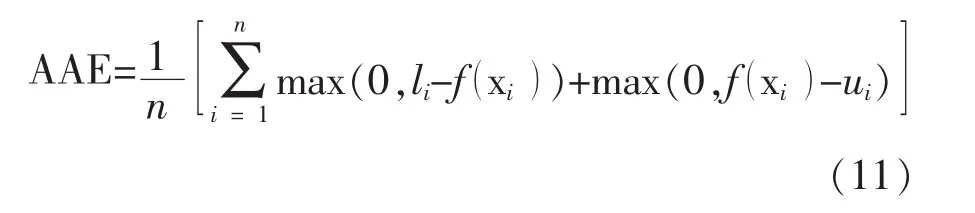
值得指出的是，SVR、SVCR和ε-SVCR模型训练集的区别是：SVCR和ε-SVCR模型使用所有的训练样本，而SCR模型仅采用训练集中目标绝对值已知的样本（即：li=ui）。之后，采用测试集中的样本测试所训练的模型，并得到每个训练样本的绝对误差（即：式（4）定义的AE）。使用多项式和高斯核函数的SVR、SVCR和ε-SVCR模型的测试样本预测误差盒形图如图2和3所示。

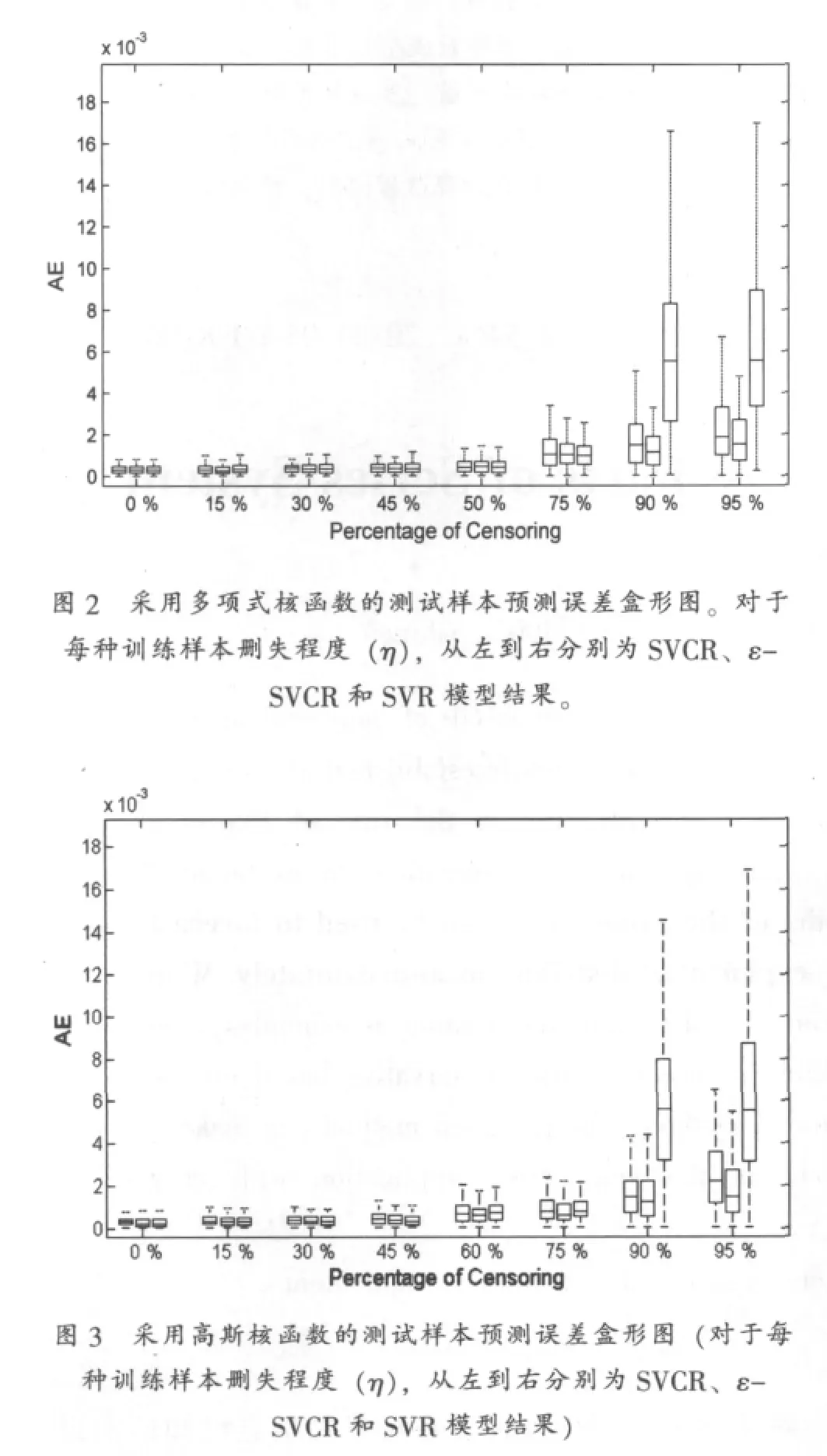
图2和3中的结果显示，当较大（≥90）时，SVCR模型的表现显著优于SVR模型的表现，而当η较小（≤75）时两者的表现区别不大。这与文献 [7]中的结论一致。此外，从图2和3中可以观察到，ε-SVCR模型的表现始终优于SVCR模型的表现；在η较大（≥90）时，改善比较显著。

4 结论

本文提出一个面向删失样本的ε-SVCR模型。通过采用一种新的 “ε不敏感”损失函数，相对于SVCR模型，ε-SVCR模型的表现有所提升，这种提升在训练样本中删失样本较多时尤为显著。通过在生存分析和可靠性试验中采用ε-SVCR模型。可以期望通过挖掘删失样本的信息以获得更精确的目标值估计。

致谢

作者感谢P.K.Shivaswamy提供的SVCR模型计算平台[12]。

[1]BURGES C.A tutorial on support vector machines for pattern recognition[J].Data Mining and Knowledge Discovery， 1998，（2）： 121-167.

[2]CHU W， KEERTHI S S.Support vector ordinal regression[J].Neural Computation， 2007， 19:792-815.

[3]VAPNIK V， MUKHERJEE S.Support vector method for multivariate density estimation[M].USA:MIT Press， Advances in Neural Information Processing Systems，2000:659-665.

[4]SMOLA A， SCHLKOPF B.A tutorial on support vector regression[J].Statistics and Computing， 2004， 14:199-222.

[5]MEEKER W Q， ESCOBAR L A.Statistics Methods for Reliability Data[M].New York： Johm Wiley&Sons.Inc.，1998.

[6]KALBFLEISCH J D， PRENTICE R L.The Statistical Analysis of Failure Time Data[M].New York： Johm Wiley&Sons.Inc.， 2002.

[7]SHIVASWAMY P K， CHU W， JANSCHE M.A support vector approach to censored targets[C]//ICDM’07:Proceedings of the 17th IEEEE International Conference on Data Mining， 2007： 655-660.

[8]VAPNIK V.The Nature of Statistical Learning Theory[M].USA:Springer， 1999.

[9]CHERKASSKY V， MUIER F.Learning from Data:Concepts， Theory， and Methods(second edition).New York：Johm Wiley&Sons.Inc.， 2007.

[10]PARRELLA F.Online Support Vector Regression[M/OL].Available at:http://onlinesvr.altervista.org

[11]Dataset available at:http://lib.stat.cmu.edu/datasets/bodyfat

[12]Code available at:http://www1.cs.columbia.edu/～pks2103/publications.html