基于改进人工鱼群算法的含风电场电力系统最优潮流计算

洪彬倬，聂一雄，盛 丹，武小梅

（广东工业大学 自动化学院，广东 广州 510006）

风能是一种非稳定的能源，其具有随机性和间歇性.从电网侧来看，风电场相当于一个具有随机特性的扰动源，它们的接入会对电网产生一定的负面影响，如电压闪变、谐波污染［1-2］等.此外，风电场接入系统后还会改变电网原有的潮流分布及功率的传输.随着风电场的规模及其在系统所占比例的增大，对系统产生的影响也越来越严重，对系统经济运行也提出了更高的挑战，研究风电接入后对系统潮流的影响具有重要意义.

经典算法和智能算法是作为最有潮流优化算法的两种类型.经典算法以简化梯度法、牛顿法、内点法等［3-4］为代表，其特点是利用目标函数对控制变量进行梯度求导形式进行求解，易于陷入对局部最优解求解的陷阱.智能算法包括遗传算法、混沌优化算法、粒子群优化算法等［5-7］.智能算法与导数无关，易于跳离局部极值点，且算法本身计算行为方式具有并行性，极大地提高了对大规模非线性优化问题的计算速度.

人工鱼群算法作为以动物群体行为为基础的现代智能算法，算法的随机寻优方式主要是模仿了鱼群的行为，通过对鱼的聚群、觅食和追尾行为的模仿，从鱼的底层行为进行构造，达到突出各个体鱼的个体最优从而突出全局最优的目的.

1 最优潮流数学模型

电力系统最优潮流计算为典型的多约束非线性规划问题的求解，其数学模型为

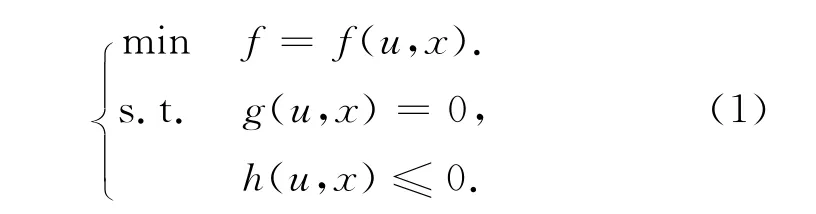
式中x是状态变量的集合；u是控制变量的集合；g（u，x）为等式约束；h（u，x）为不等式约束.

系统每一节点的注入有功功率和无功功率都需满足：

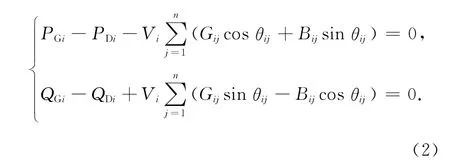
式中i∈ND，ND为系统所有节点集合.

并且方程的不等式约束：

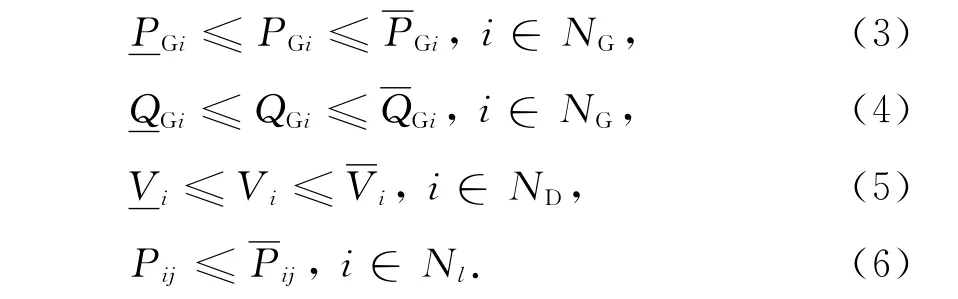
式中 上、下标表示变量取值的上、下限，PGi，QGi表示发电机有功及无功出力；PDi，QDi分别表示节点有功及无功负荷；Vi，θi分别为电压幅值与相角；Pij表示线路潮流限制；Nl为系统所有线路集合.

在实际系统中，用户端的负荷不断变动，为一个随机变量.为了尽可能地贴近实际应用，笔者假设负荷服从正态分布，用随机变化量D表示.风电场的出力是一个随机变化量，引入随机变量w表示.以

表示所有随机变量，则式（1）可表示为

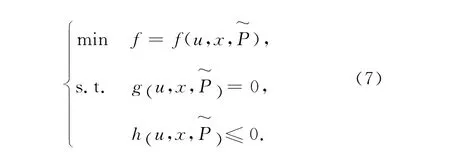
式（2）可表示为

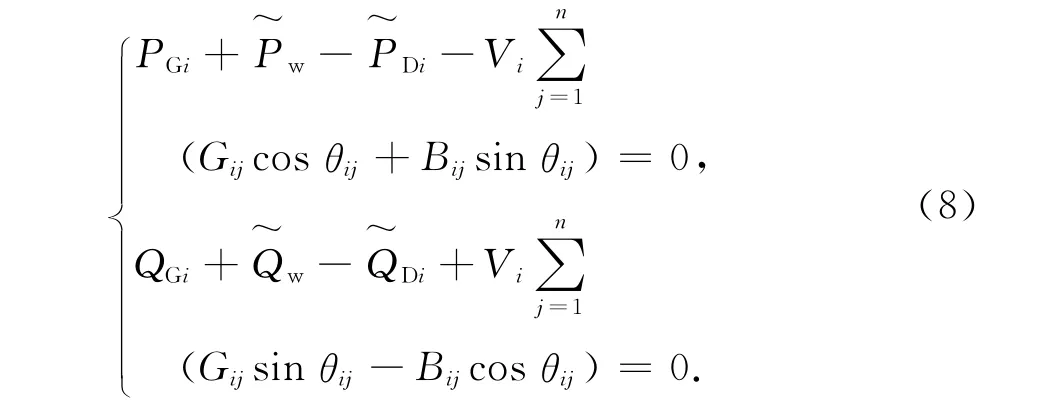
由于风速具有随机性，故可通过公式生成，即

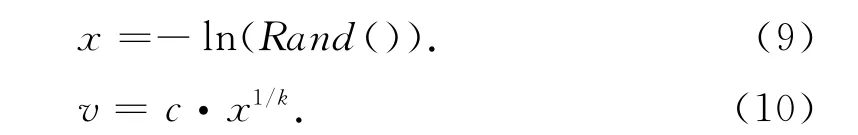
式（9）、（10）中Rand（）为计算机内部提供随机函数，取值范围为（0，1）；c和k分别为风电场的形状参数和规模参数.

则风机输出功率可由公式所得，即

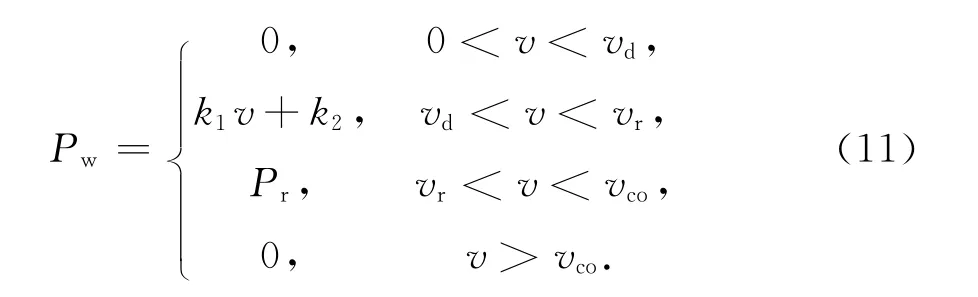
式中k1＝Pr／（vr-vci），k2＝-k1／vci；Pr为额定功率；vd为切入风速；vco为切出风速；vr为额定风速.

笔者设风电场出力为PQ节点，则其从系统中吸收的无功功率可由公式所得，即

选取的目标函数为系统发电成本最低，数学模型为

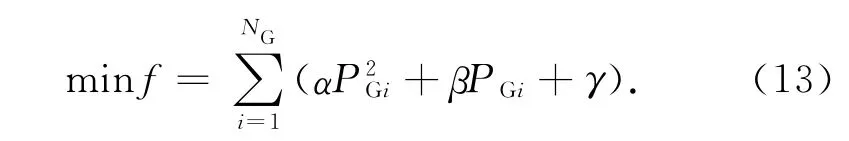
式中α，β，γ都是机组成本耗费曲线系数，；PGi是第i台发电机的有功出力.

2 动态调整罚函数

为将求解带约束的有功最优潮流问题转化为求解无约束优化问题，笔者结合了动态调整罚函数的策略.计算过程中可根据不等式约束在计算过程中的越界量大小动态地调节其罚函数，由此可实现转换.

在目标函数f（x，u）上附加一个越界不等式约束惩罚项，构成一个新的带惩罚性质的目标函数F（x，u），如：

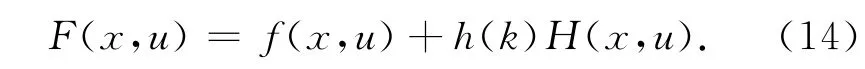
式中f（x，u）表示原目标函数；h（k）表示惩罚系数，k的数值随迭代次数的变化而变化.设迭代次数为k，则

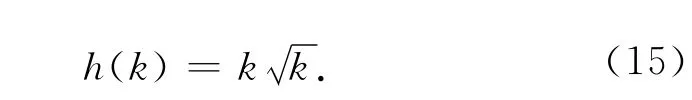
H（x，u）为惩罚项，其表达式为

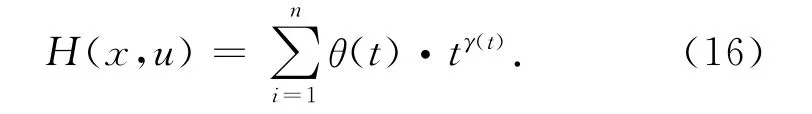
式中θ（t）表示惩罚系数；γ（t）表示惩罚力度.θ（t）与γ（t）的数值随不等式约束的越界量函数hi（x，u）的变化而调整.该文中有关罚函数的参数选择为

3 人工鱼群优化算法

3.1 基本人工鱼群算法简介

基本人工鱼群算法是根据在一片水域中，鱼都

式（19）、（20）中k＝1，2，…，n；xik，xjk和xinext分别代表状态向量Xi，Xj和人工鱼的下一步状态向量Xinext的第k个元素；Random（）表示［0，Step］间的随机数；Fc表示食物浓度值.

2）聚群行为.鱼的一种生存方式，大量或者少量鱼聚集成群进行集体觅食和躲避敌害.聚集时所应遵守准则为避免过分拥挤、与临近伙伴方向一致和尽可能靠近临近伙伴中心活动.设人工鱼当前状态为Xi，搜寻视野范围（dij≤Visual）内的伙伴数目nf，Kni为其形成集合及中心位置Xc，

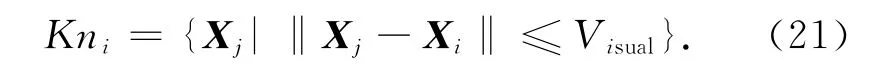
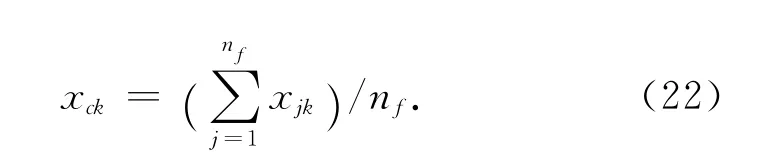
若Kni＝Φ，则说明在人工鱼视野范围内不存在其他伙伴，执行觅食行为；若Kni≠Φ，表明其视野范围内存在其他伙伴，即nf＞1，可按公式寻找伙伴中心位置，即能够自行或尾随其他鱼寻找到营养物质多的区域特点构造而成的.该算法是一种随机搜索优化算法，它从单条鱼的个体出发，通过模仿鱼群的觅食、聚群及追尾行为，在各个体的局部寻优过程中实现全局最优的目的［8-11］.

基本人工鱼群算法的工作过程分析：

1）觅食行为.设人工鱼的当前状态为Xi，在可见域内（di，j≤Visual）随机选择一个新状态Xj，若该新状态优于当前状态，则人工鱼往新状态方向前进一步，若该新状态不优于当前状态，则重新随机选择另一状态.若在经过一定尝试次数try＿number选择得不到比当前优异的状态，则随机选择一步移动.其数学表达式为

式中xck代表中心位置Xc的第k个元素；xjk代表第j（j＝1，2，…，nf）个伙伴Xj的第k个元素.该中心位置的食物浓度值用Fc表示，需满足

式中δ为拥挤度.该式说明伙伴中心食物浓度高且不太拥挤，可按照公式往前移动一步，否则执行觅食行为，即

3）追尾行为.鱼群中的一条或几条鱼发现食物时，其临近伙伴或远方伙伴都会尾随而来并随其快速到达食物点.

设人工鱼的当前状态为Xi，搜索其视野范围（di，j≤Visual）中食物浓度Fc为最大值的伙伴Xmax，若Fcmax＞δFci，说明该伙伴所处位置Xmax的食物浓度高、不拥挤，可按公式往前移动一步，反之则执行觅食行为，即

式中xmaxk代表状态向量Xmax的第k个元素.

4）公告板.人工鱼群算法设置了一个公告板，用来记录最优的人工鱼个体状态值及该人工鱼位置处的食物浓度值.每条人工鱼在行动一次后将自身的当前状态与公告板记录值进行比较，若优于该状态则替代公告板的状态.这样使在寻优过程中公告板总是保持最优结果.

3.2 算法的改进IAFSA

1）视野和步长的取值方法改进.

在基本人工鱼群算法当中，视野Visual和步长Step对算法的性能优劣起到关键作用.若采取固定的视野Visual值，在后期，算法容易陷入局部值且影响算法的收敛速度；取固定的步长Step值，算法后期在最优域内寻找局部最优值不利.因此，对人工鱼视野和步进作出自适应调整方法，即依据自身所处环境中食物浓度大小，自动调节其视野范围和前进步进大小，改进如下：

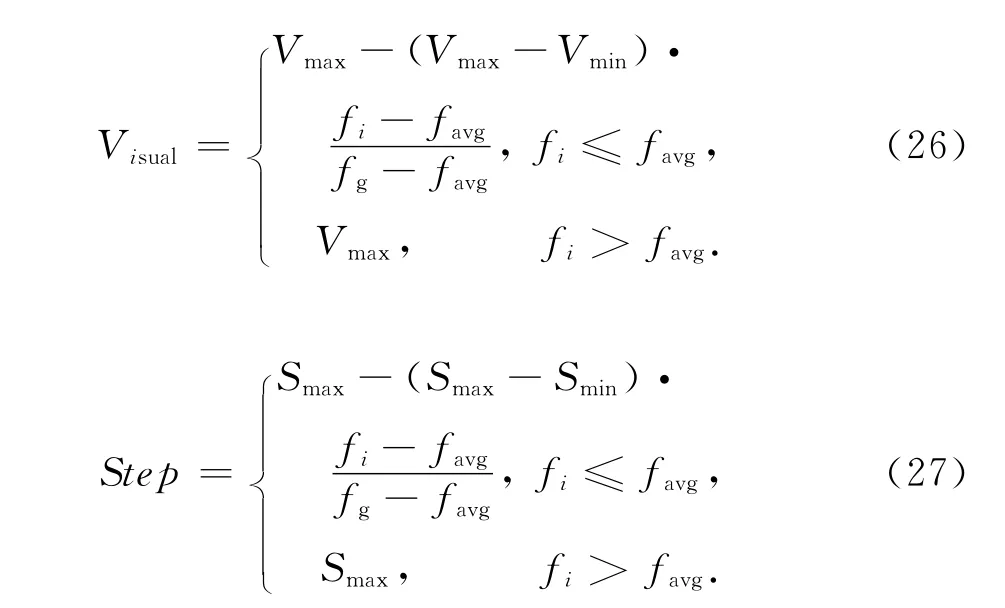
式中fi为当前个体Xi所处位置食物浓度值；fg为当代食物浓度最优值；favg为当代所有个体所处食物浓度平均值；Vmax为视野最大值，Vmin为视野最小值；Smax为步长最大值，Smin为步长最小值.

2）初始种群的改进.

初始鱼群的个体分布值直接影响到算法的全局收敛性.在基本鱼群算法中，由于其初始种群的产生具有随机分布性，若产生的初始解空间不能覆盖全局最优解，而鱼群所执行的搜索行为不能够在有限次数内寻找将覆盖空间扩展到全局最优解所在空间区域，则容易产生早熟行为.因此，对初始种群的产生，笔者采用均匀分布形式产生初始鱼群，即

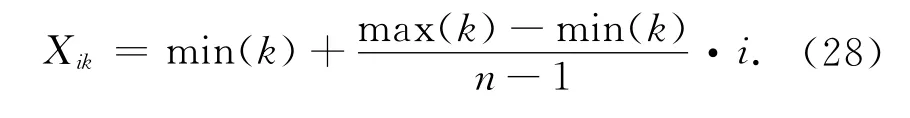
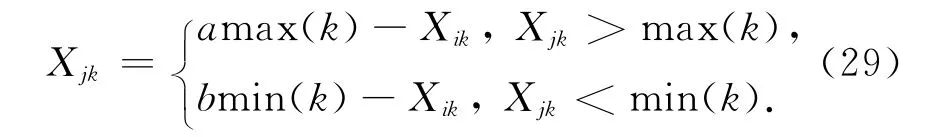
式中a，b为越界调整参数.

在觅食行为中，若执行了尝试移动次数try＿number后还是得不到比当前优异的解，则进行随机移动时，可按照公式进行，即

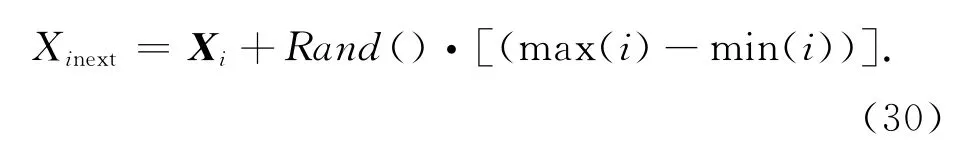
若按照式（25）中移动后所得到的最优值劣于移动，则停留在移动前的位置不变.该改进既能够保留最优个体、避免人工鱼退化，又可以提高收敛速度.

4）终止判据的改进.

在基本鱼群算法中，一般采用最大代数作为算法的停止准则.该方法简单易行，但是并不准确.因为可能在最大代数之前算法已经收敛，也可能在最大代数时算法还没有收敛.为了避免以上2种情况的发生，给定一最大代数范围和最小保留代数.若在鱼群进化过程中，到超过最小保留代数后，某一解仍为最优解，则停止进化.若在到达最大鱼群代数后，则将当前最优解输出，否则将继续搜索最优解.

3.3 基于IAFSA的OPF问题求解步骤

基于改进人工鱼群算法来求解最优问题，具体步骤：

1）输入原始数据.获得节点信息及各支路信息，设置人工鱼群算法参数：鱼群规模N，最大迭代

式中Xik表示第i（i＝1，2，…，n）条人工鱼的第k个分量；max（k）和 min（k）分别表示k的上、下限.

3）行动的改进.

在执行随机行为时，必须将游动到新的状态约束可行空间范围内.因此，若在随机游动到状态Xj在可行空间外，则可按公式进行越界限制，即次数Genmax，人工鱼群视野范围的上、下限Vmax，Vmin，人工鱼移动步长的上、下限Smax，Smin，拥挤度因子δ等.

2）设置当前迭代次数Gen＝0，初始种群的形成采取上述改进方法产生.

3）计算各人工鱼个体当前位置的食物浓度Fc，选取食物浓度值较小的进入公告板，保存其状态.

4）对各人工鱼个体视野范围内邻居数目Np进行计算，若Np＞0，分别执行追尾和聚群行为，对行动后食物浓度值Fc优异者为实际执行行为，否则选择觅食行为执行.

5）各人工鱼在执行每一次行动后，都先将自身状态与公告板的状态进行对比，取优异者重新进入公告板.

6）中止条件判断.判断是否满足设定的终止迭代准则，若满足则输出最优的计算结果，否则执行步骤5.

3.4 算法参数设置

算法应用matlab2009实现，其参数设置如下：

视野范围的上、下限分别为Vmax＝3.5，Vmin＝1.6，移动步长的上、下限分别为Smax＝1.0，Smin＝0.4；尝试次数try＿number＝6，拥挤度因子δ＝0.618.

4 实验验证与结果分析

应用笔者提出的改进方法，对标准的IEEE 57节点加入风电后的系统进行测试，其加入位置如图1所示（G表示发电机，WG表示风电场）.

为验证笔者提出的改进后算法的性能，对采用的相同节点系统，在相同初始条件下，通过30次计算并取平均值.采用基本人工鱼群算法（AFSA）和遗传算法（GA）进行对比计算.算例中3号机组配合风电运行，故没有计入费用.其发电费用结果比较如表1所示.

从表1中可以看出，3种算法各寻找到最优解中，IAFSA算法搜索到最优解，发电费用最低，表明IAFSA算法能够更好地获得全局解.

对于一个算法，其收敛速度也是一个重要判断性能指标.图2为改进人工鱼群、基本鱼群算法和遗传算法的收敛速度对比.

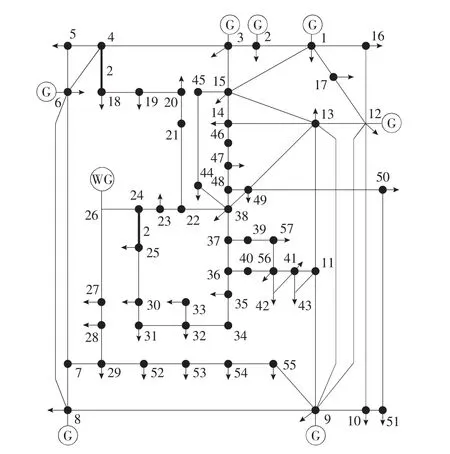
图1 加入风电场后的节点系统Figure 1 Node system diagram with wind farms

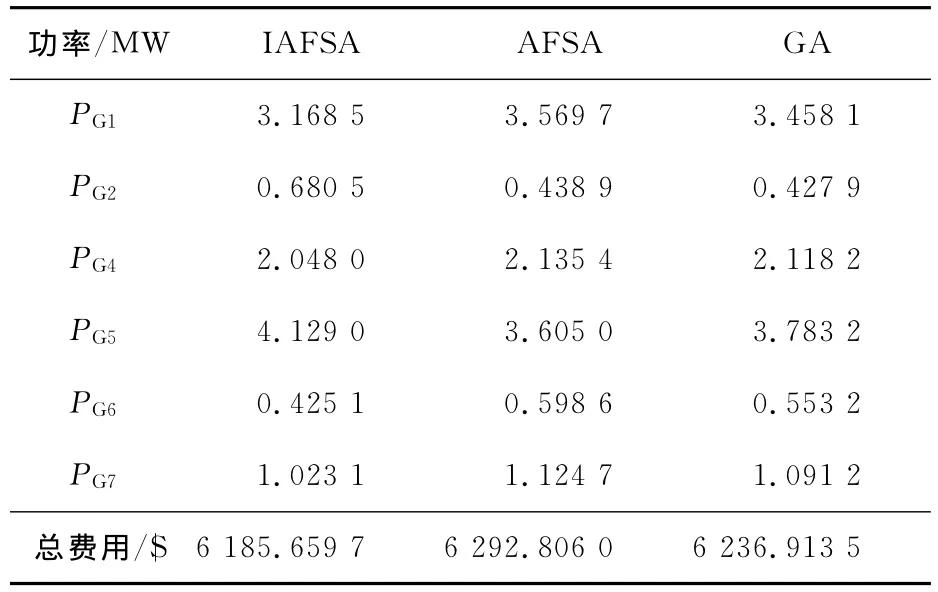
表1 寻优结果对比Table 1 Optimization results comparison

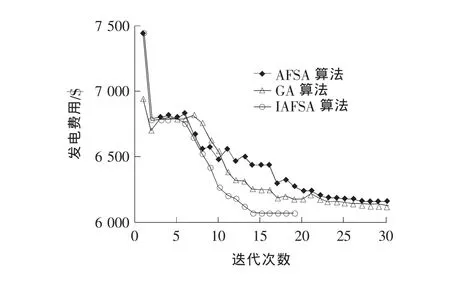
图2 算法收敛特性曲线Figure 2 Algorithm convergence characteristic curves

从图2收敛曲线可以看出，3种算法在收敛曲线的初始点和收敛特性在前3代基本相同，GA算法在第2次迭代当中找到最优解稍微由于IAFSA和AFSA算法.随着迭代次数的增加，IAFSA的爬坡率明显提高，并迅速找到最优解，在迭代过程中IAFSA的迭代次数明显少于AFSA算法和GA算法.结果证明了算法改进的有效性.

5 结语

笔者提出基于改进人工鱼群算法解决含风电场的最优潮流问题.改进后人工鱼个体的视野和步长能够根据自身所处环境自动地调整大小，增强了搜索全局解的能力和快速收敛的能力.对初始种群改进，促使生成初始鱼群在解空间内均匀分布，将初始鱼群扩延在最优解所在区域，以免后来的寻优过程中人工鱼聚集在局部解，避免了算法陷入局部；对行为改进既利于人工鱼个体跳出局部解，又能够保留了最优个体，避免退化，使人工鱼群算法智能性得到了加强.实验结果表明，改进后的人工鱼群算法步进保持了人工鱼群算法简单、易于实现的特点，而且能够提高算法的运行效率，增强了搜索全局最优解的能力和快速收敛能力.

［1］Larson A.Flicker emission of wind turbines caused by switching operations［J］.Power Engineering Review，IEEE，2002，22（2）：59.

［2］Tande J O G.Impact of wind turbines on voltage quality［C］.8th International Conference on Harmonics and Quality of Power，Athens，Greece，1998.

［3］Pazderin A，Yuferev S.Power flow calculation by combination of Newton-Raphson method and Newton's method in optimization［C］.35th Annual Conference of IEEE Industrial Electronics，Porto，The Portuguese Republic，2009.

［4］孙英云，何光宇，梅生伟.基于Filter集合的内点最优潮流新算法［J］.电工电能新技术，2007，26（2）：29-33，53.

SUN Ying-yun，HE Guang-yu，MEI Sheng-wei.A new optimal power flow algorithm based on filter interior point method［J］.Advanced Technology of Electrical Engineering and Energy，2007，26（2）：29-33，53.

［5］Moasheri S R，Khazraei M.Optimal power flow based on modified genetic algorithm［C］.Power and Energy Engineering Conference（APPEEC），Asia-Pacific，2011.

［6］俞俊霞，赵波.基于改进粒子群优化算法的最优潮流计算［J］.电力系统及其自动化学报，2005，17（4）：83-88.

YU Jun-xia，ZHAO Bo.Improved particle swam optimization algorithm for optimal power flow problems［J］.Proceedings of The Electric Power System and Automation，2005，17（4）：83-88.

［7］刘盛松，侯志俭，蒋传文.基于混沌优化与线性内点法的最优潮流算法［J］.电网技术，2003，27（9）：23-28.

LIU Sheng-song，HOU Zhi-jian，JIANG Chuan-wen.Optimal power flow algorithm based on chaos optimization and linear interior point method［J］.Power System Technology，2003，27（9）：23-28.

［8］李晓磊.一种新型的智能优化方法——人工鱼群算法［D］.杭州：浙江大学，2003.

［9］陈爱军，刘爱国.基于人工鱼群算法的静态电压稳定评估［J］.电网与清洁能源，2010，26（10）：35-38.

CHEN Ai-jun，LIU Ai-guo.Static voltage stability assessment based on artificial fish-swarm algorithm［J］.Power System and Clean Energy，2010，26（10）：35-38.

［10］孙浩.基于改进人工鱼群算法的可用输电能力研究［D］.吉林：东北电力大学，2008.

［11］刘健.人工鱼群算法在电网网架规划中的应用研究［D］.秦皇岛：燕山大学，2007.