改进的合成孔径雷达旁瓣抑制空间变迹算法

杨 科 廖桂生 徐 青 王伟伟

(西安电子科技大学雷达信号处理国家重点实验室，陕西 西安 710071)

引 言

合成孔径雷达(SAR)具有成像分辨率高、穿透能力强、全天候工作等优点，能够满足地表成像、地面目标检测等应用需求[1-2]。由于SAR图像中含有强散射点目标，这些点目标的高旁瓣会完全湮没邻近弱目标，进而影响后续的SAR图像的特征识别以及目标检测，因而旁瓣抑制显得尤为重要。频域加窗处理是最为常用的旁瓣抑制方法，这种方法能有效抑制旁瓣，但是它会展宽主瓣，降低图像分辨率。切趾滤波技术能够较好地保持主瓣分辨率，但是它需要事先找到一种特殊的图像域滤波函数，并且通过迭代来实现旁瓣抑制[3]。压缩感知技术是一种基于稀疏约束的欠定方程求解技术，它能够抑制旁瓣和噪声，并且可以实现超分辨成像，但是该技术不适用于目标散射系数非稀疏的SAR场景[4-5]。

空间变迹(SVA)算法是Stankwitz等人提出的一种有效的旁瓣抑制算法，它在不损失分辨率的前提下能够有效地抑制旁瓣[6-7]。经过多年发展，SVA算法被广泛应用到超分辨技术、斜视SAR、超宽带SAR等领域[8-12]。但SVA算法仅适用于整数倍带宽采样的SAR数据，对于非整数倍采样的SAR数据，众多学者相继提出了两大类改进SVA算法，第一类改进算法采用三点滤波器对SAR数据进行旁瓣抑制，该类算法主要包括通用空间变迹(GSVA)算法[14]和改进通用空间变迹(MGSVA)算法[12,15]，GSVA算法能够抑制一部分旁瓣，但还会留有较多的剩余旁瓣，MGSVA算法提出了剩余相位差的概念，能够较好地抑制主瓣附近的剩余旁瓣，但是在剩余相位差为较大值的情况下，该算法会损失部分主瓣能量。第二类改进算法采用五点滤波器，该类算法是一个约束优化问题[10]，导致该类算法的运算量极大，文献[13]提出的鲁棒空间变迹(RSVA)算法将优化问题转化为二维约束空间多个顶点的极值问题，但相应的计算量仍然很大。相对于第二类算法，第一类算法的优化空间为一维空间，只需计算两个顶点的最优权系数，因此不会占用太大运算量。

针对现有的改进SVA算法的不足，提出一种基于三点滤波器的改进SVA算法，由于非整数倍带宽采样导致理想脉冲响应函数(IPR)具有复杂的离散域表达形式，使得相应的SAR旁瓣抑制不易实现，因此构建了一个新的近似脉冲响应函数，使其既能保留理想脉冲响应函数的部分特性，又能较好地抑制高幅值旁瓣，同时根据构建的脉冲响应函数得到新的频域窗函数，并根据旁瓣抑制要求给出新的约束条件。该算法在保持主瓣能量的前提下能够快速有效地抑制旁瓣，仿真实验和实测数据处理验证了该算法的有效性。

1 理论分析

1.1 现有的改进SVA算法

SVA算法及改进SVA算法是一种非线性自适应加权算法，采用一组升余弦类频域加权窗函数W(f)，对有限带宽SAR数据G(f)进行加权处理。分析重点是一维数据的处理情况，对于二维数据处理有多种实现方式[7,12,16]，分别对距离向和方位向进行一维处理[12]即为一种较为常用的方式，在后续仿真和实测数据处理中会采用这一方式。

考虑一个通用对称的2n+1有限冲击响应滤波器，其在频域上的加权窗函数W(f)表达式为

(1)

式中：a是归一化参数；αi是窗函数的权系数；fs是采样率；f的取值范围为[-f0/2,f0/2]，f0是SAR数据的信号带宽。式(1)在离散域上的脉冲响应函数为

(2)

式中ws=f0/fs.根据式(2)和升余弦类窗函数的物理特性，可以确定a和αi的取值范围。

改进SVA算法是分别对SAR数据的实部和虚部进行旁瓣抑制，以下给出改进SVA算法的旁瓣抑制流程图。

图1 改进SVA算法旁瓣抑制流程图

第一类改进算法采用三点滤波器，相应的参数为a、α1，在一维空间V(α1)的优化问题简化为两个顶点的极值问题，计算α1取最小值和最大值的加权数据，然后判定两者在各个位置点m处的符号，若符号相反则该点的输出为0，否则选取较低幅值作为输出[7,14]。第二类改进算法采用五点滤波器，即n=2，因此相应的参数为a、α1、α2.根据式(2)及归一化增益要求，可以认为a是α1和α2的函数[10]，最优空间是二维空间V(α1,α2)，因此该类算法的运算量比较大。

1.2 基于IPR分析的改进SVA算法

对于整数倍带宽采样的SAR数据来说，频域加权窗函数W(f)具有如下形式[14]

W(f)=1+2αcos(2πf/f0) 0≤α≤1/2

(3)

式中：α是窗函数的权系数；f的取值范围为[-f0/2,f0/2].该窗函数在连续域上的脉冲响应函数为

I(x)= sin c(f0x)+α{sin c[f0(x-1/f0)]+

sin c[f0(x+1/f0)]}

(4)

当采样率是整数倍带宽时，即fs=Mf0(M为正整数)，采样间隔Δx=1/fs；x=mΔx；1/f0=MΔx,式(4)的离散表达式为

I(m)= sin c(wsm)+α{sin c[ws(m-M)]+

sin c[ws(m+M)]}

(5)

当采样率不是整数倍带宽时，即fs=Rf0(R为正实数)，采样间隔Δx=1/fs;x=mΔx;1/f0=RΔx，式(4)的离散表达式为

I(m)= sin c(wsm)+α{sin c[ws(m-R)]+

sin c[ws(m+R)]}

(6)

在式(6)中，由于R值不是正整数，不存在sin c[ws(m-R)]、sin c[ws(m+R)]离散值。对比式(2)和式(6)可以发现：为了获得式(6)较为精确的离散值，可以通过式(2)多点求和的方法对该值进行拟合。但是如果拟合点数n取值较大时，将会大大增加运算复杂度，现有的改进SVA算法一般将n取值为1或2.根据前面的分析可知：基于五点滤波器的改进SVA算法是个最优化问题，这会大大增加运算量，为此针对现有的基于三点滤波器SVA算法的不足之处，提出一种新的基于三点滤波器的改进SVA算法。

为了最大程度拟合式(6)的离散值，选取最靠近R的正整数MR，将sin c[ws(m-R)]、sin c[ws(m+R)]用sin c[ws(m-MR)]、sin c[ws(m+MR)]代替，式(6)变换为

I(m)= sin c(wsm)+

α1(m,R)sin c[ws(m-MR)]+

α2(m,R)sin c[ws(m+MR)]

(7)

(8)

(9)

由式(7)可知：经过变换后的脉冲响应函数保持了三点滤波器这一最简单形式，但是权系数α1(m,R)、α2(m,R)变成了m的函数，即一维优化空间V(·)随m值的变化而变化，这会导致SVA算法非常复杂，甚至导致SVA算法不可行。事实上对于SAR图像来说，只有主瓣附近的少数旁瓣有较高幅度，SAR旁瓣抑制应该重点考虑这些旁瓣，为此可以构建一个形式简单的脉冲响应函数来近似代替式(7)，并且通过设定新构建的脉冲响应函数在特定点为理想值，使其既能保留式(7)的部分特性又能较好地抑制高幅值旁瓣。关于这一特定点具体位置的选取，在下文设置约束条件时给出。

在式(8)和式(9)中，包含因子π[(MR-R)/R]，这一因子即是MGSVA算法中的剩余相位差p，在构建新的脉冲响应函数时需要考虑这一因子。根据以上的分析，构建新的近似脉冲响应函数为

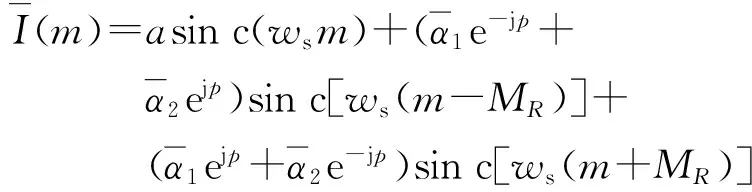
(10)

(11)

式中， Λs=(R/MR)f0.

为了保证窗函数有效，引入约束条件式(12)～(14)，其中函数对称性要求式(12)成立，归一化增益要求式(13)成立。为了抑制主瓣附近的高幅值旁瓣，要求式(14)成立，即式(10)新构建的脉冲响应函数在特定位置点M0上的大小被强制赋予理想值I(M0)，这一理想值可以通过式(7)～(9)得到。

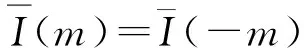
(12)

(13)

(14)

根据约束条件式(12)～(14)可得

(16)

(17)

为了实现旁瓣抑制，在权系数分别取最大、最小值的两种情况下，相应的脉冲响应函数具有不同符号，可以通过以下符号比较最终判定M0的大小

(18)

(19)

选取M0为M1，利用式(15)～(17)计算式(10)在m=M1+1位置的脉冲响应函数值，如果公式(18)成立，则M0=M1，否则M0=M2.通过选取M0为M2，并判断式(19)是否成立，也可以得到相同的结果。

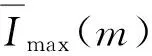
(a) M0=M1

(b) M0=M2图2 脉冲响应函数波形图

整个旁瓣抑制过程如下：

1) 选取M0为M1，α为1/2，通过式(7)～(9)计算脉冲响应函数在M0点的理想值I(M0)；

5) 判定g′(m)和g(m)在各个位置点m的符号，若符号相反则该点的输出为0，否则选取较低幅值作为输出。

2 实验结果分析

2.1 性能分析

2.1.1 主要影响因素

本文算法权系数如式(15)～(17)所示，分别包含影响因素R、MR、p以及M0，具有如下关系为

(20)

由式(20)可知：MR、p均由R所决定，因此，可以认为本文算法权系数的主要影响因素为R和M0.

R和采样率fs、信号带宽f0具有如下关系为

R=fs/f0=f3(fs,f0)

(21)

单纯从式(21)看：不同的采样率以及信号带宽均会影响到本文算法的旁瓣抑制效果。

实际中，由于引入影响因素M0，通过保证条件式(14)成立，使得构建的脉冲响应函数赋予理想值I(M0)，可以有效降低不同的采样率以及信号带宽对旁瓣抑制效果的影响。图3以积分副瓣比为指标，给出不同R值所对应的旁瓣抑制效果，由图可知，M0的存在起到了一个较好的调节约束作用，从而保证不同R值所对应的积分副瓣比趋于一致。旁瓣抑制实际效果如图4所示，其中R分别取1.9、2.7.由以上分析可知：本文算法受影响因素R的影响较小，具有较好的旁瓣抑制效果。

图3 不同R 值的积分副瓣比

(a) R=1.9

(b) R=2.7图4 不同R值本文算法旁瓣抑制效果

2.1.2 权系数形式

权系数形式不同，旁瓣抑制效果也不同。在第一类算法中，GSVA算法引入归一化权系数a，并通过频域窗函数的物理特性来约束权系数的变化范围，如图5(b)所示，该算法会留有部分剩余旁瓣。MGSVA算法引入剩余相位差p的概念，对GSVA算法的权系数进行修正，如图5(c)所示，该算法能够有效抑制主瓣附近的旁瓣。在p≪1的情况下，MGSVA算法可以忽略p对主瓣幅度的影响[12]，但是在实际情况中(例如R=1.7，则p=0.55)，以上条件不再成立。如图6所示，当p不可忽略时MGSVA算法会损失部分主瓣能量。本文算法没有对p的范围进行约束，不会降低主瓣幅度，同时通过约束条件式(14)，使得本文算法的权系数保留理想脉冲响应函数的部分特性。如图5(d)和图6所示，采用本文的权系数既能保持主瓣能量，又能有效抑制主瓣附近的旁瓣。

(a) 旁瓣抑制前数据

(b) GSVA算法

(c) MGSVA算法

(d) 本文算法图5 各种算法旁瓣抑制效果比较

图6 距离向剖面图比较

2.1.3 运算量分析

第一类算法和第二类算法均能有效抑制SAR图像中的高旁瓣，但是相对于第一类算法，第二类算法的不足之处是运算复杂、计算量大。图7对RSVA算法和本文算法的运算量进行比较，图中横坐标表示SAR图像数据的大小，二维SAR数据的某一维保持128个采样点不变，另一维从128线性变化到1 024个采样点，如图7横坐标所示。为了降低运算量，已将RSVA算法的优化问题转化为二维约束空间多个顶点的极值问题，由图可知，RSVA算法仍要消耗较大运算量(仿真环境：Intel(R) Core(TM)2 Duo CPU E4500 @ 2.20 GHz).

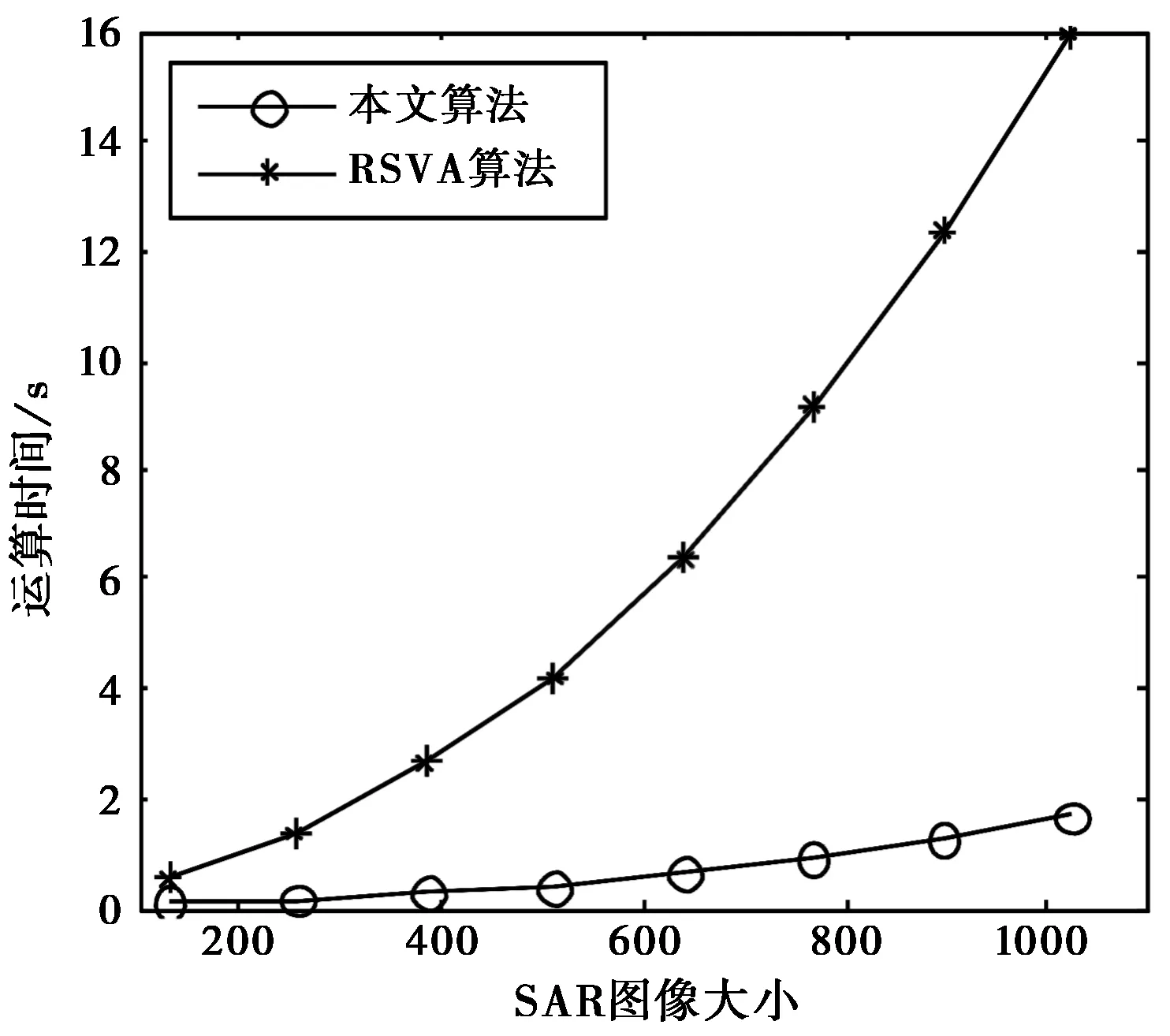
图7 运算时间比较

2.2 实测数据处理结果

图8是对加拿大RADARSAT1实测数据的处理结果，图8(a)是旁瓣抑制前的SAR数据，由于未进行旁瓣抑制，可以明显地发现强散射点目标具有较高的旁瓣。图8(b)是GSVA算法的旁瓣抑制结果，由图可知，右上角强散射点目标在距离向上仍保留部分剩余旁瓣。图8(c)是MGSVA算法的旁瓣抑制结果，该算法能较好地抑制旁瓣，但是幅度由27.6 dB降至24.6 dB，即该算法会损失散射点目标部分能量。由图8(d)可知：本文算法既能较好地抑制旁瓣，又能保持散射点目标的能量。

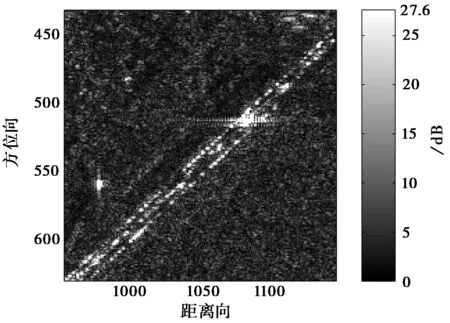
(a) 旁瓣抑制前数据

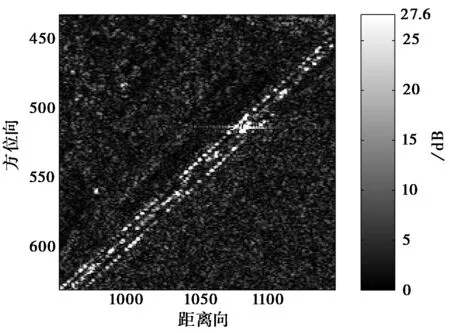
(b) GSVA算法

(c) MGSVA算法

(d) 本文算法图8 各种算法实测数据旁瓣抑制效果

3 结 论

SAR图像中的强散射点目标的高旁瓣会极大影响邻近点目标图像的后续处理，SVA算法及改进SVA算法是一种有效的旁瓣抑制算法，但是现有的改进SVA算法存在运算量大、剩余较多旁瓣或损失主瓣能量等问题。针对以上这些问题，提出新的改进SVA算法，该算法构建了新的离散域近似脉冲响应函数，改进了频域窗函数形式，给出了新的约束条件，根据约束条件可以得到一组权系数，利用这些权系数实现SAR数据加权，最后通过比较最大加权SAR数据和最小加权SAR数据来实现旁瓣抑制。该算法在保持主瓣能量的前提下能够快速有效地抑制旁瓣，仿真实验和实测数据处理验证了该算法的有效性。

[1] 张 云, 姜义成, 李宏博. 一种改善SAR对舰船目标成像质量的新方法研究[J]. 电波科学学报, 2009, 24(4): 588-592.

ZHANG Yun, JIANG Yicheng, LI Hongbo. Improving synthetic aperture radar imaging of ship targets[J]. Chinese Journal of Radio Science, 2009, 24(4): 588-592. (in Chinese)

[2] 杨 文, 陈嘉宇, 孙 洪, 等. 基于SAR图像的点状目标检测方法研究[J]. 电波科学学报, 2004, 19(3): 362-366.

YANG Wen, CHEN Jiayu, SUN Hong, et al. Study on point targets detection in SAR images [J]. Chinese Journal of Radio Science, 2004, 19(3): 362-366. (in Chinese)

[3] 张先义, 苏卫民, 史 记, 等. 切趾滤波旁瓣抑制技术在合成孔径雷达中的应用[J]. 电子与信息学报, 2008, 30(4): 902-905.

ZHANG Xianyi, SU Weimin, SHI Ji, et al. Application of apodization filtering sidelobe suppression technique to synthetic aperture radar[J]. Journal of Electronics & Information Technology, 2008, 30(4): 902-905. (in Chinese)

[4] 寇 波, 江 海, 刘 磊, 等. 基于压缩感知的SAR抑制旁瓣技术研究[J]. 电子与信息学报, 2010, 32(12): 3022-3026.

KOU Bo, JIANG Hai, LIU Lei, et al. Study of SAR sidelobe suppression based on compressed sensing[J]. Journal of Electronics & Information Technology, 2010, 32(12): 3022-3026. (in Chinese)

[5] 朱 丰, 张 群, 顾福飞, 等. 合成孔径雷达运动目标谱图二维压缩与重构方法[J]. 电波科学学报, 2012, 27(1): 157-164.

ZHU Feng, ZHANG Qun, GU Fufei, et al. Two dimensional SAR moving target spectrogram compressing and reconstructing method[J]. Chinese Journal of Radio Science, 2012, 27(1): 157-164. (in Chinese)

[6] STANKWITZ H C, DALLAIRE R J, FIENUP J R. Spatially variant apodization for sidelobe control in SAR imagery[C]//Record of the 1994 IEEE National Radar Conference. Atlanta, GA, USA, 1994: 132-137.

[7] STANKWITZ H C, DALLAIRE R J, FIENUP J R. Nonlinear apodization for sidelobe control in SAR imagery[J]. IEEE Transactions on Aerospace and Electronic Systems, 1995, 31(1): 267-279.

[8] PANIGRAHI R K, MISHRA A K. A novel algorithm for apodization and super-resolution in fourier imaging[C]//2011 International Conference on Devices and Communications (ICDeCom). Mesra, India, 2011: 1-5.

[9] NI Chong, WANG Yanfei, XU Xianghui, et al. A super-resolution algorithm for synthetic aperture radar based on modified spatially variant apodization[J]. Science China (Physics Mechanics & Astronomy), 2011, 54(2): 355-364.

[10]NI Chong, WANG Yanfei, XU Xianghui, et al. A SAR sidelobe suppression algorithm based on modified spatially variant apodization[J]. Science China (Technological Sciences), 2010, 53(9): 2542-2551.

[11]CARLOS C R, ROMANO S L, MATEO B G. Spatially variant apodization for squinted synthetic aperture radar images[J]. IEEE Transactions on Image Processing, 2007, 16(8): 2023-2027.

[12]XU Xiaojian, NARAYANAN R M. Enhanced resolution in SAR/ISAR imaging using iterative sidelobe apodization[J]. IEEE Transactions on Image Processing, 2005, 14(4): 537-547.

[13]CARLOS C R, ROMANO S L, MATEO B G. Robust SVA method for every sampling rate condition[J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(2): 571-580.

[14]SMITH B H. Generalization of spatially variant apodization to noninteger Nyquist sampling rates[J]. IEEE Transactions on Image Processing, 2000, 9(6): 1088-1093.

[15]XU Xiaojian, NARAYANAN R M. SAR image enhancement using noninteger Nyquist SVA technique[C]//IEEE Antennas and Propagation Society International Symposium. San Antonio, Texas, USA, 2002, 4: 298-301.

[16]LEE J A C, MUNSON D C J. Spatially variant apodization for image reconstruction from partial Fourier data[J]. IEEE Transactions on Image Processing, 2000, 9(11): 1914-1925.