基于数学形态学和瞬时无功功率分解的电能质量扰动参数估计
王丽霞
(中铁第一勘察设计院集团有限公司,陕西 西安 710043)
1 引言
电网中各种非线性负载的大量应用,导致电能质量急剧下降[1],而治理电能质量,需要先判断所发生的电能扰动的类型,才能进一步分析其形成原因,进而采取相应的措施进行补偿和改善。IEEE通过扰动参数明确定义了各种电能扰动[2],若能获取扰动参数,就可准确的对扰动类型进行判断。同时,近年来国家智能电网的发展,提出现代电网应能够按照用户要求提供不同质量的电能。而如何评估电能质量的高低,也需获得电能质量扰动的相关参数[3]。因此,电能质量扰动参数的获取具有非常重要的意义。
电能质量扰动分为稳态扰动和暂态扰动,稳态扰动的参数可通过统计能数学手段较为容易的获得,而暂态电能质量扰动因为发生的时间短,特征复杂,所以参数较难获取。由于暂态电能质量扰动信号是一种典型的非平稳信号,因此可以通过信号处理方法来进行获取。信号处理的方法有很多,包括基于时域,基于频域和基于变化域的方法[4]。其中有很多方法以应用在电能质量扰动检测和分类相关领域上,被证明其分析结果能够反映信号的特征[5-7],是行之有效的,但是用于参数估计,还存在着一些问题。如傅里叶变换计算简单,可以很好的反映信号的频率特征,但缺乏时间分辨率,难以反映暂态扰动信号的时域信息;小波变换通过分解能够获得信号的时间-频带信息,在暂态扰动的检测上表现优异,被称为信号的放大镜,但是用于参数测定,难以建立小波系数和扰动参数的联系;S变换、双线性时频分布等时频分布方法,能够全面的反映信号的时间频率联合特征,但也存在着计算量大、冗余信息多、特征参数提取困难等问题,同时大量积分运算不仅耗时,而且也会因运算步骤过多而导致计算误差增大。
IEEE是从时域上定义扰动的,因此从时域上提取扰动特征具有一定的优势。本文采用了两种基于时域的信号处理方法,瞬时无功功率理论和数学形态理论,对几种常见的电能质量扰动信号进行分析计算,获得其相关参数,仿真结果表明,该方法是有效的。
2 瞬时无功功率分解和数学形态学
2.1 瞬时无功功率分解理论[8]
瞬时无功功率分解理论指出将三相系统电压经过αβ变换和dq变换可将基频分量转换为直流分量,而其他分量仍为交流分量,采用直流滤波器,即可获得信号的基波成分。这些基波成分中包含了幅值变化的信息。计算公式如下所示:

分析单相信号时,可通过虚构分量来进行计算。假设 uα=Acos(ωt+ψ),计算公式(1)可得:

则uα可用uα乘以一个常数来构造,uβ可通过将uα平移滞后1/4个周期来构造。若要恢复信号,可通过反变换实现。
2.2 数学形态学滤波理论
数学形态学[9]是近年来提出的一种从图像处理演变而来的新方法,它利用图像处理理论提取信号的主要特征,而不改变其大体形状,可应用于滤波和边缘检测等领域。这种基于时域的非线性数学方法具有计算简单、实时性强的特点,有较好的应用前景。文献[10]指出,在直流阶跃的信号消噪上,形态滤波的效果甚至更优于小波分析,但计算量要小得多。因此,本文构造了基于数学形态学得广义形态滤波器作为直流滤波器,构造方法如下所示。
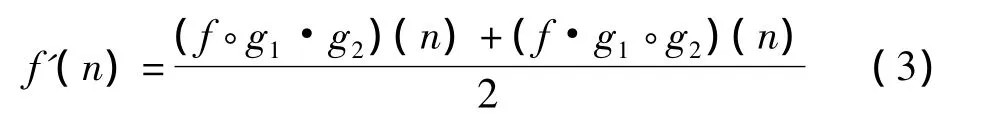
f代表待处理的信号,·和·分别代表形态开运算和闭运算;g1和g2代表形态结构元素。g1和g2的长度和形状影响滤波的效果,在本文中,g1为1/4周期长度的扁平结构元素,g2为比g1长度多一个采样点的扁平元素,用以去除的ud和uq分量中的谐波和噪声成分。
3 算法设计
电能质量扰动的种类有很多,根据不同的特点可将常见的电能质量扰动分为三类:一类是基波幅值变化类,长期的有过电压,欠电压和中断等,短时的有电压暂升,电压暂降和凹陷;第二类是包含其他频率成分的加性扰动,包括最常见的谐波,暂态振荡等;第三类则是两者的复合形式,如电压暂降时有时会伴有振荡现象,或是谐波引起的电压暂降等。长期的扰动参数测量相对容易,理论也较为成熟,加性扰动成分可以通过傅里叶变换进行分析。因此本文着重研究一些常见的暂态电能质量扰动的参数测定方法,其中最主要的就是最常见的电压暂降扰动。首先说明参数测定的过程,如图1所示。

图1 幅值特征获取流程图
选取经过滤波的ud和uq分量进计算信号的特征,计算公式和流程如下式所示:

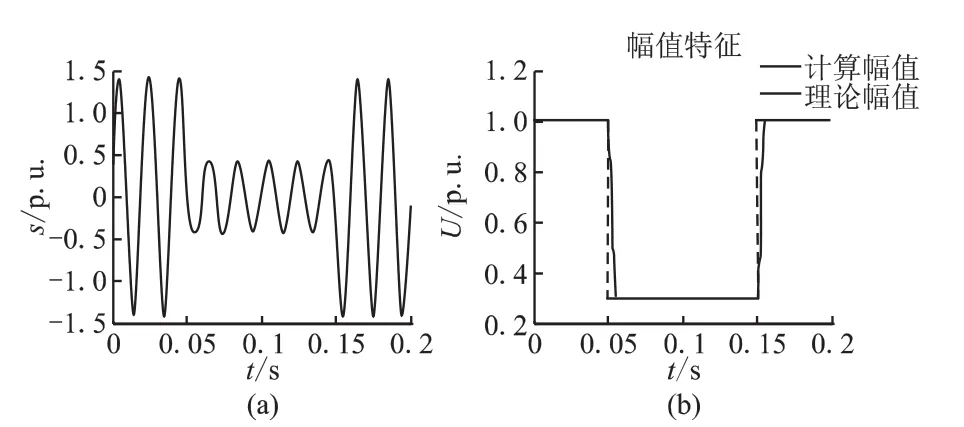
图2 电压暂降及其幅值特征
图2(a)为预设电压暂降信号,采样率为5000Hz,(b)为扰动信号的幅值特征,其中实线表示根据上述方法计算所提取到的幅值,虚线表示预设幅值变化曲线。由图可知,所提取获得的幅值基本于预设是吻合的,在突变点附近,有一段过渡过程,产生的原因是因为,在虚构αβ采用了平移的构造方法,导致两分量幅值突变的时间点不同。但是,因为构造平移的均为1/4周期,因此此过渡段也是有规律可循的。在本例中,扰动信号从第0.05s时发生暂降,0.15s时结束,计算所得的幅值从第0.05s开始逐渐下降,1/4个周期后降为0.3p.u.,0.15s时开始恢复,1/4个周期恢复为1p.u.。
由以上分析可知,提取到的电压信号中包含了暂降的幅值变化幅度和时间信息,根据IEEE的定义,电压暂降参数包括扰动的幅值A(0.1p.u.<A<0·9 p.u.),扰动持续时间t(T/2<t<1min)。对U进行进一步计算,获得以上参数。令:
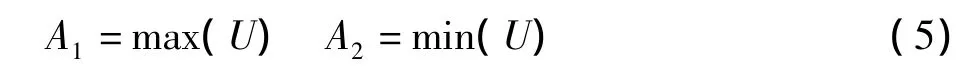
max()和min()返回数组的最大和最小值,即该扰动信号的最大幅值和最小幅值,然后判断A1和A2值所处范围:
若两者均处在[0.9,1.1]的范围内,则没有发生暂变扰动;
病梢被害后,节间缩短,发出的叶片细长,质脆而硬,长势细弱,生长缓慢,病部表层覆盖一层白粉。受害严重时,病梢部位变褐枯死。初夏以后,白粉层脱落,病梢表面显出银灰色。
若A1>1.1,则发生了电压暂升,A1即为暂升的幅值;若A2<0.9,则发生了电压暂降,A2即为暂降的幅值;若A2<0.1,则发生了电压凹陷,A2即为凹陷的幅值;
另外一个重要的扰动时间为扰动持续时间,若获得扰动起止时刻,则可以获得准确的扰动时间。在本算法中,将幅值开始变化的时刻作为扰动的起时刻t1,将幅值开始恢复时刻作为扰动终止时刻t2。为了提取这两个边沿时刻,采用数学形态学Top-hat运算(高帽变换)[9],计算公式如下所示:

其中g为结构元素,本算法中选取长度为5点的扁平结构元素。

图3 幅值特征及其高帽变换
根据以上算法,得到幅值特征的TOP-hat变换,即图3所示的定位脉冲,检测定位脉冲的起点(非零值)作为扰动起(止)时刻,由此获得四个参数分别为:

表1 电压暂降及其扰动参数
4 仿真分析
电压暂升、暂降和凹陷,均属于电压幅值变化类扰动,三者的测定过程相似。

表2 暂态扰动及其扰动参数

图4 定位脉冲及其阈值处理
当电力系统中存在的噪声较大时,考虑噪声的影响,对第二节中电压暂降扰动添加信噪比为40dB的高斯白噪声,获得的电压暂降定位脉冲如图4所示。由图可知,由于受噪声的影响,所提取到的定位脉冲存在着一些噪声引起的微小波动,也会表现为奇异点,为克服此问题,对定位脉冲进行阈值处理,然后检测扰动起止时刻。阈值处理的算法如下:

40dB白噪声存在的情况下获得的仿真结果如下所示。

表3 暂态扰动及其扰动参数(含噪声)
由仿真结果可知,在存在噪声时获得的暂变参数有一定误差,参数A误差小于1p.u.,扰动时间小于1ms。
除了上述扰动,还存在一些常见的电能质量扰动如谐波,暂态振荡以及复合类扰动。在上述过程中已获得了幅值变化类扰动的相关参数,则可以通过这些参数反向获得准确的基波成分,将其与原扰动信号相减,即可获得加性的扰动成分,对加性扰动成分做简单的傅里叶变换和过零点数检测,就可获得加性扰动的频率成分和扰动时间。
5 结论
(1)本文所提出的采用瞬时无功功率分解理论及广义形态滤波,数学形态学高帽变换进行参数测定的方法,对电压暂降,电压暂升和电压凹陷的参数测定是行之有效别的;
(2)在噪声存在的情况下,该方法存在一定的误差,但误差较小;
(3)利用该方法可以反构获得扰动信号的基波成分,进而获得加性扰动成分,为加性扰动参数的获得打下基础;
(4)如何对更多类型的电能质量扰动信号进行参数测定,并进一步提高在强噪环境下的准确率,是进一步进行的工作。
[1]徐永海,肖湘宁.电力市场环境下的电能质量问题[J].电网技术,2004,28(22):48 -52.
[2]林海雪.现代电能质量的基本问题[J].电网技术,2001,25(10)5-10.
[3]陈磊,许永海.浅谈电能质量评估的方法[J].电气应用,2005,24(1):58-65.
[4]张斌,刘晓川,许之晗.基于变换的电能质量分析方法[J].电网技术,2001,25(1):25 -29.
[5]赵凤展,杨仁刚.时频分析方法在电能质量扰动检测与识别中的应用[J].华北电力大学学报,2006,33(5):33 -37.
[6]任震,石志强.小波分析及其在电力系统中的应用:(三)工程应用技术[J].电力系统自动化,1997,12(3):9 -12.
[7]Ren Zhen,Shi Zhiqiang.Wavelet Analysis and it’s application in power systems:(3)Engineering Applications[J].Automation of Electric Power Systems,1997,12(3):9 -12.
[8]曾纪勇,丁洪发,段献忠.基于数学形态学的谐波检测与电能质量扰动定位方法[J].中国电机工程学报,2005,25(21):57 -61.
[9]崔屹.图象处理与分析―数学形态学方法及应用[M].北京:科学出版社,2002.
[10]王丽霞,何正友,赵静,等.小波变换和数学形态学在电力扰动信号消噪中的应用[J].电力系统保护与控制,2008(36):30-35.

