能量平衡原理在大型龙门加工中心动横梁结构优化中的应用*

王 宇，朱金波，阳 红，陈 强，殷国富

(1.四川大学制造科学与工程学院，成都 610065;2.四川迪泰机械有限公司，四川 德阳 618000)

0 引言

大型龙门加工中心是机械制造加工的一种重要设备，作为加工大型、重型零件的主要机床，在航空航天、汽车制造、船舶工业、能源等领域扮演着举足轻重的角色。动横梁作为龙门加工中心连接机床主轴和立柱的关键部件，其结构和动、静态特性的优劣直接影响龙门加工中心的整体性能。传统的横梁结构设计基于一种长期积淀下来的经验设计方法，虽然根据结构计算分析能够初步判断横梁的性能缺陷，但是在结构改进方面没有更为合理的依据，对改进结构也没有科学的评价方法。

我国学者在横梁结构优化方面都有较为深刻的研究，致力于从不同的角度提出结构优化的理论与方法。大连理工的王晓煜对龙门加工中心横梁部件的纵、横截面的筋肋分布形式进行拓扑优化［1］。大连华根机械的兰铁军依托ANSYS软件分别对横梁进行了结构拓扑优化和力学性能验证，实现横梁的轻量化设计［2］。沈阳理工的杜钟魁对横梁进行模态和谐响应分析，得出横梁在受外部激振力下的动态响应特性，为横梁的优化设计提供了理论依据［3］。

上述文献主要在横梁的静力学分析和拓扑优化的基础上进行结构的改进，或者通过模态分析找出振型和固有频率，改善横梁的动态特性。本文在对动横梁进行模态和能量分析的基础上，找出动横梁惯性能和弹性能的分布，基于能量平衡原理对动横梁进行结构优化，最后以能量分布的均匀性作为其结构优化的验证。曾经哈工大的张宗兰建立机床集中质量的模型，进行模态计算，得出能量分布情况，通过结构的改进达到机床内部刚度和质量配置的最优化，提高机床的动态性能［4］。浙江工大的翁泽宇依据结构动态系统的能量平衡，对平面磨床进行动态特性分析，找出其薄弱环节，改善其动态性能［5］。

1 动横梁能量计算与优化原则

本文的工程实例中，应该把动横梁的机械结构系统简化为多自由度振动系统，其运动方程为［6］:

振动能量的准确计算是解决结构问题的前提。动横梁看作是无阻尼振动系统，其振动产生的能量主要为惯性能和弹性势能。弹性势能等于弹性体在外力使之变形所做的功。在ANSYS中，模态分析中将所有非线性问题转换为线性问题进行分析。所以模态分析中单元的惯性能和弹性势能计算表达式分别为［7］:

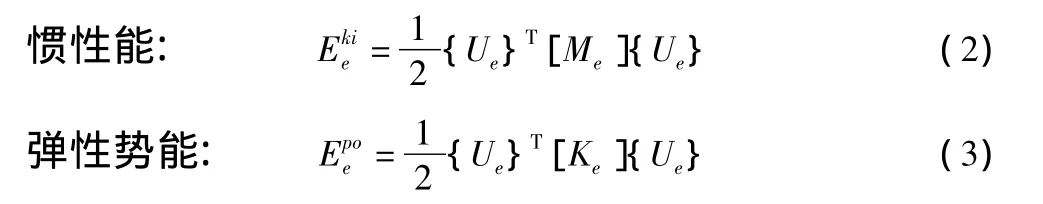
式中，［Me］为单元质量矩阵，{Ue}为单元振型向量，［Ke］为单元刚度矩阵。

结合公式(2)、(3)通过对动横梁的模型进行有限元分析，得出其惯性能和弹性势能的分布图，能量分布率高的部分可知其质量过大或者刚度偏低。惯性能分布率高的结构，应该减少该部分的质量，弹性势能分布率高的结构，应该提高其结构刚度，优化结构的质量与刚度配置，使动横梁的整体能量分布趋于均匀，这是基于能量平衡的动横梁优化设计的原则。

大型龙门加工中心的动横梁是连接主轴(Z向)和立柱床身关键部件。加工过程中，动横梁两端靠导轨面固定在立柱上，随立柱在X向进给，同时滑枕可以在横梁上完成Y向的进给，动横梁本身也可在立柱上进行Z向运动。由此可见，动横梁的形变和动态特性会直接影响龙门加工中心的加工精度。

横梁的振动特性决定其动态特性，可以通过固有频率、动刚度、阻尼比、动柔度等来表征。而基于能量平衡的动横梁动态特性分析，不需要考虑各个因素的影响因子大小的，而是以能量分布的均匀性表征动横梁的动态特性，衡量动横梁结构的质量与刚度配置是否合理。

在动横梁有限元模型的基础上，对其进行约束模态分析，获取前六阶固有频率和振型，初步判断横梁的刚度薄弱环节。然后完成动横梁的能量分析，得到动横梁的惯性能和弹性势能的等值线图，判断能量集中区域，结合模态分析判断出横梁的薄弱环节，调整结构并且对改进结构进行验证。上述思路和过程如图1所示。

图1 动横梁优化流程图

2 基于能量平衡的横梁优化过程

介绍了能量平衡原理应用于动横梁结构优化的方法，根据上述的动横梁优化思路和方法，在ANSYS经典环境下完成整个分析和优化过程。

2.1 建立有限元模型

本文采用solid works软件进行动横梁的三维实体建模，对小凸台、小孔和小的倒角进行合理简化，将三维实体模型导入ANSYS经典环境中，转换为有限元模型，设置模型主要参数，并划分网格，如表1和图2。

表1 动横梁有限元模型的主要参数

图2 动横梁有限元模型

2.2 模态分析

完成动横梁的有限元模型的建立之后，可以对动横梁进行模态分析。理论上，任何连续弹性体都有无数个固有频率，但是用有限元分析时，阶数越高，误差越大，对实际结构有意义的是较小的若干阶频率，所以只进行前六阶模态分析，等值线图如图3所示，固有频率结果如表2。

图3 模态分析前六阶振型

表2 动横梁的固有频率和相对形变

模态分析结果可以初步看出第三阶形变最大，属于危险模态，X向刚度不足，虽然第5、6阶的形变较大，但作为横梁主要工作区域的中间部分没有明显的变形，属于安全的振型，只需考虑前四阶振型。

提高频率减小振幅的方法是提高薄弱环节的刚度。然而振动也是能量的一种变现形式，促使能量分布均匀，能够达到动横梁振幅减小，频率提高的目的。

2.3 能量分析

为了能准确找到动横梁的薄弱环节，并利用能量平衡原理对动横梁进行优化，需要对动横梁进行能量分析。弹性势能集中的部位其刚度较差，惯性能分布集中的部分质量分布过大。

分析的具体过程是在模态分析中勾选计算单元结果的选项，后处理阶段应该定义单元表，添加各阶的惯性能和弹性势能。图4、图5分别为动横梁的惯性能和弹性势能分布图。

图4 前四阶动横梁惯性能分布图

图5 前四阶动横梁弹性势能分布图

通过前四阶的弹性势能分布图，可以得出靠近旋转螺母的安装面地方势能分布集中，并出现最大值，说明该处为动横梁最薄弱位置，应该加强刚度。动横梁的惯性能重要分布在横梁的中间部分，并且图5显示中间部分的弹性能分布率低，刚度较好，可以得出中间部分质量集中，应该减轻该部分质量，使能量分布均匀，提高动态特性。

3 动横梁结构改进

完成对动横梁的模态分析和能量分析，找到动横梁的薄弱环节，然后对动横梁进行了结构的改进。图6为改进前的横梁模型，图7为经过优化之后的图形模型。

图6 改进前动横梁三维模型

结合图4和图5，动横梁中间筋板的惯性能分布集中，而弹性势能分布率相对较低，采取对其进行矩形掏空;动横梁靠近导轨面的部位势能相对集中，刚度偏低，在四个角加上三角筋并加上一条Y向的纵向筋板。根据能量平衡原理，改进后需要进行能量分布均匀性的验证，看能否提高动横梁的动态特性。

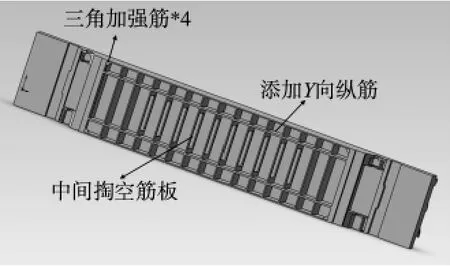
图7 改进后动横梁三维模型

4 改进后动横梁的动态特性验证

对改进后的动横梁模型进行模态分析和能量分析验证，看结构是否得到了优化。图8、图9即为动横梁进行能量分析验证的惯性能和弹性势能的分布图，表3为动横梁惯性能和弹性势能最大值的变化表。

图8 前四阶动横梁弹性势能分布图

图9 前四阶动横梁弹性势能分布图

改进之后的第3、4阶惯性能和弹性势能的最大值都有显著的下降，虽然第1、2阶的惯性能的最大值没有减小，但是从等值线图可以看出，能量集中的部位减少了，也显示能量分布更为均匀。弹性势能等值线图也发现已经有效的加强了横梁的薄弱环节，弹性势能分布也趋于均匀化。对改进后的动横梁进行模态分析的验证，也发现各阶固有频率都有相对的提高，振动有所降低，如表4所示。基于能量平衡原理完成的结构改进提高了动横梁的动态特性。

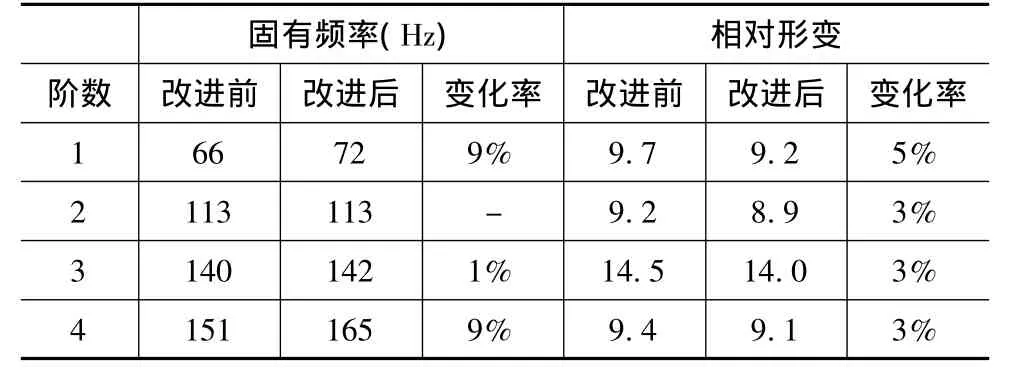
表4 动横梁改进前后固有频率和形变变化

5 结论

能量平衡原理是结构动态设计的重要理论。本文将其有效的运用到动横梁的设计和结构优化，具有很强的实用性。

以能量分布的均匀性作为动横梁的动态特性的表征，在模态分析和能量分析的基础上，通过结构的改进，有效的提高了动横梁的动态特性，达到了结构优化的目的。

将能量平衡原理和有限元技术的结合进行动横梁的动态特性分析，为结构优化设计提供了一个新方向。由于在能量均匀性上还没找到一个更为科学的表示，结构设计存在多目标性，因此在结构动态优化设计上还有很多问题亟待解决。

［1］王晓煜，贾振元，杨帆，等.龙门加工中心横梁部件的拓扑优化设计与分析［J］.制造技术与机床，2009(11):64－68.

［2］兰铁军，刘德栋，段周波，等.基于TOP＆DXVT的立式加工中心横梁复合优化设计［J］.组合机床与自动化加工技术，2011，(5):89 －92.

［3］杜钟魁，李兴山，王军.TX1600镗铣加工中心横梁的动态特性分析［J］.沈阳理工大学学报，2010，29(4):1－4.

［4］张宗兰.能量平衡法在机床结构动态参数优化中的应用［J］.哈尔滨工业大学学报，1987，12(4):37 －43.

［5］翁泽宇，张南南，蔡勇，等.有限元技术在基于能量平衡的机床动态设计中的应用［J］.机械强度，1987，33(3):411 －417.

［6］韩清凯，于涛，孙伟.机械振动系统的现代动态设计与分析［M］.北京:科学出版社，2010.

［7］蔡勇.基于能量平衡原理的机床动态设计技术研究［D］.浙江:浙江工业大学，2010.

［8］吴长智，郑兆瑞，沈明，等.MG1432B整机薄弱环节分析［J］.机械强度，1992，14(4):51 －56.

［9］郑伟中.用能量平衡原理分析砂轮架的动态特性［J］.机床，1982(1):34－37.