解周期性微分方程的三角拟合显式两步方法

刘石威，刘文

(1.枣庄学院 数学与统计学院，山东 枣庄 277160；2.枣庄市 第四十一中学，山东 枣庄 277100)

0 引言

下面格式的二阶微分方程问题一直广受人们关注：

(1)

尤其当它的解具有一定的周期性或振荡性时.在化学物理学、物理化学、电子学、量子力学、天体力学等不同的领域中这类问题经常出现，如果不能求出这类问题的解析解，那么求它的数值解显得尤为重要.而三角拟合是其中较常使用的方法.Gautschi[1]与Lyche[2]首先给出此项技术的理论基础，后来Raptis和Allison[3]针对二阶微分方程构造了一个Numerov类型的指数拟合方法，新方法对于解Schrödinger类型的方程具有更高的效率.

1 三角拟合Störmer-Verlet二步方法

对于求数值解的问题，我们考虑下面形式的显示两步格式：

yn+1=α1yn+α2yn-1+h2(α3f(xn,yn)+α4f(xn-1,yn-1)),

(2)

这个格式可以在[4]中找到.

让方法(2)精确积分下面函数的线性组合:

{cos(ωx),sin(ωx)}

(3)

可得如下方程组：

(4)

在这里u=ωh.

α4=0.

(5)

上面系数的泰勒展式为:

α4=0.

(6)

以(5)所给系数的三角拟合Störmer-Verlet两步方法记为ST2F1，该方法的局部截断误差为:

(7)

因此这个方法的代数阶为2.根据(6)，因为u=ωh,可知当ω→0时，所得到的新方法ST2F1将变为原始的Störmer-Verlet两步方法.

2 相属性与稳定性分析

将得到的新方法应用到试验方程：

y″=λy,

(8)

可得到差分方程：

yn+1-2S(H2,u)yn+yn-1=0,

(9)

其中，S(H2,u)=(2-α3H2)/2,

H=λh，α3由(5)给出.

定义1:对于含S(H2,u)的新方法ST2F1，称

φ(H2,u)=H-arccos(S(H2,u)),

为相滞.

称ST2F1的相滞阶数为q，当

φ(H2,u)=O(Hq+1).

作替换k=H/u,k∈□,k≠1,此时这个新方法的相滞可以表示为

因此，这个新方法的相滞阶数为2.

定义2:称一个在平面H-u內的二维平面区域D为含有S(H2,u)的方法ST2F1的绝对稳定性区域，当对于所有的(H,u)∈D，满足

|S(H2,u)|<1,

并称满足

|S(H2,u)|=1.

的封闭曲线为绝对稳定区域边界.

在图1中，我们给出新方法ST2F1的绝对稳定性区域.

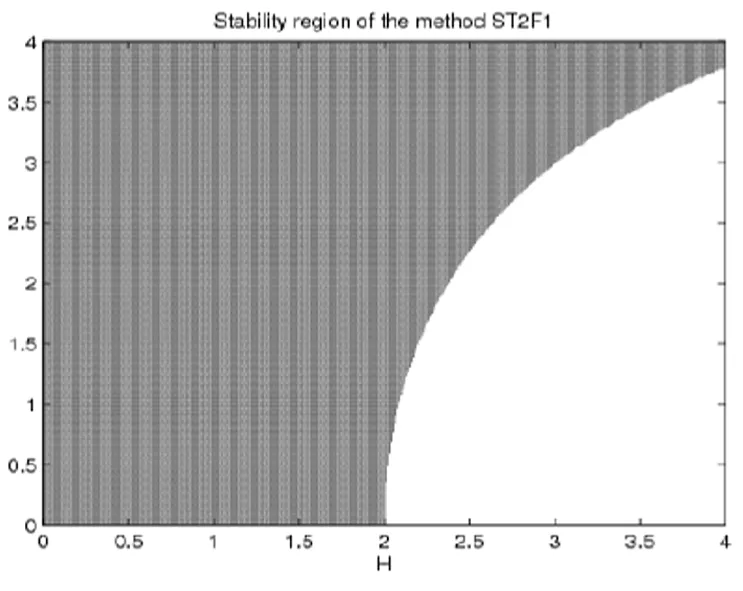
图1 新方法ST2F1的绝对稳定性区域

3 数值实验

本节将新方法应用于解四个振荡问题，前三个是非齐次方程，最后一个是双频类周期问题.

选用下列四个方法予以比较:

原始的Störmer-Verlet二步方法，见[4]，用ST2表示.

三角拟合Störmer-Verlet二步方法，即本文所得到的新方法，用ST2F1表示.

原始的Störmer类型的三步方法，见[4]，用ST3表示.

FSAL属性的RKN方法，见[5]，用FRKN表示.

3.1 非齐次方程

求解下面问题:

y″=-100y+99sin(x),
y(0)=1,y′(0)=11.

(10)

其精确解为y(x)=cos(10x)+sin(10x)+sin(x).

对方程(10)做数值实验，我们选择区间0≤x≤100,针对于新方法ST2F1和FRKN选择ω=10.评价的标准是比较四个方法的全局误差及计算所用的步长，在图2中我们给出数值演示结果.

3.2 非齐次方程

求解下面问题:

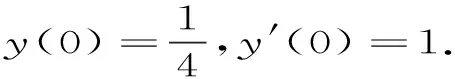
(11)

对方程(11)做数值实验，我们选择区间0≤x≤100,针对于新方法ST2F1和FRKN选择ω=9.评价的标准是比较四个方法的全局误差及计算所用的步长，在图3中我们给出数值演示结果.

3.3 非齐次方程

求解下面问题:

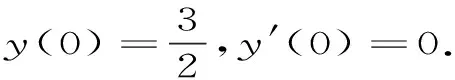
(12)

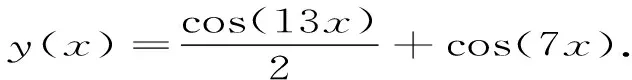
对方程(12)做数值实验，我们选择区间0≤x≤100,针对于新方法ST2F1和FRKN选择ω=13.评价的标准是比较四个方法的全局误差及计算所用的步长，在图4中我们给出数值演示结果.

3.4 双频类周期问题

求解下面问题:

y″=-169y+(480-160i)e3ix,
y(0)=4+i,y′(0)=-23+22i.

(13)

它等价于

u''(x)+169u(x)-480cos(3x)-160sin(3x)=0,

v''(x)+169v(x)-480sin(3x)+160cos(3x)=0.

其中y(x)=u(x)+iv(x).

其精确解为

u(x)=-2sin(13x)+cos(13x)+3cos(3x)+sin(3x),

v(x)=sin(13x)+2cos(13x)+3sin(3x)-cos(3x).

对方程(13)做数值实验，我们选择区间0≤x≤100,针对于新方法ST2F1和FRKN选择ω=13.评价的标准是比较四个方法的全局误差及计算所用的步长，在图5中我们给出数值演示结果.

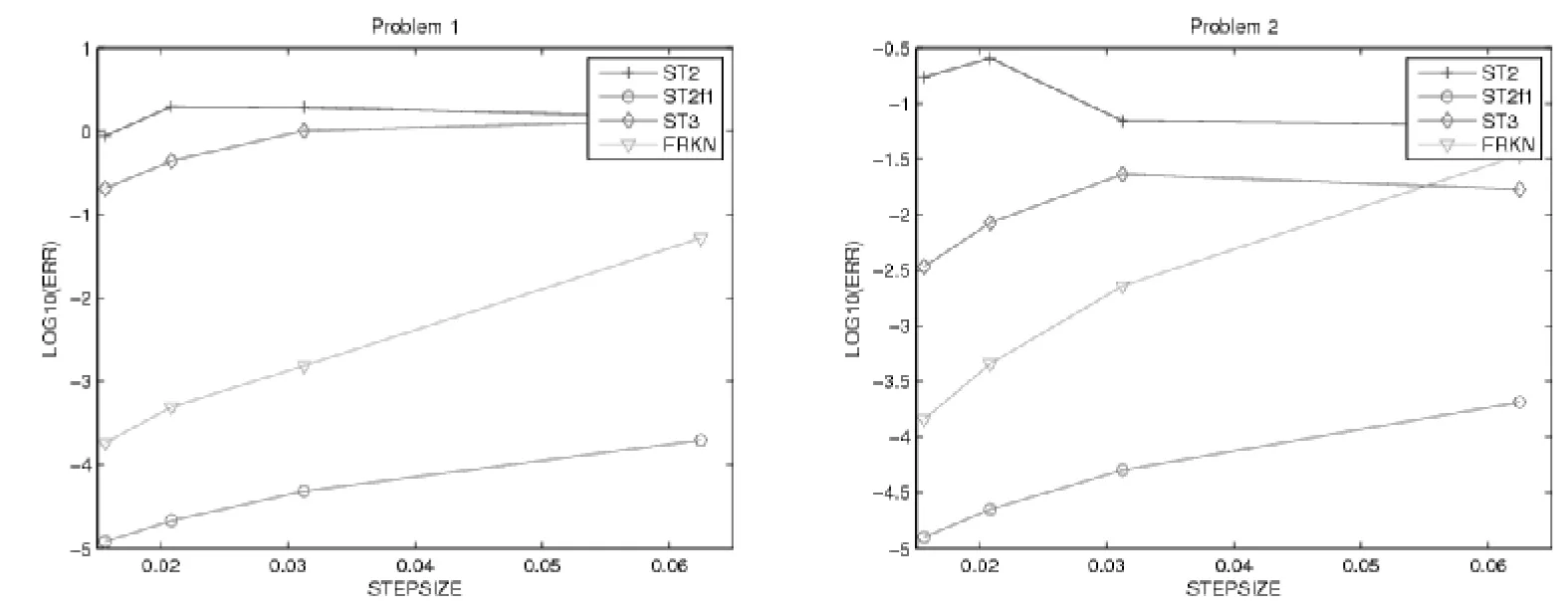
图2 问题4.1数值演示结果 图3 问题4.2数值演示结果

Fig.2EfficiencycurvesinProblem4.1Fig.3EfficiencycurvesinProblem4.2

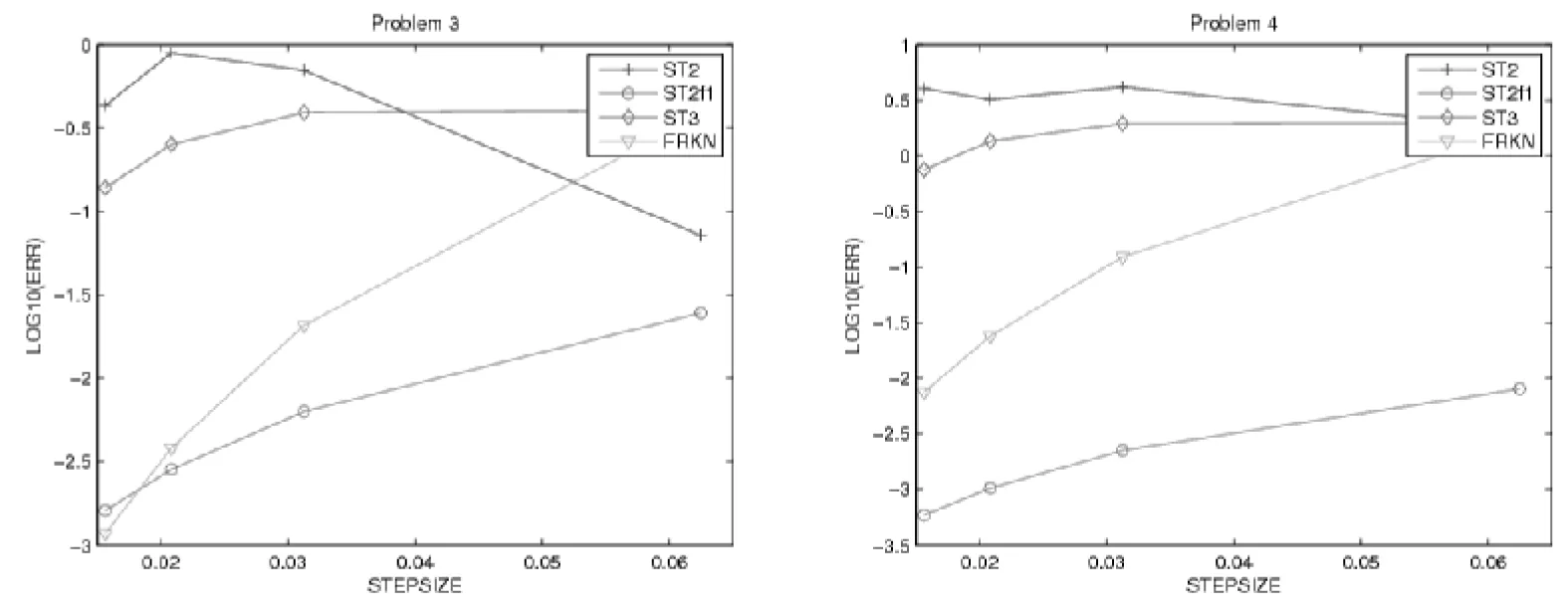
图4 问题4.3数值演示结果 图5 问题4.4数值演示结果

Fig.4EfficiencycurvesinProblem4.3Fig.5EfficiencycurvesinProblem4.4

5 结论

从数值实验的结果可知，三角拟合Störmer-Verlet显式二步方法在求解带初值的振荡问题时较其它三个方法更为高效.这是因为这个三角拟合方法能精确积分{cos(ωx),sin(ωx)}的线性组合，而其它的方法不具有这个特性.

参考文献

[1]Gautschi W. ,Numerical integration of ordinary differential equations based on trigonometric polynomials[J],NumerischeMathematik, 1961:381-397.

[2]Lyche T.,Chebyshevian multistep methods for ordinary differential equations[J].NumerischeMathematik, 1972:65-75.

[3]Raptis A., Allison A.,Exponential-fitting methods for the numerical solution of the Schrodinger equation[J].ComputerPhysicsCommunications,1978: 1-5.

[4]Lambert J.D, Computational methods in ordinary differential equations[M].John Wiley & Sons Inc, New York, 1973.

[5]Van de Vyver H.A Runge-Kutta-Nyström pair for the numerical integration of perturbed oscillators, Computer Physics Communications, 2005:129-142.