技术进步对中国碳排放的影响——基于向量误差修正模型的实证研究

李凯杰，曲如晓

(北京师范大学经济与工商管理学院，北京 100875)

一、引言

1978年改革开放以来，中国经济快速发展，与此同时，能源消费和污染排放量也在不断增加，据荷兰环境评估局(MNP)的评估报告，2006年中国碳排放达到62亿吨，超过美国，成为第一排放国，2007年为67.2亿吨，占世界总排放的24.3%，增量占世界总增量的近60%，中国受到的国际减排压力与日俱增［1］，减少碳排放成为中国未来的主要任务之一。技术进步是影响碳排放的关键因素，其对碳排放的影响受到了越来越多的重视。技术进步可以促进能源强度降低减少碳排放［2］，同时也会推动经济增长增加碳排放，那么中国技术进步对碳排放影响如何?是否有效地减少了碳排放?本文将尝试对此做出回答。分析技术进步对中国碳排放的影响有助于深入了解碳排放变化的影响因素，为科学制定减排政策提供依据，具有重要的学术价值和现实意义。

早期的技术进步对环境影响的研究多是在假定技术进步外生的新古典增长模型框架内展开。Nordhaus(1977)［3］分析了外生技术进步下经济增长对环境的影响，之后于1993年［4］构建了气候变化和经济的动态综合模型(DICE)，用于分析经济增长和环境的相互关系。但是部分研究表明，技术进步不是外生的，多数技术进步是内生的，受需求的影响［5］。Newell等(1999)［6］发现能源价格对技术进步有显著影响，证实了内生技术进步的存在。之后涌现了大量分析内生技术进步对环境影响的研究。Goulder和 Schneider(1999)［7］利用可计算模拟一般均衡模型(CGE)分析了存在引致技术进步时减排成本的变化，发现存在引致技术进步时，实现减排目标所需成本更低。Nordhaus(2002)［8］构建了R＆DICE模型比较了引致技术进步与要素替代对碳排放的影响，发现技术进步对碳排放的影响要小于要素替代弹性的影响。Buonanno等(2003)［9］在RICE模型中引入了技术进步，发现技术进步可以显著降低减排成本，Popp(2004)［10］构建了 ENTICE 模型，即考虑内生技术进步的DICE模型，发现忽略引致技术进步会高估减排成本。Grimaud 和 Rouge(2008)［11］、Acemoglu等(2010)［12］以及 Smulders 和 Di Maria(2011)［13］均考虑了内生技术进步对碳排放的影响。国内研究主要集中于分析影响中国碳排放变化的因素。彭水军等(2006)［14］把与环境相关的科研课题经费投入和政府财政科研支出作为技术进步变量，发现技术进步导致中国污染排放增加。徐国泉等(2006)［15］、王锋等(2010)［16］运用类似的指数分解法分析了中国人均碳排放的影响因素，结论有所不同，前者认为经济发展对中国人均碳排放的贡献率成指数增长，而能源效率和能源结构对抑制中国人均碳排放的贡献率呈倒“U”型;后者发现中国碳排放增长的主要正向驱动因素为人均GDP、交通工具数量、人口总量、经济结构和家庭平均年收入;主要负向驱动因素为生产部门能源强度、交通工具平均运输线路长度、居民生活能源强度。孙建卫等(2010)［17］采用Laspeyres指数分解方法对碳排放量和碳排放强度及其变化因素进行了分析，认为GDP增长是碳排放总量增加的主要动力，技术进步因素是碳排放量降低的主导因素。林伯强等(2010)［18］运用协整的方法研究了现阶段碳排放的影响因素，发现能源消费强度、能源强度和城市化水平会影响中国碳排放。

综上，国内外已有很多关于技术进步与碳排放关系的研究，但是这些研究多是从静态角度考察当期技术进步对碳排放的影响，未分析技术进步的累积影响。实际中，技术进步从新技术产生到技术的扩散和应用需要经历较长的时间，仅从静态角度分析会低估技术进步的作用，不能揭示技术进步对碳排放的长期影响及动态关系。基于此，本文构建非结构化的多方程模型，应用向量误差修正模型(Vector Error Correction Model，VEC模型)分析技术进步和中国碳排放的长短期动态关系。

二、研究方法和数据

(一)研究方法

Kaya(1989)［19］通过因式分解的方法将温室气体排放与人口、经济发展水平、技术进步和单位能源消费联系起来，提出了Kaya恒等式。本文在Kaya等式基础上建立如下非结构方程来考察碳排放和技术进步的长期均衡关系:

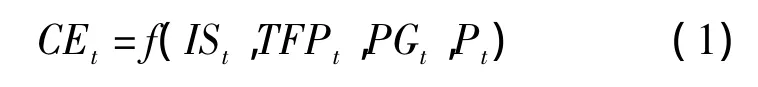
其中，CEt、ISt、TFPt、PGt和 Pt分别表示碳排放量、能源结构碳强度、技术进步、人均GDP和人口。

通过上述非结构化方程，可以得到向量自回归模型。向量自回归(VAR)模型是把系统中每一个内生变量作为系统中所有内生变量的滞后值的函数，能较好地对具有相关性的时间序列系统进行预测，并可考察扰动项对变量系统的动态影响，其表达式如下:

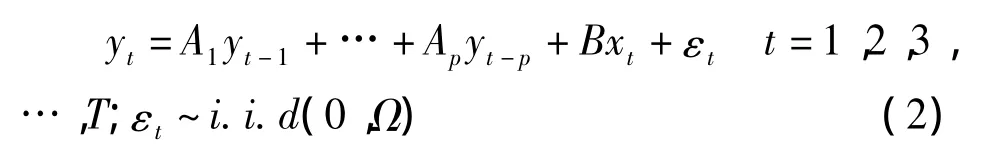
其中，yt是k维内生变量向量，xt是d维外生变量向量，p是滞后阶数，T是样本个数。A1，…，Ap和B是待估计系数矩阵，εt是随机扰动向量，为零均值独立同分布的白噪声向量。如果所选取的变量是平稳时间序列，可以直接使用VAR模型估计;但如果变量不平稳，就要考虑采用VEC模型，VEC模型要求变量间存在协整关系，可以认为VEC模型是含有协整约束的VAR模型，多用于具有协整关系的非平稳时间序列模型。

上式可以写为:

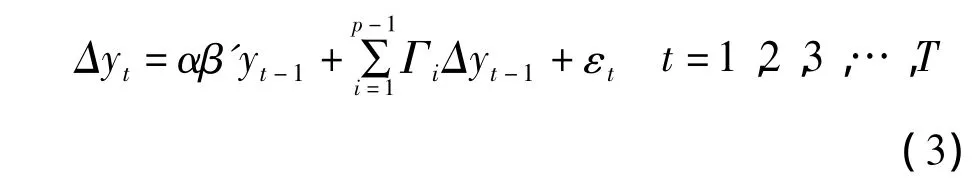
式中每个方程的误差项都具有平稳性，用误差修正模型表示为:

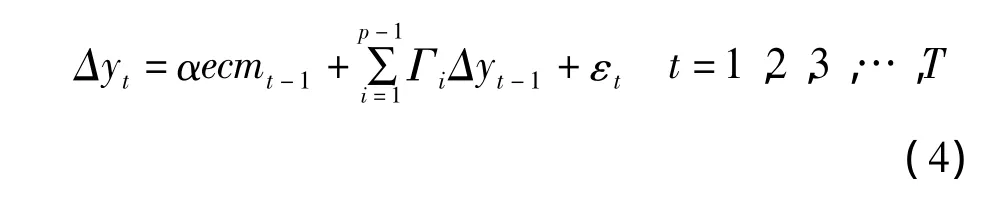
其中，ecmt-1=β'yt-1是误差修正项，反映变量间的长期均衡关系，系数矩阵α反映了变量间偏离长期均衡状态时，将其调整到均衡状态的调整速度，所有作为解释变量的差分项的系数反映各变量的短期波动对作为被解释变量的短期变化的影响。

(二)变量选取和数据来源

(1)碳排放量(CEt)，数据来源于二氧化碳信息分析中心(Carbon Dioxide Information Analysis Center，CDIAC，http://cdiac.ornl.gov/)。

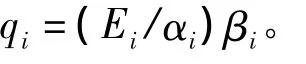
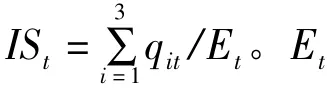
(3)技术进步，用全要素生产率(TFPt)来衡量。技术进步是一个无形的变量，无法直接进行度量，目前文献中通常采用三种指标间接度量技术进步:一是R＆D投入，二是专利数量，三是全要素生产率(Total Factor Productivity，TFP)。统计年鉴上只有近几年中国分省区的R＆D投入数据，基于数据的可得性，本文没有选取R＆D投入;专利数也很难准确反映技术水平，因为某一个专利价值可能要远远高于其它专利的，一个专利价值可能是几个甚至几十个专利价值之和。最终，选取全要素生产率度量技术进步。全要素生产率最早由索洛［20］提出，是指要素投入之外的技术进步等导致的产出增加，是剔除要素投入贡献后得到的残差，又称索洛余值，用来反映生产者的技术水平。利用索洛余值表示全要素生产率有一个隐含假设，所有生产者技术上都是有效的，但实际情况并非如此。数据包络分析法(DEA)允许技术无效率的存在，因此广泛地用于全要素生产率［21］、碳排放影子价格［22］以及能源效率［23］等估算。本文选取基于动态非参数前沿生产面的DEA-Malmquist生产率指数方法来测算全要素生产率，该方法是根据包含多个决策单元的平衡面板数据，应用投入产出数据，识别出技术效率最好的经营决策单位，以其为基础构造生产前沿面，通过生产过程的实际投入或产出值与最优值的比较得出技术效率水平指数。Malmquist指数又可分解为技术效率变化指数和技术进步指数。DEA-Malmquist指数法的关键是投入和产出变量的选取。要素投入选取物质资本和劳动力两个指标，物质资本用各地区资本存量表示，劳动力指标选择各地区从业人口数量，产出指标用经过价格指数(1978=100)平减的地区GDP表示。劳动力和产出数据均来源于历年《中国统计年鉴》和《新中国55年统计资料汇编(1949-2004)》。资本存量数据借鉴张军等(2004)［24］所采用的“永续盘存法”进行估算。张军等人是以1952年价格估算的各省资本存量，本文的基期为1978年，因此需要以1978年价格重新估算的各省资本存量。选取各省1978年固定资本形成总额除以10%为其初始资本存量;统计年鉴上没有1990年之前的固定资产投资价格指数，选取各省零售价格指数来代替;其余指标选取及估算方法均和张军等(2004)［24］相同。将中国29个省、自治区和直辖市①为保持口径统一将1996年开始分离的重庆数据并入四川省，西藏则因数据缺乏不包括在样本内。作为决策单元，采用投入导向的DEA方法，运用DEAP2.1软件，得到全国以及各地区每年Malmquist生产率指数。具体结果见表1，限于篇幅，只列出了样本期内全国各省及东、中、西部地区②东部地区包括北京、天津、河北、辽宁、上海、江苏、浙江、福建、山东、广东、海南11个省市。中部地区包括山西、吉林、黑龙江、安徽、江西、河南、湖北、湖南8个省。西部地区包括内蒙古、广西、四川、贵州、云南、陕西、甘肃、青海、宁夏、新疆10个省自治区。的平均Malmquist生产率指数。

(4)人均GDP(PGt)，反映了经济体的经济发展水平，不同的经济发展水平其碳排放量也有所不同，用经过价格指数(1978=100)平减的实际人均GDP表示，数据来源于历年《中国统计年鉴》。

(5)人口(Pt)，人口变化会对碳排放带来显著的影响，人口的增加可能会带来碳排放量的增多，人口数据来源于历年《中国统计年鉴》。

本文样本区间为1978-2008年。为避免数据的剧烈波动并消除时间序列中存在的异方差现象，对各个变量数据分别取自然对数，记为:lnQt、lnISt、lnTFPt、lnPGt和 lnPt。

三、模型估计和结果分析

(一)平稳性检验

现代计量经济学要求计量模型建立在变量平稳的基础上，而现实中许多经济变量通常不是平稳的，使用传统的计量经济学方法易产生“伪回归”问题。因此，首先要对变量进行平稳性检验，确定其平稳性及单整阶数。常用的方法有扩展的Dichey-Fuller(ADF)和非参数的PP法，本文采用ADF检验，结果见表2。

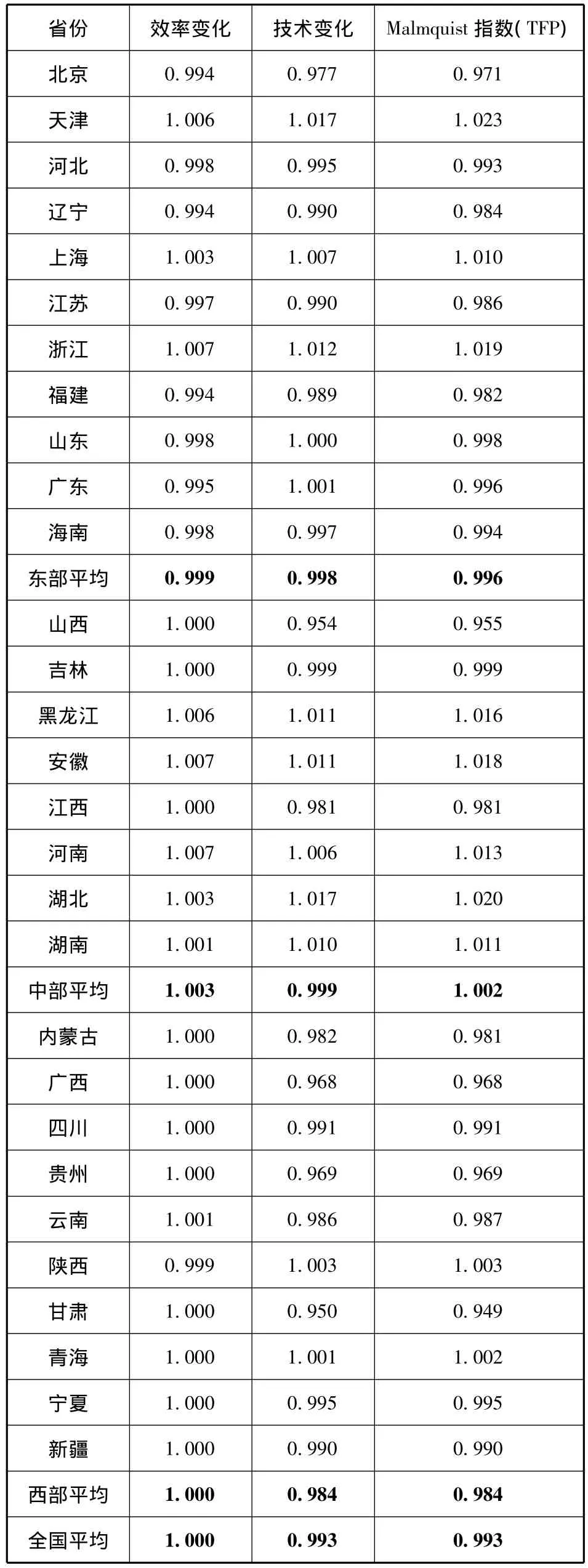
表1 中国各省1978-2008的平均Malmquist指数

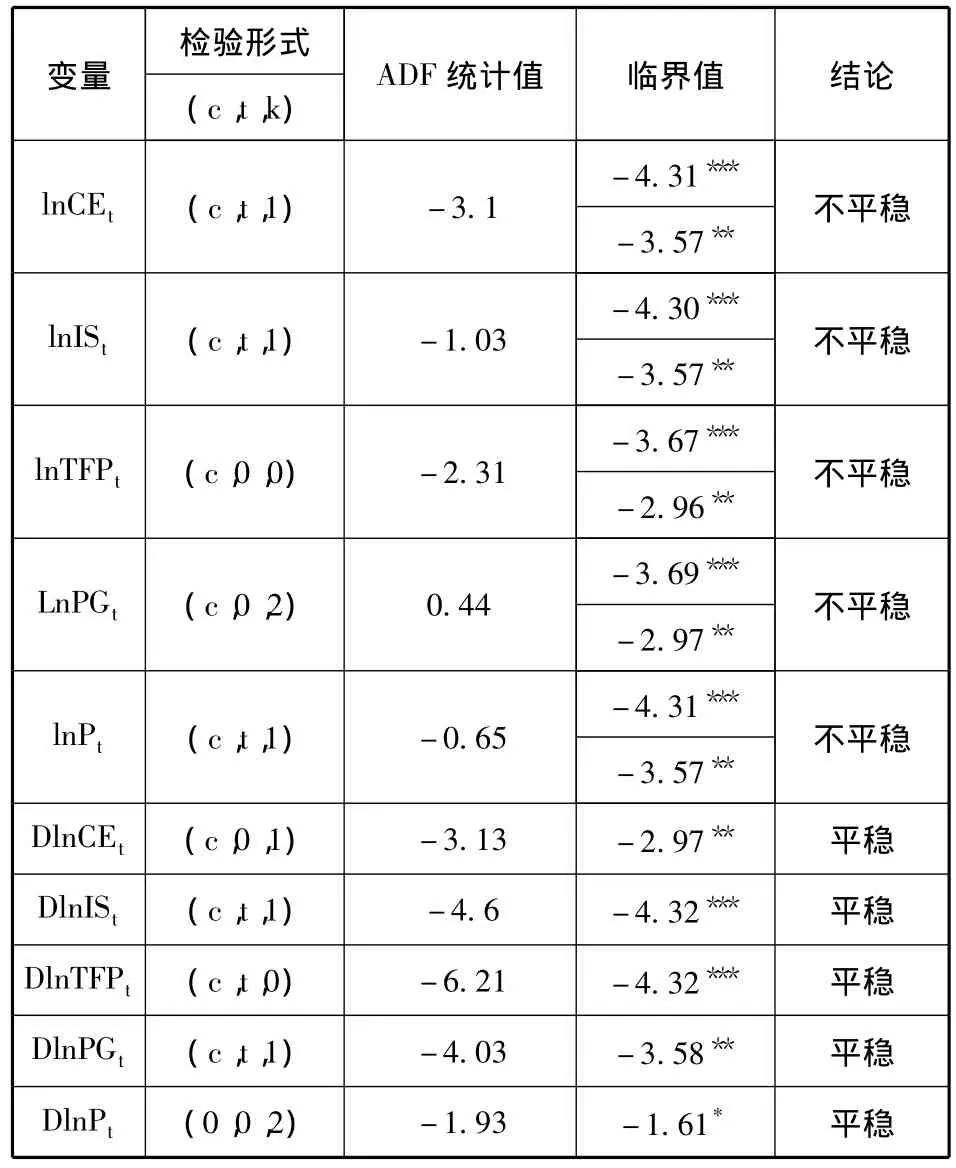
表2 ADF平稳性检验结果

由检验结果可以看出，变量 lnCEt、lnISt、lnTFPt、lnPGt和 lnPt在1%和5%的显著性水平下的ADF统计值都大于其相应的临界值，表明五个变量都是非平稳的，而其相应的一阶差分序列ADF统计值都小于临界值，表明五个变量的差分序列是平稳的，即这些变量是一阶单整的。

(二)协整检验

建立VEC模型前，首先要验证变量间是否存在协整关系，只有存在协整关系的变量才可以建立VEC模型。时间序列分析中，每一个序列单独来说可能是非平稳的，但这些序列的线性组合却可能有不随时间变化的性质，这种平稳的线性组合说明变量间是协整的，意味着这些非平稳变量之间存在长期稳定的均衡关系。协整检验要求变量是单整变量，且单整阶数相同，由上述平稳性结果知所有变量均为一阶单整变量，因此可以对变量进行协整关系分析。常用的协整检验方法主要包括基于回归残差的协整检验和基于回归系数的Johansen协整检验。前者适合对两变量的模型进行协整检验，后者适合对多变量模型的协整检验，本文采用Johansen极大似然法对多变量系统进行协整检验。

在进行Johansen检验之前，首先要确定VAR模型的合理滞后阶数。滞后阶数的选择既要有足够的滞后项，又要有足够的自由度，使模型具有较强的解释能力同时又能消除误差项的自相关。通过估计一个无约束VAR模型并使用赤池(AIC)和施瓦茨(SC)信息准则来选取最优的滞后阶数，通过多次检验发现，当滞后阶数为2时，AIC和SC值最小，再结合LR统计量，最终选定无约束VAR模型的最优滞后阶数为2。基于VAR模型的协整检验滞后期是无约束VAR模型一阶差分变量的滞后期，因此确定协整检验的滞后期为1。根据数据特点，选取序列有线性趋势但协整方程只有截距的检验形式。协整检验结果见表3。结果显示，在不存在协整方程和最多存在一个协整方程的原假设下，迹统计量值均大于5%显著水平的临界值，而其他假设条件下的迹统计量都小于5%水平的临界值，所以接受变量间存在两个协整关系的假设，最大特征值检验也得到同样的结论，综上，变量间存在两个协整关系，根据经过标准化后的协整系数，选取一个能准确反映变量间关系的协整方程，其表达式为(括号内为标准差):

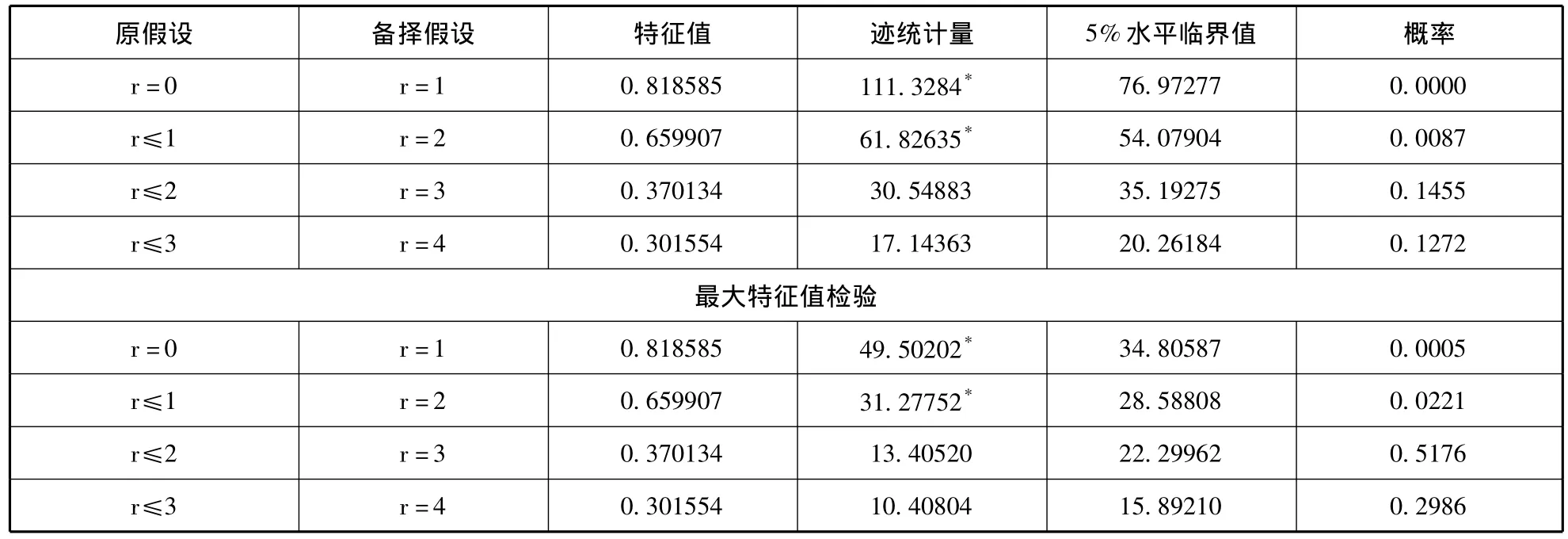
表3 Johansen协整检验结果

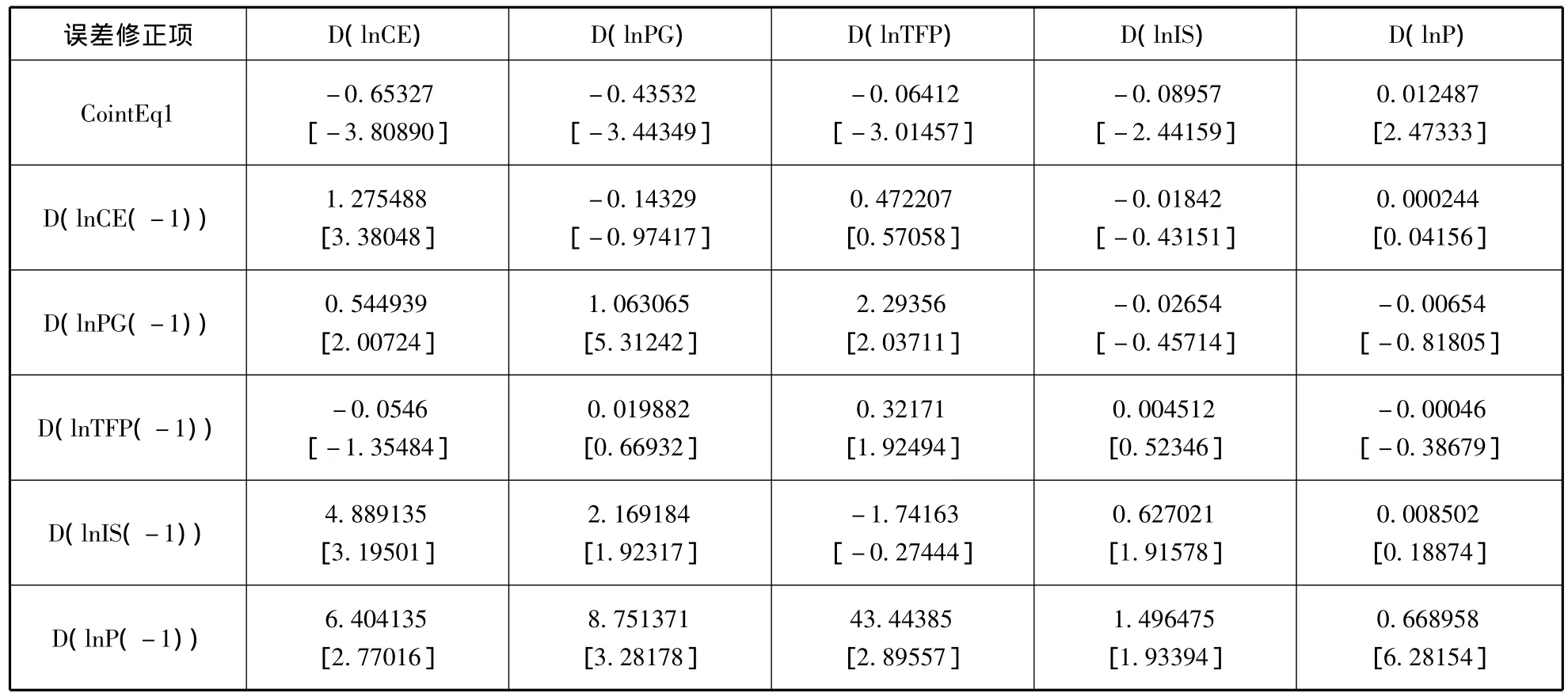
表4 向量误差修正模型估计结果

其中ecm为误差项，需要对误差项进行单位根检验以确定协整关系的平稳性，ADF检验结果显示，误差项的ADF统计量值为-3.28，小于5%显著水平的临界值-2.97，所以其在5%显著水平下是平稳的，即协整关系平稳有效。

协整方程表明，1978-2008年间，中国的碳排放总量与能源结构碳强度、技术进步、人均GDP和人口之间存在着稳定的长期均衡关系，所有变量在5%的置信水平下通过t统计量检验，且模型具有较高的拟合度。从协整结果来看，长期内，能源结构碳强度、人均GDP和人口同中国碳排放呈正相关关系，技术进步同碳排放呈负相关关系。能源结构碳强度、人均GDP和人口每变动1个百分点，分别带动碳排放同向变动4.53、2.07和1.55个百分点;全要素生产率每变动1个百分点，带动碳排放相反方向变动1.75个百分点。这和国内大部分研究结论基本一致，能源结构碳强度、人均GDP和人口的增加提高了碳排放，技术进步则减少了碳排放。

(三)向量误差修正模型

如果系统变量不平稳，不能直接利用VAR模型来考察变量之间的关系。VEC模型可以较好地克服VAR的不足，系统变量不平稳且存在协整关系时可以通过建立VEC模型来考察变量间的相互调整速率及短期互动影响并观察变量间的因果关系。在进行VEC检验之前，先对模型的平稳性进行检验，通过检验，发现所有特征根均落在单位圆内或圆上，表明VEC模型稳定，模型得出的结果也较为可靠。表4为向量误差修正模型的估计结果。

由表4估计结果可知，模型误差修正项系数为负，说明模型具备误差修正机制，进一步证明了各变量之间的长期均衡关系。

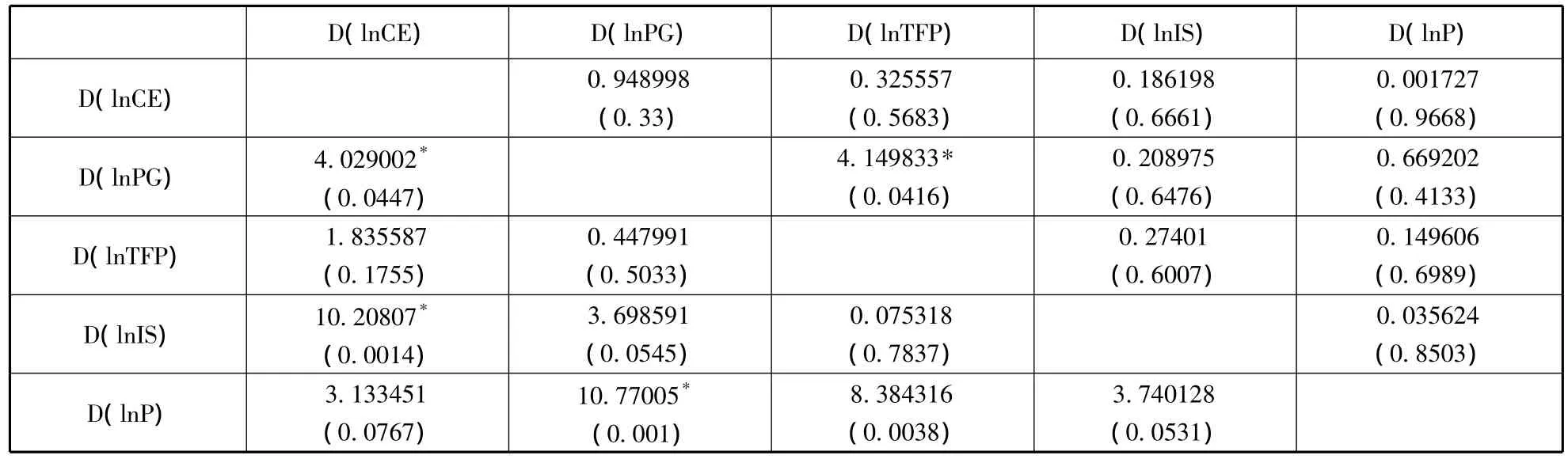
表5 Granger因果检验结果

短期来看，(1)人均GDP、能源结构强度和人口的增加都会增加碳排放，且效果显著;而全要素生产率的提高会降低碳排放，但t统计量的值不显著，即短期技术进步对碳排放的影响效果不明显，这可能是因为技术进步对碳排放的影响要考虑其时滞和积累问题，在短时期内很难将技术进步快速转变为碳排放的减少。(2)人均GDP受到能源结构的影响，其他变量的影响不显著。因为目前中国正处于工业化阶段，主要的燃料仍以化石燃料为主，经济的发展离不开能源的大量消费，所以能源结构的提高(即煤、石油、天然气等化石燃料在整个能源结构中比重上升)推动了人均GDP的增加;技术对人均GDP影响不显著是因为创新需要一段时间的积累，且创新后的扩散和应用却要经过很长时间才能体现出来，短期内技术进步对人均GDP的作用还不能显现出来。(3)人均GDP增加会推动技术进步。随着经济发展，对创新的要求越来越高，会推动一国技术水平的不断进步。碳排放、能源结构强度和人口的变化对技术没有显著影响。

(四)基于向量误差修正模型的格兰杰(Granger)因果检验

协整关系的存在并不表明变量之间必然存在有经济意义的因果关系，需要用Granger因果检验来考察变量间的因果关系。Granger因果检验要求变量必须是平稳的，直接对时间序列进行Granger因果检验会造成伪回归，而向量误差修正模型中的变量具有平稳性特征，从而保证了Granger因果检验的有效性。因此可以采用基于向量误差修正模型的Granger因果检验来考察变量间的短期关系，结果见表5。

由Granger因果检验结果可知，短期内人均GDP和能源结构强度是碳排放的单向Granger原因，而技术进步则不是碳排放的Granger原因，这也验证了向量误差修正模型得出来的结论，即短期内人均GDP和能源结构强度对碳排放有显著影响，人均GDP和能源结构强度的提高会带来碳排放的增加，而技术进步对碳排放没有显著影响。人均GDP的提高是技术进步的Granger原因，这也符合误差修正模型所得出的结论，人均GDP的提高会带来技术进步。

四、结论与进一步工作

本文采用DEA-Malmquist指数测算了中国1978-2008的技术进步，在VEC模型的基础上检验了中国碳排放和技术进步之间的长短期关系，根据上述分析，得到了以下结论:

(1)中国碳排放和能源结构强度、人均GDP、技术进步和人口存在长期稳定的协整关系，能源结构强度、人均GDP和人口的增加会带来碳排放的增加，而技术进步则会减少碳排放，按影响大小依次为:能源结构强度、人均GDP、技术进步和人口。

(2)短期内，能源结构强度和人均GDP对碳排放有显著影响，而技术进步并不能显著减少碳排放。能源结构强度反应了能源结构对碳排放的影响，一旦能源结构改变，煤、石油、天然气等化石燃料在能源消费量中比重减少，清洁能源比重增加，碳排放量会明显减少;人均GDP反映了一国的经济发展水平，随着经济的发展，生产所需的资源消耗不断增加，碳排放量显著增加;技术进步短期内对碳排放没有显著影响，是因为新技术研发后的扩散使用需要较长时间，技术要经过一段时间的积累才能起到减排的作用。

未来经济增长仍是中国的主要任务，由此带来的碳排放会不断增加，因此只能通过改善能源结构和技术进步来减少碳排放。短期内，可以通过降低化石燃料消费比例，改善能源结构减少碳排放。长期内，技术进步是减少碳排放有效的手段，应加大技术研发投入，推动中国的节能技术与低碳技术的发展，加快技术的扩散速度，尽快将新能源技术投入到使用，减少碳排放。

本文采取了时间序列分析方法，且由于数据的可得性，样本区间只有31年，因此仅考虑了经济增长、能源结构、人口和技术进步的因素，而实际影响碳排放变化的因素还包括产业结构、地区差异以及政策差异等因素，未来研究可以利用面板数据控制更多的影响碳排放的因素，进一步地分析技术进步对碳排放的影响。

［1］林伯强，蒋竺均.中国二氧化碳的环境库兹涅茨曲线预测及影响因素分析［J］.管理世界，2009，(4):27-36.

［2］王淑新，何元庆，王学定.中国低碳经济演进分析:基于能源强度的视角［J］.中国软科学，2010，(9):25-32.

［3］Nordhaus W D.Economic Growth and Climate:The Case of Carbon Dioxide［J］.American Economic Review，1977，(67):341-346.

［4］Nordhaus W D.Optimal Greenhouse-Gas Reduction and Tax Policy in the DICE model［J］.American Economic Review，1993，(83):313-317.

［5］Grubb M，Chapuis T，Ha-Duong M.The Economics of Changing Course:Implications of Adaptability and Inertia for Optimal Climate Policy［J］.Energy Policy，1995，(23):417-431.

［6］Newell R G，Jaffe A B，Stavins R N.The Induced Innovation Hypothesis and Energy-Saving Technological Change［J］.Quarterly Journal of Economics，1999，(114):941-975.

［7］Goulder L H，Schneider S H.Induced Technological Change and the Attractiveness of CO2Emissions Abatement［J］.Resource and Energy Economics，1999，(21):211-253.

［8］Nordhaus W D.Modeling Induced Innovation in Climate Change Policy［J］.in Grubler，A.;N.Nakicenovic，and Nordhaus，W.D.eds.，Technological Change and the Environment:Resources for the Future Press，Washington，DC.2002.

［9］Buonanno P，Carraro C，Galeotti M.Endogenous Induced Technical Change and the Costs of Kyoto［J］.Resource and Energy Economics，2003，(25):11-34.

［10］Popp D.ENTICE:Endogenous Technological Change in the DICE Model of Global Warming［J］.Journal of Environmental Economics and Management，2004，(48):742-768.

［11］Grimaud A，Rouge L.Environment，Directed Technical Change and Economic Policy［J］.Environmental and Resource Economics，2008，(41):439-463.

［12］Acemoglu D，Aghion P，Bursztyn L，Hemous D.The Environment and Directed Technical Change［R］.NBER Working Paper，No.15451，2010.

［13］Smulders S，Di Maria C.The Cost of Environmental Policy under Induced Technical Change［R］.Environmental Economics and Climate Change Workshop Working Paper，2011.

［14］彭水军，赖明勇，包 群.环境、贸易与经济增长［M］.上海:上海三联书店，2006.

［15］徐国泉，刘则渊，姜照华.中国碳排放的因素分解模型及实证分析:1995-2004［J］.中国人口·资源与环境，2006，(6):158-161.

［16］王 锋，吴丽华，杨 超.中国经济发展中碳排放增长的驱动因素研究［J］.经济研究，2010，(2):123-135.

［17］孙建卫，赵荣钦，黄贤金，等.1995-2005年中国碳排放核算及其因素分解研究［J］.自然资源学报，2010，(8):1284-1293.

［18］林伯强，刘希颖.中国城市化阶段的碳排放:影响因素和减排策略［J］.经济研究，2010，(8):66-78.

［19］Kaya Y.Impact of Carbon Dioxide Emission on GNP Growth:Interpretation of Proposed Scenarios［R］.Presentation to the Energy and Industry Subgroup，Response Strategies Working Group，IPCC，Paris，l989.

［20］Solow R M.Technical Change and the Aggregate Production Function［J］.Review of Economics and Statistics，1957，(39):312-320.

［21］傅晓霞，吴利学.前沿分析方法在中国经济增长核算中的适用性［J］.世界经济，2007，(7):56-66.

［22］刘明磊，朱 磊，范 英.我国省级碳排放绩效评价及边际减排成本估计:基于非参数距离函数方法［J］.中国软科学，2011，(3):106-114.

［23］孙广生，杨先明，黄 祎.中国工业行业的能源效率(1987-2005)——变化趋势、节能潜力与影响因素研究［J］.中国软科学，2011，(11):29-39.

［24］张 军，吴桂英，张吉鹏.中国省际物质资本存量估算:1952-2000［J］.经济研究，2004，(10):35-44.