水流交汇区的水动力学特性数值模拟
刘盛,康 鹏 ,李 然 ,魏 娟
(四川大学水力学与山区河流开发保护国家重点试验室,四川 成都 610065)
水流交汇现象在环境工程和水利工程等领域广泛存在。水流交汇区的水流流动十分复杂,呈现诸多特有的水动力学特性,如流动混掺、水面壅高、二次流等,这些特性受到很多因素的影响,包括交汇口形状、尺寸、河道坡底、交汇角大小、流量比、动量比等。对水流交汇区水动力学特性的研究可以追溯到20世纪40年代,Taylor[1]最早采用动量方程对交汇角为45°和135°的明渠交汇水流进行理论研究,得到了上、下游水深比简单的关系式;Best[2]提出了有关交汇口附近流体的分区;Webber等[3]考虑了阻力的影响,通过保角映射的方法提出了水流交汇区的理论水流模式;Hsu等[4]根据试验结果得到水头损失系数以及和流量比有关的动量修正系数和动能修正系数的拟合表达式;茅泽育等[5-6]建立了考虑干、支流交汇角以及与流量比相关的动量修正系数和动能修正系数的一维数学模型,提出了动量损失系数的理论表达式;徐孝平等[7]将侧槽作为岸边排放口处理,运用水深平均k-ε流模式、刚盖假定及混合有限分析法,较好地模拟了直角交汇河段的流场特性;赵升伟等[8]针对明渠交汇口缓流流动特性,分别应用水深平均H-L模型及k-ε模型对明渠交汇区流动进行模拟,并应用实测资料对这2种模型进行验证比较;刘同宦等[9]应用三维多普勒流速仪(ADV)研究交汇角为90°时不同汇流比水流条件下交汇区域的三维水流结构及其脉动特性;冯镜洁等[10]以水槽试验为基础,结合数值模拟研究分析了交汇角为60°和90°时交汇区的特性;吴迪等[11-13]利用ADV对Y形交汇口水流的三维水力特性进行模型试验并进行数值分析。
基于水流交汇区浓度分布试验和理论研究,本文建立了适用于水流交汇区的水气两相流模型,模拟分析了不同交汇角、流量比以及动量比对交汇区水动力学特性的影响,研究了水流交汇区的水动力学特性。水动力学特性直接影响污染物浓度分布特征,研究可为交汇区污染物浓度扩散研究提供基础数据和参考,对排污口的位置选择以及河道治理等都具有重要的指导意义。
1 交汇区水气两相流数学模型的建立
1.1 模型方程
为模拟交汇区自由水面的水深变化,采用水气两相流三维紊流 k-ε模型,自由水面的确定采用VOF方法。定义函数αw和αa分别代表计算区域内水和气所占的体积分数,在每个单元中有 αw+αa=1。水气两相流的数学模型如下:

式中:ρ为流体密度,kg/m3;¯ui和¯uj分别为i和j方向上的时均速度,m/s;u′i和u′j分别为i和j方向上的脉动分量 ,m/s;¯p 为时均压力,Pa;¯gi为 i方向上的时均体积力,m/s2;υ为分子运动黏性系数,m2/s;υt为紊动黏性系数;k为紊动能;ε为紊动耗散率;σk和σε分别为k方程和ε方程的紊流Prandtl数,分别取值1.44和1.92;Gk为流速梯度引起的紊动能生成项;Cε1和 Cε2为经验系数,取值分别为 1.0和1.3;Cμ为经验系数,取值0.09;i,j=1,2,3,分别代表x,y,z这3个坐标方向。
1.2 边界条件
a.进口边界。进口边界条件按流量进口设置,给定水深、流量、紊动特征量k和ε。紊动特征量按式(5)~(6)确定:
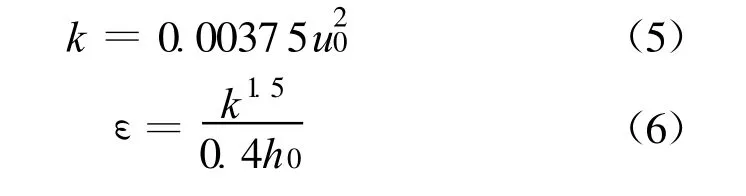
式中:u0为进口断面平均流速;h0为进口处水深。
b.出口边界。下游出流边界水位较稳定,流动是充分发展的,出口断面上的所有变量(压力除外)沿出口法线的梯度为零,表达式为

式中:n为出口断面的法线向量。
c.壁面边界。在近壁处采用标准壁面函数法得到近壁网格节点的变量值。引入无量纲参数 y+表示距离,设近壁点p到壁面的距离为yp,则
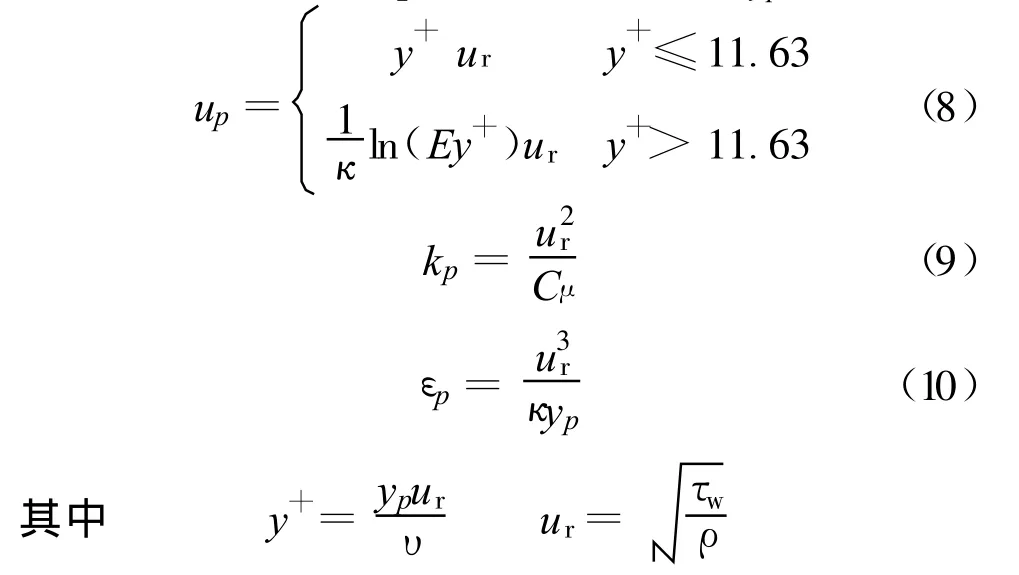
式中:up,kp,εp分别为p点的流速、紊动能和紊动耗散率;ur为壁面摩擦速度;τw为壁面切应力;κ和E为常数,分别取值0.42和9.8。
1.3 数值计算方法
采用有限体积法对通用方程在同位网格上进行离散,源项采用负坡线性化处理,动量方程离散时采用动量插值法,在计算界面流速时引入相邻两点的压力差。采用PISO[14]算法来求解压力、速度的耦合问题。
2 数学模型的验证
采用Weber等[15]的试验结果对本文建立的水气两相流数学模型进行验证。
2.1 Weber试验简介
Weber试验在交汇角为90°的等宽水槽中进行。干流水槽长21.95m,交汇口上游长5.49m,支流水槽长3.66m,主支流水槽宽度均为0.91m,高度为0.5m,水槽底部为平坡,干支流水槽上游各设有平流装置,试验水槽平面示意图如图1所示。
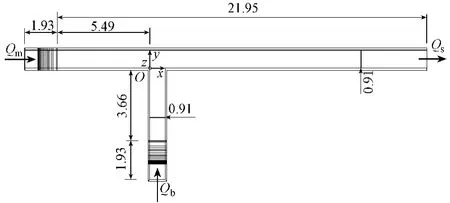
图1 试验水槽平面示意图(单位:m)
2.2 流场模拟结果的验证
数值模拟中坐标原点位于干支流边界交汇点上游,x轴方向为干流水槽的流动方向,y轴方向为支流水槽的流动方向,z轴方向为垂直向上方向,见图1。选取Weber试验中2组试验的测量结果对数学模型模拟结果进行验证,第1组的干流流量Q m和支流流量 Qb分别为0.071 m3/s和0.099 m3/s,第2组的Q m和 Q b分别为0.099 m3/s和0.071 m3/s。
图2和图3分别为第1组和第2组试验的自由水面高程计算值与试验值的对比。由图2和图3可知,水气两相流VOF模型模拟计算的自由水面高程与试验结果吻合较好,能够比较准确地模拟出交汇区的水面变化特征。
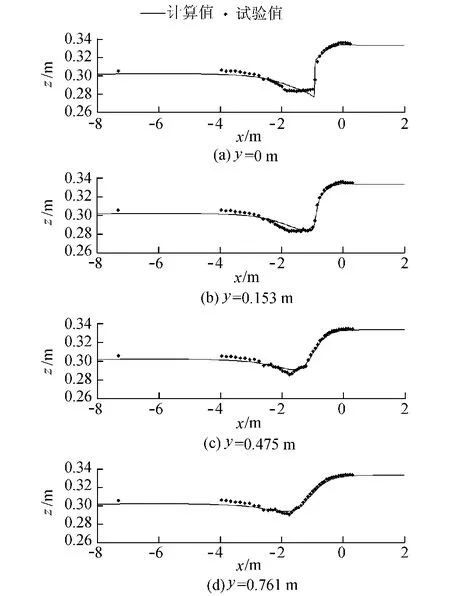
图2 第1组试验自由水面高程计算值与试验值的对比
图4为2组试验z=0.254m水平面的流线分布。从图4可以看出,支流汇入干流后,流线发生明显偏转,水流在交汇口下游交汇点处发生分离,流速减小甚至产生回流,形成分离区。图5为第2组试验z=0.254 m水平面的流速分布数值模拟结果与试验结果的对比。从图5可以看出,流速分布数值模拟结果与试验结果接近,但数值模拟结果比试验结果略小。
图6为第2组试验 x=2.132m横断面流速分布的数值模拟结果与试验结果的对比。从图6可以看出,水气两相流模型模拟得到的二次流与试验结果趋势相似,但速度值及环流中心位置存在一定的差异。分析其原因:在水流交汇区流动中,除了由于弯道流动特征引起的第一类二次流外,同时存在由各向异性紊动引起的第二类二次流,而k-ε模型本身的各向同性假定导致二次流模拟结果存在一定误差。
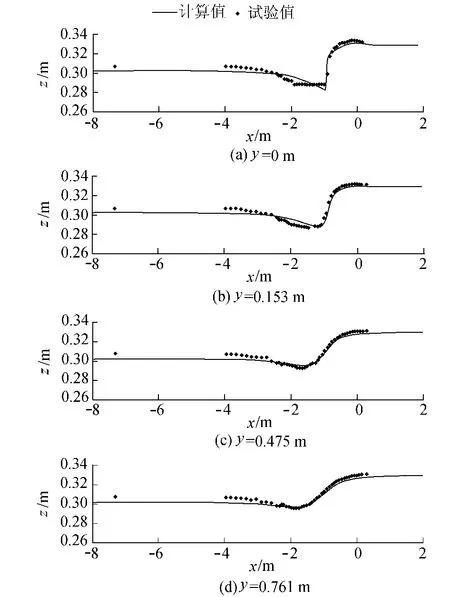
图3 第2组试验自由水面高程计算值与试验值的对比
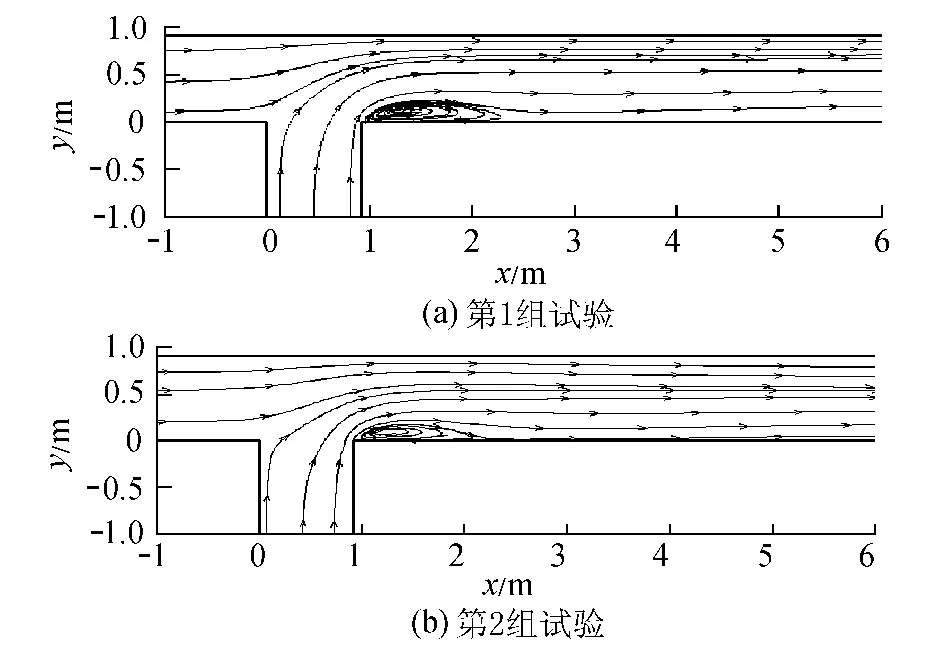
图4 2组试验z=0.254m水平面的流线分布
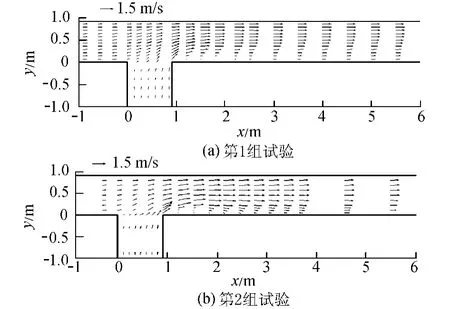
图5 第2组试验z=0.254m水平面流速分布数值模拟结果与试验结果的对比
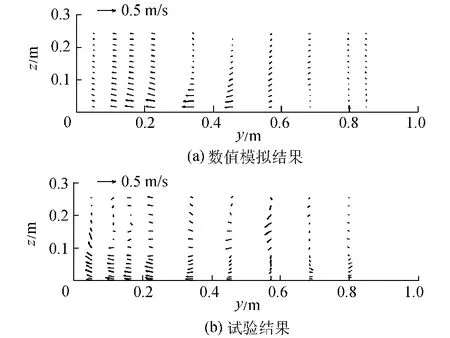
图6 第2组试验x=2.132m横断面流速分布的数值模拟结果与试验结果的对比
3 交汇区水动力学特征的数值模拟
3.1 计算模型及工况设置
采用水气两相流数学模型对不同交汇角、流量比和动量比开展数值模拟研究。数值计算模型参考Weber试验水槽,模型大小略有变化,其中干流长27 m,交汇口上游长6m,支流长6m,主支流宽度均为1 m,高度为0.6 m,底部为平坡,坐标原点位于干支流边界交汇点下游。
数值模拟工况见表1,每组工况交汇口下游总流量 Q s均为0.12m3/s。
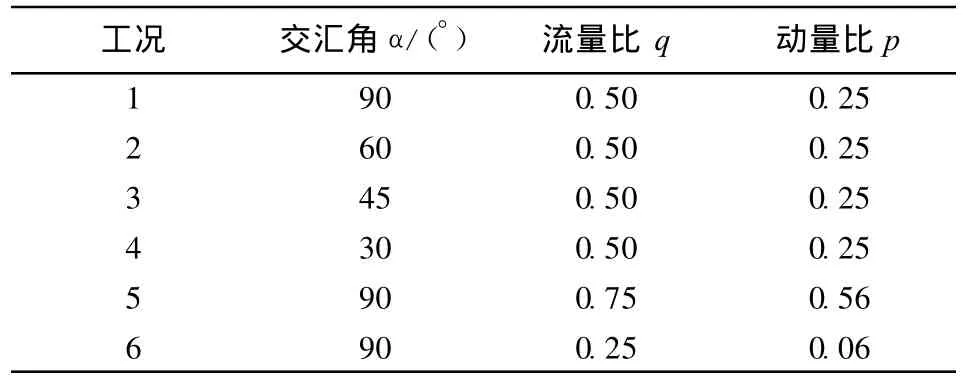
表1 数值模拟工况
3.2 网格划分
不同交汇角网格划分的原则基本一致,即对交汇口附近的区域网格加密,而交汇口向上游和下游方向网格均逐渐稀疏;在垂向和横向考虑边壁的影响,对底部及边壁处加密;为了精确求解自由水面位置,对水气两相交界区域的网格加密。以交汇角为90°时的模型为例,网格单元总数为 26.96万个,最小网格体积为 5×10-6m3,最大网格体积为3.8×10-4m3。
3.3 交汇角对流场特征的影响
图7为不同交汇角时的水位分布比较。从图7可以看出,在流量比和动量比相同的情况下,交汇角越小,交汇口上游的壅水现象越不明显,上、下游水位差越小,分离区内的水位下降程度及分离区的范围也越小。
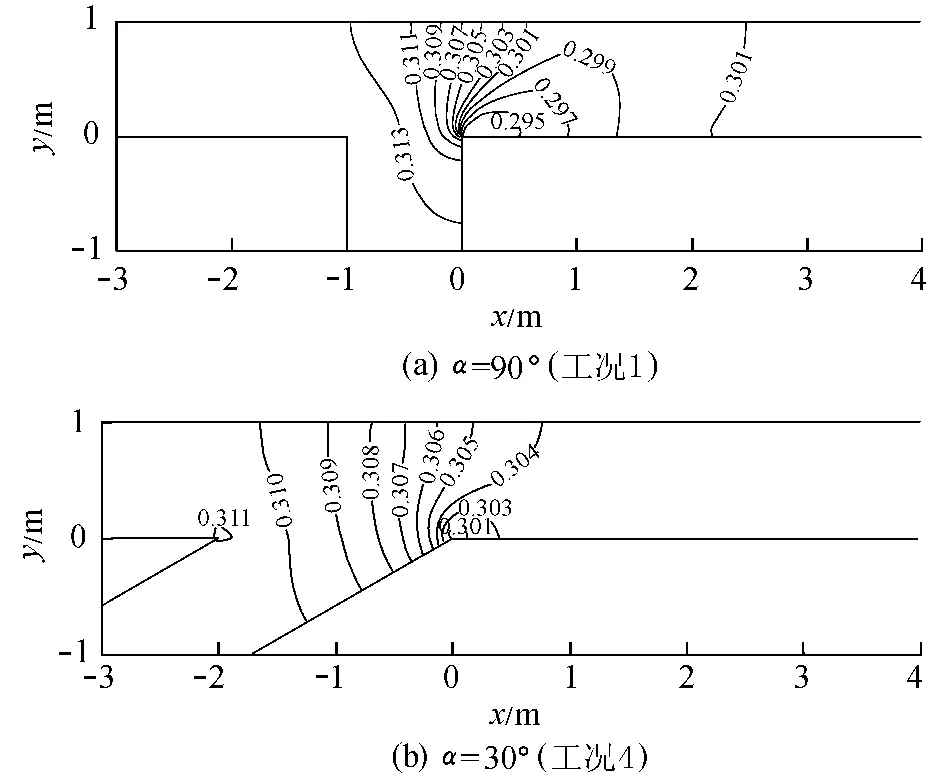
图7 不同交汇角时的水位分布比较(单位:m)
图8为不同交汇角时z=0.250m水平面流线分布比较。从图8可以看出,在流量比和动量比相同的情况下,交汇角越小,支流对干流的干扰越小。交汇角的大小对分离区的出现及形状影响较大。随着交汇角的减小,支流流线在交汇口下游的偏转程度逐渐变小,分离区的范围逐渐缩小直至完全消失。在交汇角为45°时,没有回流现象发生,而在交汇角为30°时,分离区已经完全消失,仅在交汇口下游存在流线弯曲现象。
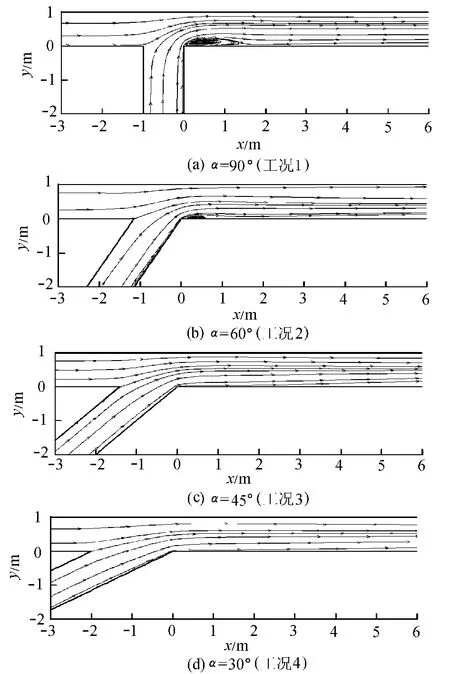
图8 不同交汇角时z=0.250m水平面流线分布比较
3.4 流量比和动量比对流场特征的影响
图9为不同流量比和动量比时的水位分布比较。从图9可以看出,在交汇角一定的情况下,流量比和动量比越小,上游的壅水现象越不明显,上、下游水位差越小,分离区内的水位下降程度及分离区的范围也越小。
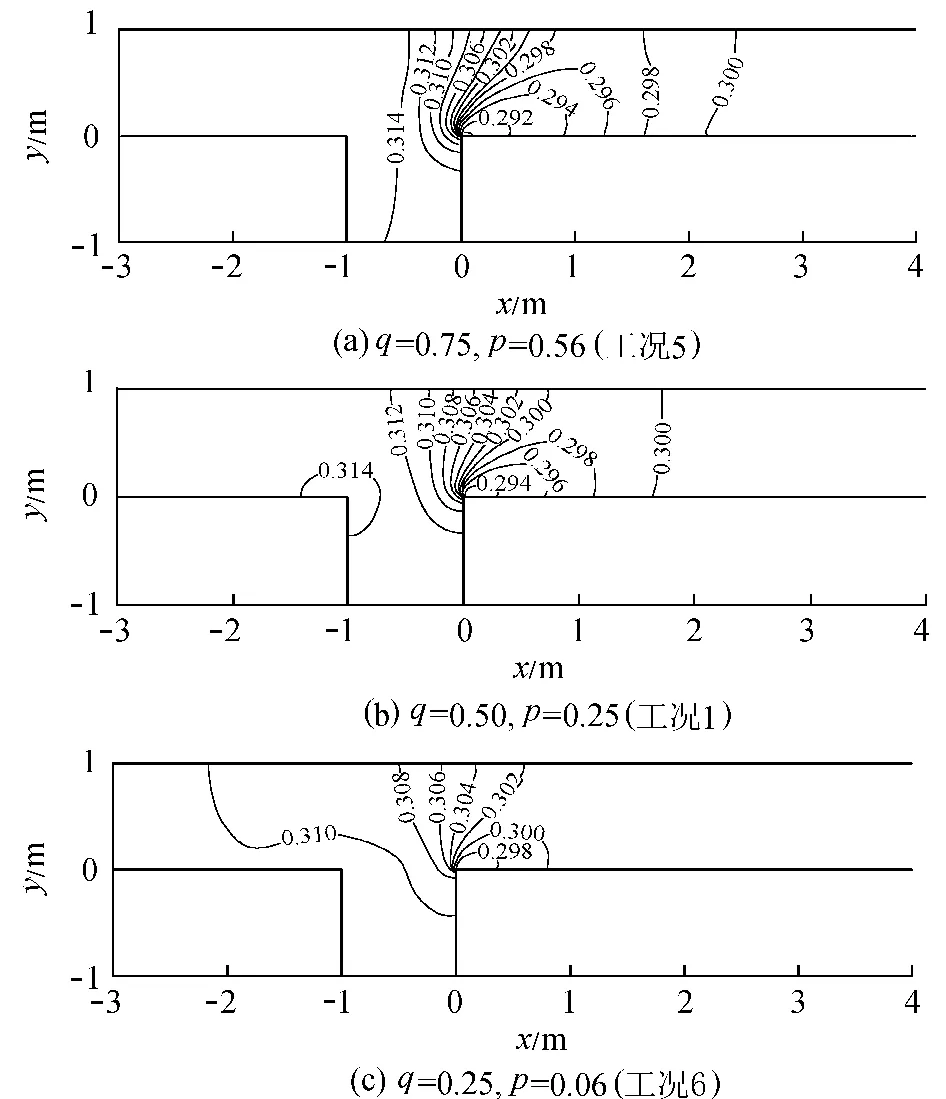
图9 不同流量比和动量比时的水位分布(单位:m)
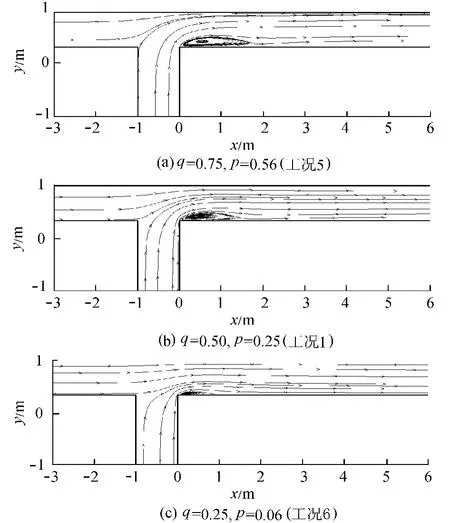
图10 不同流量比和动量比时z=0.250m水平面流线分布比较
图10为不同流量比和动量比时z=0.250m水平面流线分布比较。从图10可以看出,在交汇角一定的情况下,不同流量比和动量比工况下形成的分离区形状相似,随着支流、干流的流量比和动量比减小,支流对干流的干扰程度逐渐降低,形成的分离区形状和尺寸逐渐变小。
4 结 语
本文建立的水气两相流模型较好地模拟了交汇区的自由水面和流场内部特征。数值模拟研究结果表明:交汇角、流量比和动量比越小,支流对干流的干扰越小,交汇口上游水位的壅高及分离区内水位下降程度越不明显;在流量比和动量比一定的情况下,随着交汇角的减小,分离区的范围逐渐缩小直至分离区消失;在交汇角一定的情况下,随着流量比和动量比的减小,分离区的形状和尺寸逐渐变小。
水体的水动力学条件是污染物迁移、转化的基本背景条件。本文开展的水流交汇区水动力学特性研究,可以为水流交汇区污染物浓度扩散研究提供基础数据和参考,但由于水流交汇区水流结构的复杂性与数值模拟本身的局限性,本文建立的水气两相流数学模型尚不够完善,水气两相流模拟结果与实际情况存在一定的差异,因此对本文数学模型进行更广泛的验证和完善是今后值得进一步研究的问题。
[1]TAYLOR J L.Flow characteristics at rectangular open-channel junctions[J].Trans,1944,109:893-902.
[2]BEST J L.Flow dynamics at river channel confluences:implications for sediment transport and bed morphology[C]//Recent Developments in Dluvial Sedimentology.Tulsa:Society of Economic Paleontologists and Mineralogists,1987.
[3]WEBBER N B,GREATED C A.An investigation of flow behavior at the junction of rectangle channels[J].Proc Inst Engrs,1966,34(8):321-334.
[3]WEBBER N B,GREATED C A.An investigation of flow behavior at the junction of rectangle channels[J].Proc Inst Engrs,1966,34(8):321-334.
[4]HSU C C,WU F J,LEE W J.Flow at 90°equal-witdth open channel junction[J].Journal of Hydraulic Engineering,1998,124(2):186-191.
[5]茅泽育,罗旰,赵升伟,等.等宽明渠交汇口水流一维数学模型[J].水利学报,2004,35(8):26-32.
[6]茅泽育,赵升伟,罗旰,等.明渠交汇口水流分离区研究[J].水科学进展,2005,16(1):7-13.
[7]徐孝平,彭文启,李炜.直角交汇河段流场特性分析[J].水利学报,1993,24(2):22-31.
[8]赵升伟,茅泽育,罗旰,等.等宽明渠交汇水流数值计算[J].河海大学学报:自然科学版,2005,33(5):494-499.
[9]刘同宦,郭炜.主支汇流比对交汇区域水流脉动特性影响试验[J].水利水电科技进展,2009,29(3):6-9.
[10]冯镜洁,李然,王协康,等.河流交汇分离区特性研究[J].水动力学研究与进展:A辑,2009,24(3):321-325.
[11]吴迪,郭维东,刘卓也.复式断面河道“Y”型交汇河口水流水力特性[J].水利水电科技进展,2007,27(3):21-23.
[12]郭维东,梁岳,冯亚辉,等.Y型明渠交汇水流分离区的数值分析[J].水利水电科技进展,2007,27(6):50-52.
[13]郭维东,王晓刚,曹继文,等.“Y”型汇流口水流水力特性试验研究[J].水电能源科学,2005,23(3):53-56.
[14]王福军.计算流体动力学分析:CFD软件原理与应用[M].北京:清华大学出版社,2004:87-91.
[15]WEBER L J,SCHUMATE E D,MAWER N.Experiments on flow at a 90°open-channel junction[J].Journal of Hydraulic Engineering,2001,127(5):340-350.

