简论数学认知与语言认知差异性及其启示

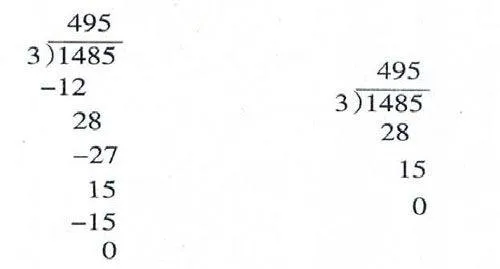
一、前言

根据万方数据知识服务平台知识脉络分析，数学认知的研究从2004年到2009年6年间从研究的高峰几乎进入目前的停滞状态，与此相反，语言认知却在节节攀升，2010年达到最高，并且上升势头强劲。而数学语言本身就是从自然语言中分离出来的，美国著名心理学家布龙菲尔德说：“数学不过是语言所能达到的最高境界”。更有苏联数学教育家斯托利亚尔言：“数学教学也就是数学语言的教学”。因此，要研究究竟是什么原因导致数学对英语学习者而言如此的困难这一课题，必须要将二者紧密结合起来。对于外语教学而言，语言认知能力在数学认知能力发展中究竟起着一个什么样的作用也是一个亟待回答的问题。针对这一问题，下面将就数学认知与语言认知的差异性及其启示作相关性论述。

二、数学认知与语言认知的差异性

首先，英语学习者必须过滤数学知识——语言本身存在的问题——通过第二外语过滤。这样一来，数学事实上就成了他们的“第三”语言。社会语言符号的随机性、冗余性、离散性、递归性以及层次性和数学语言的抽象性、精确性之间的跨越对大多数语言学习者而言是一个不小的跨越，这种过滤的转化要求较强的逻辑思辨能力才能完成。数学认知和语言认知的概念内涵不同，信息传递方式不同，构造方式不同，结构完备性不同，内容的科学性不同也为纯语言学习者制造了不小的认知障碍。

其次，数学学习是有连带关系的。比如，学生要学会乘除以前必须学会加减，必须学会了乘除，才可能学会比率。并且，学生学习数学的过程中，内容和教材越来越复杂。因此，当语言学习者进入到高一年级时，他们面对了越来越大的挑战，跟进度或跟上同学。结果，这样的差距就被扩大了[1]。

第三，数学词汇在日常生活中并不常用，本身属专业术语范畴，定义很局限。Krussel认为，语言是数学建构中最基本的组成部分，因为语言是数学不可割裂的工具。这样一来，语言学习者无法成功解决具有复杂而陌生的专业词汇的问题就不足为奇了。对于这些只学习英语语言的学生，“最小公分母”、“比率”、“商数”意义不多。绝大多数情况下，这些概念是新的，或者说，这样的词汇使用完全有别于他们所学习的普通语言。

第四，数学中使用的句法语言结构异常复杂并非常特别。许多第二语言学习者认为数学中出现的句法累赘呆板。比如，比较用法，高、大，一样多；被动语态的，X加以Y；陈述已知和未知的逆向思维法，如X比Y少2（正确的等式是X=Y-2，而不是X-2=Y）加重了这种迷惑性。它和一般的文学描述语言不同，这些语言更加精炼，这使得第二语言学习者更加难以理解。一个9年级的双语学习者在算数课堂上看到这样的表达式“X3>N”，解释说是“我口袋里的5分镍币数是1毛镍币的3倍”。有专家将这个错误的反应归结于用词中的语言对等错失。因此，这个学生误释“超过”为不等的陈述。

第五，第二语言学习者的阅读技能影响了他们的数学表现。以前的研究也表明数学和阅读成绩之间具有很强的关联性。McGhan在对密歇根州139个学校4年级学生阅读理解能力和数学测验成绩调查后发现，它们之间的关联度高达84个点。除了数学词汇和表达方式的难度外，第二语言学习者处理信息能力比他们的同学相对来说要慢，主要原因在于他们阅读速度很慢。

第六，Chamot and O'Malley的研究结果表明，数学程式受限于文化，不同的文化使用不同的方法解决问题，或者他们用的征象都不一样。中美之间使用的除法分解式就很不一样。如下图：

（美国使用的长除法） （中国使用的简捷除法）

甚至就是读数的方法也因文化而差异巨大。比如200，000，中国读作：二十万，韩国却是20个man，即“twenty ten thousand.”（读作as m-ah-ri），而英语读作：“two hundred thousand”。

第七，不仅数学问题在以一种文化差异的方式解决，数学问题也在受着社会文化的约束。Solano-FIores and Trumbull研究中就发现这样的情况，一个句子“[Sam's] mother has only $ 1.00 bills”，第二外语学习者也误读单词“only”，将这个句子理解为“珊姆的妈妈只有一元钱”。这样的误译很有可能与社会经济身份有关，来自低收入家庭背景的孩子可能有更多的“维持生计”观点，从而把他们的关注映射到了问题的理解上。

第八，除了因文化迥异导致解决问题的方式具有较大差异性外，如果学生不熟悉主流社会文化环境或对文化信息想当然理解，也不能完全解决数学的用语问题。例如，第二外语学习者可能无法理解Mardi Gras parade（同性恋大游行），从而引发语言及环境的理解性障碍。

三、启示

基于以上探讨，我们不难理解为什么第二外语学习者认为数学具有很大挑战性。更有甚者，许多教师也误以为数学与语言无关，而且仅仅是一些表征和数字。这样，他们就觉得，这些学生应该在数学课堂上接受挑战。这确实有待进一步探讨。Abedi研究发现，第二外语学习者和母语学习者之间在计算数学中差距甚微。事实上，许多研究（Abedi，2004；Abedi，Hofstetter， Lord，2004；Abedi Lord，2001；Brenner，1998；Khisty，1997；Olivares，1996；Solano-Flores Trumbull，2003）都表明外语学习者在术语问题和解决数学问题方面远远落后于母语习得者，主要的原因就在于他们外语水平有限。研究结果表明，第二外语学习者和母语习得者在分析数学成绩方面的差异远大于在计算数学方面，因为前者包含有更多的复杂语言表达式，就后者而言，确实差距不大。第二外语学习者在解决数学问题方面的较差表现应该是因为他们的语言水平不高所致，这也影响了他们学习数学知识。虽然他们能跟上低水平的数学机制和许多测试，但他们仅能做简单的计算。在文化方面的成绩评估中，第二语言学习者面临着越来越严酷的挑战。

语言学习和数学学习的认知大脑机制还有待研究者做进一步的调查。如，Sandrini，Miozzo，Cotelli， Cappa对一位因事故造成脑损伤的病人，该被试听力理解受到中度损害，而且被试患有严重的朗读失能症和书写失能症。对被试进行算术认知能力测试时，发现她的算术认知能力受到的损害具有选择性特点。语言认知能力在数学认知能力发展中的作用似乎在减弱，但通过语言认知能力培养探索数学认知能力提高的路径绝非海市蜃楼，相反，笔者认为，回到原点，才可能找到真正的有效方案。

参考文献

[1] Adams，T.L.（2000）.Helping children learn mathematics through multiple intelligences and standards for school mathematics.Childhood Education，77（2），86-92.

[2] Aram，D.M. Nation，J.E.（1980）.Preschool language disorders and subsequent language and academic difficulties.Journal of Communication Disorders，13，159-170.

[3] Balow，I.H.（1993）.Metropolitan Achievement Test Primary.Orlando，FL：HarcourtBrace，Inc.

[4] 陈英和，耿柳娜.儿童数学认知策略研究新进展.北京师范大学学报（社会科学版），2003（1）.

[5] 曹才翰，蔡金法.数学教育学概论.南京：江苏教育出版社，1989.

[6] 张庆林.当代认知心理学在教学中的应用.重庆：西南师范大学出版社，1995.

（责任编辑 陈国庆）