基于折叠方法的数据压缩方法实现

范海波

摘要:该文提出了一种基于折叠关系压缩方案，该方案是利用折叠技术,将SOC芯片中芯核的测试数据整体进行折叠关系的判断,并且能够根据是否存在折叠关系把原测试数据分为两段,在此基础之上并分别对有折叠关系的测试数据进行折叠压缩，对没有折叠关系的测试数据使用相容压缩。目前，减少测试应用时间和测试数据容量是测试领域的努力方向。该文提出的这种方法可以有效的减少存储容量和降低测试时间从而有效的降低了测试成本。与类似的纯编码压缩方法相比，如：Golomb码，统计码，基于字典的编码等压缩方法，其压缩效果更为显著。

关键词：内建自测试；折叠计数器；测试数据压缩；相容压缩

中图分类号：TP311文献标识码：A文章编号：1009-3044(2012)15-3494-03

Data Compression Method Realization Based on the Folding Method

FAN Hai-bo

（Anhui Nari Jiyuan Software CO.,LTD., Hefei 230088, China）

Abstract：In this paper, a relationship based on folding compression programme, which is to use folding technology, SMIC chip SOC nu clear test data to the overall collapse of relations between the judgement and can collapse under the existence of relations between the origi nal test data is divided into two sections, On this basis and were to have folded the fold test data compression, in order to obtain a higher compression ratio, the collapse did not use the compatibility test data compression. At present, to reduce test application time and test data capacity is to test the field of direction. The proposed this approach can effectively reduce the storage capacity and reduced testing time, thus effectively reducing the cost of test. And a similar-encoding method, such as: Golomb code, code statistics, based on the coding dic tionaries, such as compression method, the compression effect more significant.

Key words: BIST(built-inself-test);folding counter;testing data compression;compatible compression

隨着芯片集成度的提高，大量的知识产权（IP）核被用于系统芯片（SOC）的设计，这导致了测试数据量和测试时间的快速增加，以及测试芯核难以进入。它使得传统的离线测试越来越不适应IC的发展。

最近提出的一些有效的压缩和解压方法主要有以下几类：一类是将预先计算的测试集TD分成固定长度的b位块，将这些定长位块作为研究的对象。例如，统计码就是统计这些定长位块在测试集中出现的频率，并用哈夫曼码编码这些定长位块。考虑到长度为b的位块可能出现的组合情况有2种，若用全哈夫曼码进行编码，码树庞大，相应的硬件开销就会非常巨大，所以统计码（又称有选择的哈夫曼码）仅对频率出现最高的几个位块进行编码，用小于b位的码字代替它们，其余块不变。另一类方法是用特征位的长度代替特征位本身，通过对长度值进行编码来达到压缩的目的。这种方法基于对测试集特征的观察，即测试集的测试模式之间不同位（变化位）较少，通过测试模式之间的异或运算，形成一个差分向量序列，序列中的连续“0”很多，通过编码连续“0”序列的长度，可以有效地压缩测试数据，在解压时，使用一个循环扫描移位寄存器（CSR）就可以还原出原测试集。

1相容压缩技术

1.1相容技术的理论背景

相容压缩技术是一种使用广泛的数据压缩技术，它是利用数据间的相容关系进行数据的压缩。所谓相容关系，指的是当两个向量是相容的当且仅当对任意位置，两个向量中的对应位是相同的或者至少有一个为无关位。

1.2完整的综合过程

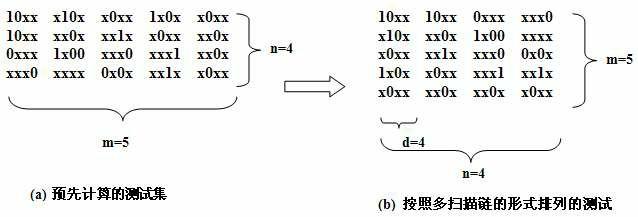
在本文中，把测试结合转化为多扫描链的形式是做相容压缩的前提。通过识别相容扫描链来减少存储的测试数据量，这些扫描链对其他扫描链来讲，能够提供相似信息或测试数据的线形结合。通过相容压缩一方面可以减少测试数据量，提高压缩率；另一方面相容压缩可以减少测试向量的宽度，从而减少了所需的循环移位扫描寄存器（CSR）的长度。而在相容压缩前，首先需要把测试集按照多扫描链的形式进行排列。例如，预先计算的测试集Td是由n个测试模式t1,t2,t3,…,tn组成，被测电路的扫描单元被分为m条扫描链（0,1,2,…,m-1）,那么每个测试模式被分成m个子向量，且每个子向量的长度相同，记为d，在长度不足d的子向量的尾部填充无关位，且在测试向量转化后不足m条扫描链时，在剩余的扫描链上用无关位填充（即当width % m>d，width为测试向量的宽度）。

如图1，其中，测试向量的宽度width=20,测试模式个数即行数n=4,取扫描链的条数m=5,那么子向量的长度d=4。(x表示无关位)

图1将原始测试集转化为多扫描链形式

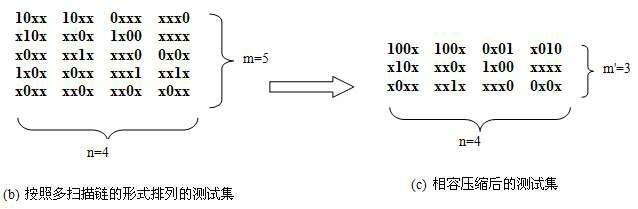
图1中，第0行，第3行和第4行是相容的，所以可以合并成一个向量，第1行，第2行无与之相容的，故单独作为一个向量，不合并，由此可以得到相容压缩后的测试集。最终实现了多扫描链的相容压缩。

因此，由图2得知，通过基于多扫描链的结构的第一次的相容压缩，测试集的无关位减少了，也就是减少测试数据量和移入扫描链的时间，提高了压缩效率和降低了测试成本。同时，相容压缩也减少了测试向量的宽度，从而减小了CSR的长度。而对相容压缩这部分的解压，只需要通过从合并项中引入几条扇出线就可以实现了，解压的硬件非常简单，使得软硬件开销达到最小。这是第一次压缩的重要意义所在，为以后的测试数据压缩方法提供了一种新的思想。

图2将排列后的测试集进行相容压缩

2基于折叠关系的数据压缩方案

2.1折叠技术的基本思想

根据上述理论知识可以将算法分解成异或运算、折叠关系判断、一致性判断、生成折叠关系集合、生成种子并根据折叠关系段分测试集合。根据分析可以看出要达到理想的压缩效率生成尽量少的种子，以这些种子来翻转后生成的向量集合可以含盖原来的测试集合，而要达到这个目的关键是要找到一个最大的折叠集合，而找到最大的折叠集合的关键是找到一个与尽量多的向量有相同的折叠距离的向量e。要找到使得生成种子数目最少的向量e的算法比较难，在这里我采用了一种没有经过优化的简单算法来实现折叠种子的生成。

首先每次选取还没有被处理的向量集合中的第一个向量作为向量e，然后从1到n循环的选取折叠距离，每选取一个折叠距离将e与所有剩下的向量进行异或运算，再对运算结果进行判断以此来确定e与相应的向量是不是有折叠关系。就记录下与他折叠关系的向量和向量的个数，循环结束后就进行判断，当折叠距离为几时向量e所包含的折叠集合的数目最多，并选取这个折叠距离和相应的折叠集合，然后通过一致性判断将折叠集合中有冲突的向量剔除出去。最后根据向量e和相应的折叠距离来生成这个折叠集的折叠种子。

2.2相容技术的基本思想

通过上面对折叠技术思想的分析可以看出，在对一个测试集合进行折叠种子生成时，不是每一个测试向量都存在与之有折叠关系的向量的，也就是说，如果一个测试集合中的所有测试子集合都不彼此都不存在折叠关系，那么通过折叠压缩生成的种子集合会接近测试集合本身的大小，所以，在生成测试集合折叠种子的过程中，可以考虑通过折叠算法将原测试集合分为两个部分，既具有折叠关系的测试集合和不具有折叠关系的集合分开放置，在对具有折叠关系的集合进行折叠压缩，不具备折叠关系的测试集合采用其他方式压缩，这样就会在折叠压缩的理论基础上更进一步的减少种子的位数，达到提高压缩率的目的。

在这里，使用基于多扫描链的相容关系来对相互之间不具备折叠关系的测试集合进行相容压缩，已达到更高的压缩率。

2.3方案的总体流程

综合上面分析过程，为了得到更高的压缩效率。可以将测试数据当作一个测试集合，用折叠种子生成算法来生成相应的折叠种子。在第二步生成折叠种子的过程中，记录存在折叠关系的测试集的序号以及不存在折叠关系的测试集合的序号。这一点对提高压缩效率是至关重要的，因为对没有折叠关系的测试向量使用折叠压缩是不能得到理想的压缩率的。但对于存在折叠关系的测试向量使用折叠压缩要比使用其他压缩方法要好的多。所以根据折叠关系的存在与否将测试向量分为两段，以保证可以得到更好的压缩效果。第三步，根据第二步所得到的两段测试向量，分别进行相宜的压缩，并记录压缩率。

3实验结果与分析

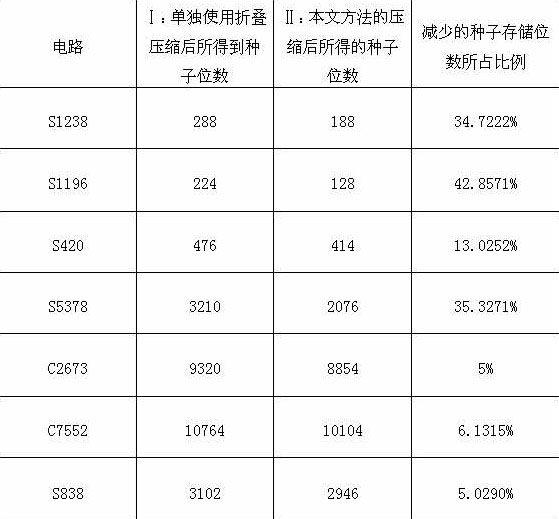
在本文建议方案中，我们先通过存储折叠距离来控制确定的测试模式生成，表1给出了全部通过折叠压缩来生成测试种子方案和本文中采取折叠压缩有折叠关系的测试向量和相容压缩(取扫描链长度为50)时各自需要存储的种子的位数，以及使用本文方法所减少的种子存储比例。

表1減少的存储位数

由表中可见，采用本文中使用的方法对于大部分的测试集合都可以减少生成种子的存储量，也证明这中方法是有效果的。

4总结与展望

本文提出了基于折叠关系的数据压缩的实现方法。通过折叠关系将原测试集合划分为两段，分别对每段使用合适的压缩方法，以达到更好的压缩效果，同时我还发现在实现压缩的时候，可以根据折叠关系的特点降低功耗，并且根据测试集合的大小选择合适的扫描链的长度来近一步提高书记压缩率，这些方法在理论上是可以实现的，目前，我正基于这两个方面对程序做进一步的改进，希望可以得到更高的压缩率，减少更多的压缩时间。

下面是我对降低功耗的一些设想：降低功耗我们采取了以下两种措施，

1）我们先删除冗余向量，使得这些冗余向量不需要被生成，测试，因此可降低功耗。

2）再对折叠计数器序列生成次序加以控制，使所需的翻转次数减少,从而降低功耗。

参考文献：

[1]梁华国, Hellebrand S,Wunderlich H J.一种基于折叠计数器重新播种的确定自测试方案[J].计算机研究与发展,2001,38(8).

[2]梁华国，蒋翠云.使用双重种子压缩的混合模式自测试[J].计算机研究与发展,2004,41(1).

[3] Abramovici M,Breuer M,Friedman A.Digital Systems testing and Testable Design[M].New York:Computer Science Press,1990.

[4] Hellebrand S,Rajski J,Tarnick S,et,al.Built-in Test for Circuits with scan Based on Reseeding of Multiple-Polynomial Linear Feedback Shift Registers[J].IEEE Trans. On Comp.,1995,44(2).