边缘检测优化算子在轮胎痕迹识别中的应用
张汉欣
(中国刑事警察学院 辽宁 沈阳 110854)
边缘检测优化算子在轮胎痕迹识别中的应用
张汉欣
(中国刑事警察学院 辽宁 沈阳 110854)
本文以快速准确识别轮胎痕迹为目的,针对道路交通事故现场轮胎痕迹图像,主要应用了Sobel算子、Roberts算子、Prewitt算子、Laplacian算子、马尔算子(Log)算子和Canny算子等算法对轮胎图像痕迹边缘识别。根据传统的多种优化算子的图像处理算法比较,实验结果表明,Canny算子算法处理的图像空稀少,内容丰富,轮胎花纹边缘清晰。
轮胎痕迹 识别 边缘检测 优化算子
1 引言
常用的、最简单的边缘检测方法是对原始图像按像素的某邻域构造边缘检测算子,检验图像的每个像素在某个邻域内灰度的变化,利用边缘邻近一阶或二阶方向导数变化规律来实现检测。由于原始图像一般含有噪声,而边缘和噪声在空间域反应为灰度有幅度起伏,在频域表现为高频分量,这就给边缘检测带来困难。传统的边缘提取方法是边缘的种类可分为两类:一类称为阶跃性边缘,它两边像素的灰度值有着显著的不同;另一类称为屋顶状边缘和凸缘边缘,它位于灰度值从增加到减少的变化转折点。对于阶跃性边缘,二阶方向导数在边缘处呈零交叉;而对于屋顶状边缘和凸缘边缘,二阶方向导数在边缘处取极值。由于利用一阶导数进行边缘检测时,如果所求的一阶导数高于某一闭值,则可确定该点为边缘点。这样就会导致检测的边缘点太多。而利用一阶导数的局部最大值对应的二阶导数的零交叉点能够找到精确边缘点。优化的边缘检测应当准确解决边缘的虚实、交接、棱边等问题。
边缘检测算法目前多集中在对灰度图像的处理,通过构造对像素灰度级阶跃变化敏感的微分算子,例如梯度算子,其边缘检测速度快,但得到的常是不连续的、不完整的结构信息。这类方法对噪声较为敏感。为了有效抑制噪声,一般都先对原图像进行平滑,再进行边缘检测就能成功地检测到真正的边缘。本文应用的边缘检测算子有索伯尔(Sobel) 算子、罗伯特(Roberts)算子、普瑞威特(Prewitt)算子、拉普拉斯(Laplacian) 算子,马尔(Log) 算子及Canny算子等。
2 梯度算子
一幅数字图像一般是图像灰度连续函数的离散化取样点数组,图像灰度值的明显变化可用梯度的离散逼近函数来识别。
索伯尔算子的表达式为:

索伯尔(Sobel) 算子属于梯度算子的一种,具有两个突出的优点:一是由于引入了平均因素,对图像中的随机噪声具有一定的平滑作用;二是由于它是相隔两行或两列的差分,因此边缘两侧的元素得到加强,使边缘显得粗而亮。
罗伯特算子的表达式为:
max{|f(i,j)-f(i-1,j-1)|+|f(i-1,j)-f(i,j-1)|}
罗伯特(Roberts)算子对于陡峭的低噪声图像具有最良好的响应,利用局部差分算子寻找边缘算子。
普瑞威特算子的表达式为:

普瑞威特(Prewitt)算子与索伯尔算子的区别仅是模板不同、其原理相同且效果相当;与罗伯特算子又类似。
上述三种算子都属于梯度算子。梯度的大小代表图像边缘的强度,梯度方向与图像边缘幅度走向垂直。由于梯度算子仅计算相邻象素的灰度差,对噪声敏感,难以抑制噪声的影响。由此还演变出方向算子,但增多的模板使计算趋于复杂。
3 马尔算子
如果在计算一阶导数求梯度的方法中把大于某值的点取为边界点,就会出现检测出的边缘点繁多现象,则在理论上更有效的方法是求梯度局部最大值对应的点,将其确认为真实边缘点。这样消除了一阶导数中的非局部最大值,可检测出更准确的边缘。一阶导数的局部最大值对应着二阶导数的零交叉点。通过确定图像灰度的二阶导数的零交叉点就可确定真是的边缘点。
对于阶跃状边缘,其二阶导数在边缘点就有零交叉,并且边缘点两旁象素的二阶导数不同号。这样对数字图像的每个像素计算关于X、Y两轴的二阶偏导数之和,就可得拉普拉斯(Laplacian)算子。拉普拉斯算子表达式为:
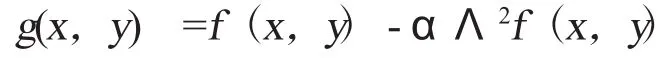

已知拉普拉斯算子是满足二维图像不同走向的轮廓锐化要求。由于梯度算子在利用图像灰度二阶导数的零交叉点来求边缘点的算法对噪声相当敏感,拉普拉斯算子一般不以其原始形式用于边缘检测,希望在边缘增强之前去噪,即图像进行高斯滤波平滑处理。Marr和Ildreth将高斯滤波和拉普拉斯边缘检测结合在一起,形成马尔算子,通常被称为Log—Laplacian of Gaussian算子。该方法先对图像进行平滑处理,即是利用高斯函数平滑图像后,用拉普拉斯(Laplace)算子检测边缘,从而降低了图像的噪声。这一算法称为高斯拉普拉斯(Log)算法,马尔算子的近似5×5模板及检测效果。
其中:*为卷积,r2=x2+y2,r是离中心点的径向距离;▽2h为高斯拉普拉斯滤波算子,是轴对称函数,且各向同性。
函数在r=±σ处有过零点,在|r|<σ时取正值,在|r|>σ时取负值。且算子在定义域内的平均值为零,因此将它与图像卷积并不会改变图像的整体动态范围,但由于它相当光滑,所以卷积结果使图像变得模糊,其模糊程度正比于σ。
马尔方法的特点是图像先与高斯滤波器进行卷积,这样在平滑了图像的同时可以去噪,孤立的点噪声和较小的结构组织将被消除。由于平滑导致边缘的延展,因此边缘检测只考虑那些具体局部梯度最大值的点为边缘点。
4 Canny算子
Canny边缘检测算子是John.F.Canny于 1986年开发出来的一个多级边缘检测算法。Canny创立了边缘检测计算理论 (Computational theory of edge detection)。Canny算子(或者这个算子的变体)是最常用的边缘检测方法。在Canny创造性的工作中,他研究设计了一个用于边缘检测最优平滑滤波器,这个滤波器能够很好地被一阶高斯导数优化。另外,Canny引入了非最大抑制概念,它是说边缘定义为在梯度方向具有最大梯度值的点。
Canny算子应满足的信噪比准则是不丢失重要的边缘,不出现虚假的边缘,表达式为:

其中:f(x)是边界滤波器的脉冲响应;G(x)是边缘;n0是高斯噪声的均方根。
Canny算子满足定位精度准则,即真实边缘与别的边缘位置之间的误差最小,即
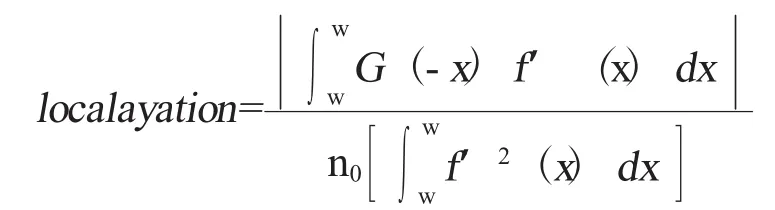
其中G′(-x)和f′(x)分别是G(-x)和f(x)的一阶导数。
Canny算子应满足的单边缘响应准则是在有噪声的情况下,边缘附近会有多个过零点。两个检测到的过零点的平均距离为
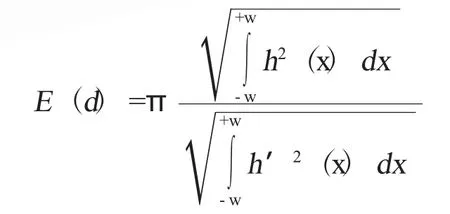
平均距离越大,过零点间距越大,越容易检测。
Canny算子实现的具体步骤如下:
(1)对原始数据用二维高斯滤波模板进行卷积,得到的图像与原始图像相比有些轻微的模糊(blurred)。这样,单独的一个像素噪声在经过高斯平滑的图像上变得几乎没有;
(2)利用微分算子(如普瑞威特算子、索伯尔算子等)找到图像灰度沿着两个方向的导数Gx,Gy,并求出梯度的大小:
(3)利用梯度大小计算出梯度的方向,求出边缘的方向,就可把边缘的梯度方向大致分为4种(水平、垂直、对角线方向45度和135度)方向的边缘,将原始图像与每个所作的卷积都保存起来,对于每个点都确定在这个点上的最大值以及生成的边缘的方向,这样就从原始图像生成了图像中每个点亮度梯度图以及亮度梯度的方向;
(4)某个像素的灰度值在其梯度方向上来比较梯度幅度,前后两个像素的灰度值之差不是最大时,就将这个像素值置为零,即不是边缘;较高的亮度梯度比较有可能是边缘;
(5)使用累计直方图计算两个滞后阈值。凡是大于高值阈值的一定是边缘;凡是小于低值阈值的一定非边缘。如果检测数据在两个阈值之间,则根据这个像素的周围邻接像素中是否有超过高阈值的边缘像素,如果存在,它就是边缘,否则不是。
5 实验仿真
将对以上常见算子进行图像实验仿真,对所采集的图像分别应用Sobel算子、Roberts算子、Log算子及Canny算子进行边缘检测,如图1所示。
由MATLAB工具处理结果可见,Sobel算子检测范围小,平滑噪声的作用一般,边缘粗而亮;对图像可抑制噪声,检测出的边缘较细,但边缘不够明显;Log的检测效果比Roberts算子好,边缘更清晰;Canny算子同样具有抑制噪声的能力,其检测出边缘较宽,信息丰富,边缘明显。通过比较可知,Canny算子的边缘检测最好。

图1 各种边缘算子比较
1.Rafael C Gonzalez,Richard E Woods.Digital Image Processing[M].Addison Wesley Publishing Company,2002
2.FreemanH,DavisLS.Acorne-finding algorithm for chain code curves[J].IEEE Transactions on Computers,1977,C-26(3):297-303
5.Rosenfeld A,Johnson E.Angle detection on digital curves[J].IEEE Transactions on Computers,1973,22(9):875-878
6.HarrisC G,StephensM J.A combined corner on edge detector.In 4th AlveyVision Conference[C]. Manchester 1988:147-151,189-192

