基于自适应变异粒子群算法的火力分配方法研究

欧 微,王克勤,朱 岑

(乌鲁木齐民族干部学院,新疆 乌鲁木齐 830002)

在信息化条件下,战场态势瞬息即变,基于智能算法的火力分配方法已经成为作战指挥中不可或缺的决策支持[1-3]。粒子群算法(Particle Swarm Optimization,PSO)是一种基于群体智能的进化算法,具有参数简单、收敛快速等优点,非常适合对复杂问题进行优化。但研究表明,基本粒子群算法(Basic PSO,BPSO)具有易陷入局部极值和早熟收敛等缺陷[4-6],因此许多学者或文献从不同方面对其进行了改进。如李凌等[7]在 Ratnaweera[8]的基础上,提出了一种惯性权重和加速因子自适应动态调整的改进策略,用于求解函数优化问题;文献[9]将模拟退火(SA)和禁忌搜索(TS)与 PSO 相结合,求解防空火力的目标分配问题;文献[10]通过对全部粒子重新初始化来保持种群的多样性,用于求解联合火力打击的目标分配问题。这些研究虽然有效地改进了BPSO算法的性能,但对于复杂的火力分配问题,其可行解空间是非常庞大的,一些近优解与最优解之间的编码可能存在巨大的差异,一旦陷入局部极值,则很难从中跳出。因此,需要在进化前期增强粒子的局部搜索能力,而在进化后期则需增强粒子群的多样性。因此,本文提出了一种 AMPSO,通过对惯性权重、认知因子和社会因子的动态调整,来保证算法在进化前期的局部搜索能力和进化后期的全局收敛性能,并通过设置变异池,控制部分粒子参与变异,保证在不破坏粒子群整体结构的基础上增强种群的多样性。

1 火力分配问题的数学模型

最优火力分配问题可描述为[10-12]:假定有M个火力单位处于战斗准备状态,对N个威胁目标进行打击,现需合理分配火力,使得敌威胁目标的整体毁伤价值最大。

令θj为第j个威胁目标的价值,Pij为第i火力单位对目标 j的摧毁概率,则火力优化问题的目标函数为

需满足的约束条件为

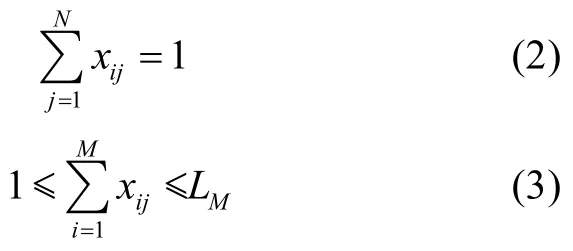
其中,i∈(1,2,…,M),j∈( 1,2,… ,N),LM表示最大集火规模;xij为0-1变量,若分配第i火力单位打击目标j则取 1,否则取 0;式(1)表明,要提高整体作战效能,应分配毁伤概率大的火力单位对目标进行打击,并应适度集中火力打击重点目标;式(2)表示任一火力单位在同一时刻只能打击一个目标;式(3)表示对任一目标,必须分配至少一个,最多LM个火力单位对其进行打击。

2 基本粒子群算法简介

BPSO算法是一种基于群集智能的优化算法。该算法模拟鸟群寻找栖息地的过程,将种群中的每个个体看作搜索空间中的一个没有体积和质量,以一定速度飞行的粒子,个体通过跟踪两个“极值”来更新自己,一是粒子本身找到的最优解,即局部极值rbest,另一个是整个种群目前找到的最优解,即全局极值gbest。第i个粒子在t时刻的速度和位置分别按式(4)和式(5)进行更新。

其中,Vi表示粒子i在t时刻的速度,Pi表示其在t时刻的位置,w为惯性权重,c1为认知因子,c2为社会因子,r1和r2为在区间[0,1]内均匀分布的随机数。

3 自适应粒子群算法的关键模块设计

BPSO算法具有参数设置少、收敛速度快等优点,但也存在一些局限性:1)将惯性权重、认知因子和社会因子设置为常数,难以同时保证算法的全局收敛效率和局部搜索性能。因此,应合理控制这三个关键参数的取值,以平衡算法的全局收敛效率和局部搜索能力;2)BPSO算法的全局收敛速度很快,容易导致种群多样性的快速丢失,当进化到一定阶段,所有个体将聚集到某个局部极值周围,出现早熟收敛的现象。因此在进化后期,需保持种群的多样性,以提高算法向全局极值搜索的能力。针对火力分配问题的特点和BPSO算法存在的局限性,本文采用十进制编码方法和基于实数运算的粒子更新方法,并对关键参数实施动态调整来平衡算法的全局收敛和局部搜索能力;针对种群早熟收敛的问题,设计了一种变异策略。

3.1 编码方法

目前,对于遗传算法、粒子群算法和混沌优化等智能搜索算法,主要存在两种编码方式:二进制编码和十进制编码。二进制编码虽然易于实现,但表现形式抽象,解码难度大,且编码较长,在运算时消耗的资源也较多;十进制编码方法则具有表现直观、易于理解和编码长度短等优点[6,13]。

本文采取十进制编码方法,将搜索空间中每一个可行解表示为一个长度为M的数组,数组中的每个元素均为介于[1,]N之间的正整数,元素的数值代表目标号,元素在数组中的排列号(元素在数组中的索引值加1)代表火力单位编号。在解码时,只需读取数组中各个元素的数值和排列号,即可获得相应的火力分配方案。如:Pi(t)=（2,1,3,2）,则表示第1、第 2、第3和第4个火力单位分别打击目标2、目标1、目标3和目标2。

可见,在编码中,所有元素的排列号是唯一的,从而能够满足一个火力单位在同一时刻只能打击一个目标的约束条件;同时只需检测编码中数值相等元素的个数,并进行简单修订,就能够按照战术要求合理控制集中火力的规模。因此,该编码方法能够实现可行火力分配方案到粒子搜索空间的有效映射,是一种求解火力分配优化的可行编码方法。

3.2 个体更新策略

考虑到粒子的飞行速度难以表达,大多数文献都采用遗传算法的交叉策略,即让当前个体与优秀个体交叉来更新粒子的位置信息。该方法虽然实现简单,但会破坏编码的整体结构,致使其违背约束条件。本文通过数值运算来更新粒子的速度和位置信息,粒子的速度为实数,位置为整数。在利用式(4)和式(5)更新粒子的速度和位置后,只需对位置向量中的各个元素向下取整,即可实现连续空间的离散化,获得更新后的位置信息。

比如,当搜索到第t+1代,假设由式(5)求得某个粒子的位置Pi(t+1)=( 2.6,1.3,1.8,3.4,4.2),分别对Pi(t+1)中各元素向下取整,即可得到更新后的位置信息Pi(t) = ( 2,1,1,3,4)。

3.3 关键参数调整策略

对于复杂的火力分配问题,其解空间维度较多,一些近优解与最优解的编码可能存在着较大的差异,若算法过早地收敛到某个近优解周围,则后期很难从中跳出。为了平衡算法的局部搜索能力和全局收敛效率之间的矛盾,本文采用惯性权重和社会因子随进化代数增加而递增,让认知因子随进化代数增加而递减的自适应调整策略,分别如式(7)、(8)和(9)所示。

其中,T为最大进化代数,t∈[1 ,2,…,T],表示当前进化代数,w( 0 )、c2(0)和c1( 0)分别为惯性权重、社会因子和认知因子的初始值,ξw、ξc2和ξc1为它们的控制参数。通过对这三个关键参数的动态调整,一方面能够提高算法在前期的局部搜索能力,使所有的粒子在其邻域内能充分进行搜索;另一方面可以逐渐增强算法的全局收敛性能,使种群能快速收敛到全局极值周围。

3.4 变异策略

对惯性权重等关键参数的调整,能较好地平衡算法局部搜索能力和全局收敛效率,但不能有效解决种群多样性快速丢失的问题。为此,本文设计了一种变异策略,针对参与变异的粒子,主要包含两种操作:1)在粒子中随机选择两个元素,交换其数值;2)重新初始化该粒子。

令Hs为种群规模,Rm为变异算子选择参数,t为当前进化代数,Tm为起始变异代数,tmΔ为变异周期,Hm为变异池规模,hm为当前变异池中粒子的个数。则变异策略的基本思想可描述为:

Step1 判断是否满足变异条件:若t＞=Tm且t%Δt==0,则转Step2,否则退出。

Step2 更新变异池:清空原变异池,并在种群中随机选择Hm个粒子,加入到池中。

Step3 变异操作:在区间[0,1]产生随机数Rand,若Rand＜=Rm,则对变异池中的粒子依次随机选择两个元素,将其数值对换;若Rand＞Rm,则对变异池中的粒子重新初始化。

Step4 更新种群:将变异池中的粒子替换原粒子,放入到种群中,之后退出变异操作。

可见,通过调整Rm和Hm的大小,可以有效地控制种群的整体结构和种群的多样性,进而提高算法在进化后期的搜索性能。

3.5 算法流程

综上所述,求解火力分配问题的AMPSO算法的基本流程如下:

Step1(初始化):设置初始参数,初始化种群。

Step2(适应度计算):计算种群中各粒子的适应度值。

Step3(极值更新):根据适应度值大小,更新种群的全局极值和各粒子的局部极值。

Step4(种群更新):根据式(7)、式(8)和式(9)更新关键参数信息;之后根据式(4)和式(5)更新种群中各粒子的状态。

Step5(变异操作):按照3.4节所述,对种群进行变异操作,生成新的种群。

Step6(终止准则):判断是否满足终止条件,若满足条件,退出;否则转Step2。

4 仿真实验及结果分析

假定我方共有10个火力单位对敌8个目标进行打击,现已对目标进行过价值评估,敌目标价值分别为:θj=( 0.4,0.95,0.35,0.9,0.5,0.95,0.7,0.6)各火力单位对目标的毁伤概率如表1所示。

表1 各火力单位对敌目标的毁伤概率

为验证算法的有效性,本文利用 C#编程语言,在Visual Studio 2010开发环境下,编写了仿真实验程序,分别利用BPSO和本文所提的AMPSO算法进行求解。其中,BPSO采用与AMPSO算法相同的编码和个体更新策略,选择火力优化的目标函数作为粒子群算法的适应度函数。

主要参数设置如下:种群规模Hs=3 0,循环代数T= 2 00,惯性权重、认知因子、社会因子的初始值分别为,其控制参数,起始变异代数Tms= 1 20,变异周期 Δtm= 5 ,变异池规模Hm= 6 ,变异算子选择参数Rm= 0 .4。

在其中的某次连续随机实验中两种算法的最优粒子适应度和种群平均适应度值收敛曲线分别如图1和图2所示。

由图 1可见,在进化前期,整个种群迅速向全局极值收敛,导致种群多样性的快速丢失;由于其局部搜索能力较弱,当进化到一定阶段(第 28代),其全局极值就已停止更新。可见,BPSO容易陷入局部极值,全局寻优能力不强。

图1 BPSO算法收敛曲线图

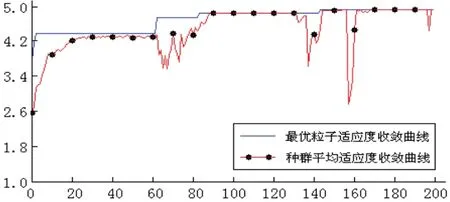
图2 AMPSO算法收敛曲线图

由图2可知,AMPSO算法在前期具有较强的局部搜索能力,所有粒子能够充分在其邻域周围进行搜索,算法表现出很强的跳出局部极值的能力;当进化到第90代,所有粒子收敛到当前极值周围,种群多样性消失;但在进化后期(120代以后),由于引入了变异操作,种群又呈现出一定的多样性,从而能跳出当前极值,进化到全局最优解。

分别利用BPSO和AMPSO算法随机进行20次实验,其统计结果如表2所示。

表2 BPSO与AMPSO试验结果统计

由表2可知,AMPSO在各次实验中最优解的平均适应度值为 4.8928,而 BPSO 仅为 4.5592,高出7.32%;AMPSO算法求得的最好解明显优于BPSO算法,且在实验结果中出现 4次,占到总数的 20%,表现出较高的寻优概率。

同时,AMPSO算法求得的最好解为4234178652,结合目标价值向量θj及表1可知:对于价值较高的目标2和目标4,分别分配了两个火力单位对其进行打击,符合“集中火力打击重点目标”的战术要求;对其它目标,均分别分配了毁伤概率最大的火力单位对其进行打击,符合“武器—目标匹配”战术原则。同样分析可知,对于 AMPSO算法出现的最差解4234278651,解码后生成的分配方案也同样具有较高的可行性。

上述分析表明,AMPSO算法具有比BPSO算法更好的搜索性能和寻优概率,由该算法求得的火力分配方案具有高度的可行性和全局最优性,能够有效发挥火力单位的整体作战效能。

5 结束语

如何实时、精确、最优地进行火力分配,是信息化条件下火力运用的关键问题。本文针对火力分配问题的基本特点,提出了一种求解该类问题的自适应变异粒子群算法。为验证算法的有效性,开发了仿真平台,并结合算例进行了大量的仿真实验。实验结果表明,所提算法具有较高的可行性,由该算法求得的火力分配方案可以作为指挥员指挥决策的科学依据。

[1]蔡怀平,陈英武.武器—目标分配(WTA)问题研究进展[J].火力与指挥控制,2006,31(12):985-989.

[2]董承博,谭守林,刘博.基于改进型多群体遗传算法的地地导弹火力分配[J].战术导弹技术,2010,33(5):36-39.

[3]王忠义,王钰.坦克分队火力运用与指挥[M].北京:海潮出版社,2004:113-120.

[4]Kennedy J,Eberhart R C.Particle Swarm Optimization [C].IEEE International Conference on Neural Networks,Perth,1995:1942-1948.

[5]Daniel Bratton,James Kennedy.Def i ning a Standard for Particle Swarm Optimization [C].Proceedings of the 2007 IEEE Swarm Intelligence Symposium,2007.

[6]欧微,邹逢兴,高政,等.基于多目标粒子群算法的混合流水车间调度问题研究[J].计算机工程与科学,2008,31(8):52-56.

[7]李凌,倪远平,孙婧雅.改进粒子群算法的研究与仿真[J].云南大学学报,2009,31(2):178-181.

[8]Ratnaweera A,Halgamuge S.Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients [J].Evolutionary Computation,2004,8(3):240-255.

[9]丁铸,马大为,汤铭端,张学锋.基于禁忌退火粒子群算法的火力分配[J].系统仿真学报,2006,18(9):2480-2483.

[10]张勇涛,余静,张松良.基于改进粒子群算法的联合火力打击目标分配研究[J].指挥控制与仿真,2010,32(1):41-44.

[11]张波,夏军,张福远.火力对抗条件下反坦克导弹目标分配优化[J].指挥控制与仿真,2009,31(6):56-58.

[12]陈华东,王树宗,王宇航.基于混合粒子群算法的多平台多武器火力分配研究[J].系统工程与电子技术,2008,30(5):880-883.

[13]刘志雄.求解调度问题的粒子群算法编码方法研究[J].武汉科技大学学报,2010,33(1):99-104.