基于模糊神经网络的坦克目标识别
郭 佳, 邓甲昊
(机电动态控制重点实验室,北京100081)
0 引言
目标识别技术是获取战场信息控制权的关键技术之一,指挥员只有在弄清楚目标的敌我属性、目标类型以及目标位置等参数后,才能下达攻击命令,武器系统也只有在得到各种目标参数后才能准确地击中目标。现代战场是陆、海、空、天和电子信息五维一体的作战空域,目标所处的自然环境和电磁环境以及目标的动态变化愈加复杂,指挥员决策更加困难。因此,传统的目标识别方法已不能满足现代战场需求,模糊神经网络由于结合了模糊逻辑功能与神经网络技术两种方法的优点,可以提高目标识别的准确性与识别率,本文着重研究基于模糊神经网络的目标识别技术。
1 目标识别方法与模糊神经网络的应用
1.1 目标识别方法简析
目前,针对不同的探测物理场环境,人们提出了多种目标识别方法,其中较为成熟的有:贝叶斯法、模板法、表决法,还有随后发展起来的登普斯特-谢弗法、神经网络法、专家系统法等[1]。
通常战场铁磁目标的磁场信号复杂,并且由于自然或人为因素的存在,常表现出模糊性、不确定性、甚至是欺骗性等特征,所以运用传统的统计分类或物理建模的方法已不再适应战场要求,基于此种背景,需对智能识别算法加以研究。模糊神经网络是将处理不确定信息能力的模糊逻辑功能与具备知识存储能力的神经网络技术结合起来,因此将其应用于战场铁磁目标的识别,可以提高识别率。
1.2 模糊神经网络及应用
模 糊 神 经 网 络(Fuzzy Neural Network,FNN)将模糊系统与神经网络相结合,充分考虑了二者的互补性,集逻辑推理、语言计算、非线性动力学于一体,具有学习、联想、识别、自适应和模糊信息处理等功能[2]。
在模糊神经网络中,神经网络的输入、输出节点用来表示模糊系统的输入、输出信号,神经网络的隐含节点用来表示隶属函数和模糊规则,利用神经网络的并行处理能力可使得模糊系统的推理能力大大提高。
自适应模糊神经推理系统,也称为基于神经网络的自适应模糊推理系统(Adaptive Neural-Fuzzy Inference System,ANFIS),融合了神经网络的学习机制和模糊系统的语言推理能力等优点,弥补了各自的不足。同其他模糊神经系统相比,ANFIS 具有便捷高效的特点,已被收入MATLAB的模糊逻辑工具箱,并在多个领域得到了成功应用。
1.3 ANFIS的模型初始化及genfis1函数
ANFIS模型初始化任务主要是初步确认隶属度函数类型及其参数。在MATLAB模糊工具箱中,参数fismat用于指定初始ANFIS 模型的专用矩阵,可使用函数genfis1由训练数据直接生成,genfis1采用网格分割的方法根据给定数据集生成一个模糊推理系统。该系统的输入和输出隶属度函数曲线既能覆盖整个输入输出空间,又能对其进行均匀分割。genfis1 的主要作用是确定一个合适的初始模糊系统的结构(隶属度函数个数,模糊规则数目),anfis训练不会改变genfis1已经给定的初始模糊推理系统的结构,只是对相应的结构参数进行调整和优化,该函数生成的系统总规则数等于所有输入变量的隶属度函数个数的乘积。
2 坦克目标磁场模型建立
用模型化方法研究战场铁磁目标,可以充分利用其磁信号的时频特性、磁场矢量的空间分布特性以及目标的运动特性,是磁场的准全息技术[3,4]。若能可靠地建立起铁磁目标的磁场模型,利用最能体现描述目标磁场本质特征的几个主要模型参数,作为目标识别的特征量,结合新型非晶丝磁探测器,有望在保证较高正确识别率的情况下,显著提高对目标的探测距离。
坦克受地磁场的作用而磁化,产生坦克磁场,可将其分为固定磁性磁场和感应磁性磁场两部分。固定磁场主要是坦克长期停留在某一方向上经受地磁的磁化而形成的磁场,其性质属于剩磁,远小于坦克的感应磁性磁场。因此,本文坦克磁场的建模主要围绕坦克感应磁场进行。
用一个稳定的磁场数理模型可以较精确地推算出实际磁场信号的空间分布特征和时频特性,从而有效提高目标识别的准确率。陆地战场上的铁磁目标以坦克、装甲车、军用卡车等最为典型,均为一定几何形状的磁性体。以坦克为例,采用单一旋转椭球体对坦克磁场进行模拟[5,6],虽然坦克近场精度差,但随距离增大,拟合精度越来越高,而且模型参数较为稳定,故可作为弹目距离较远时坦克目标识别的特征量,图1为单一旋转椭球体模型示意图。
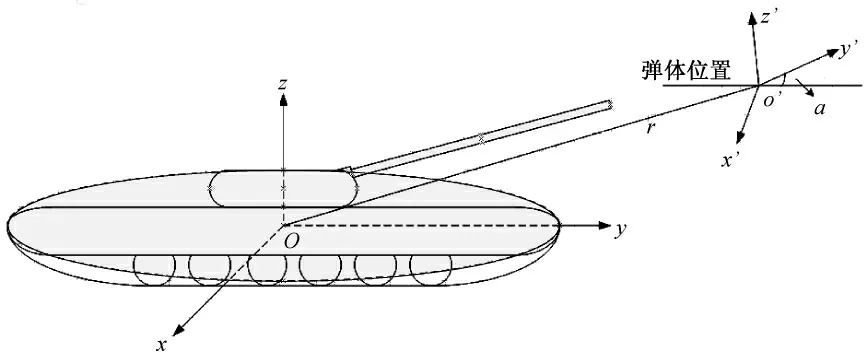
图1 坦克磁场模型示意图
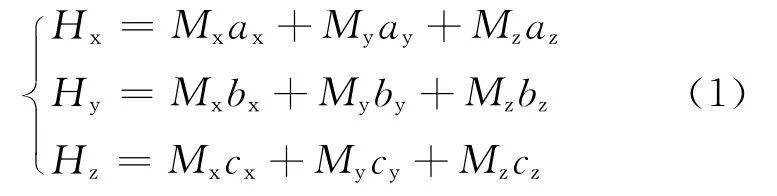
式中:[Mx,My,Mz]为椭球体模型的磁矩,系数矩阵[ax,ay,az]T,[bx,by,bz]T,[cx,cy,cz]T分 别定义如下[7]:
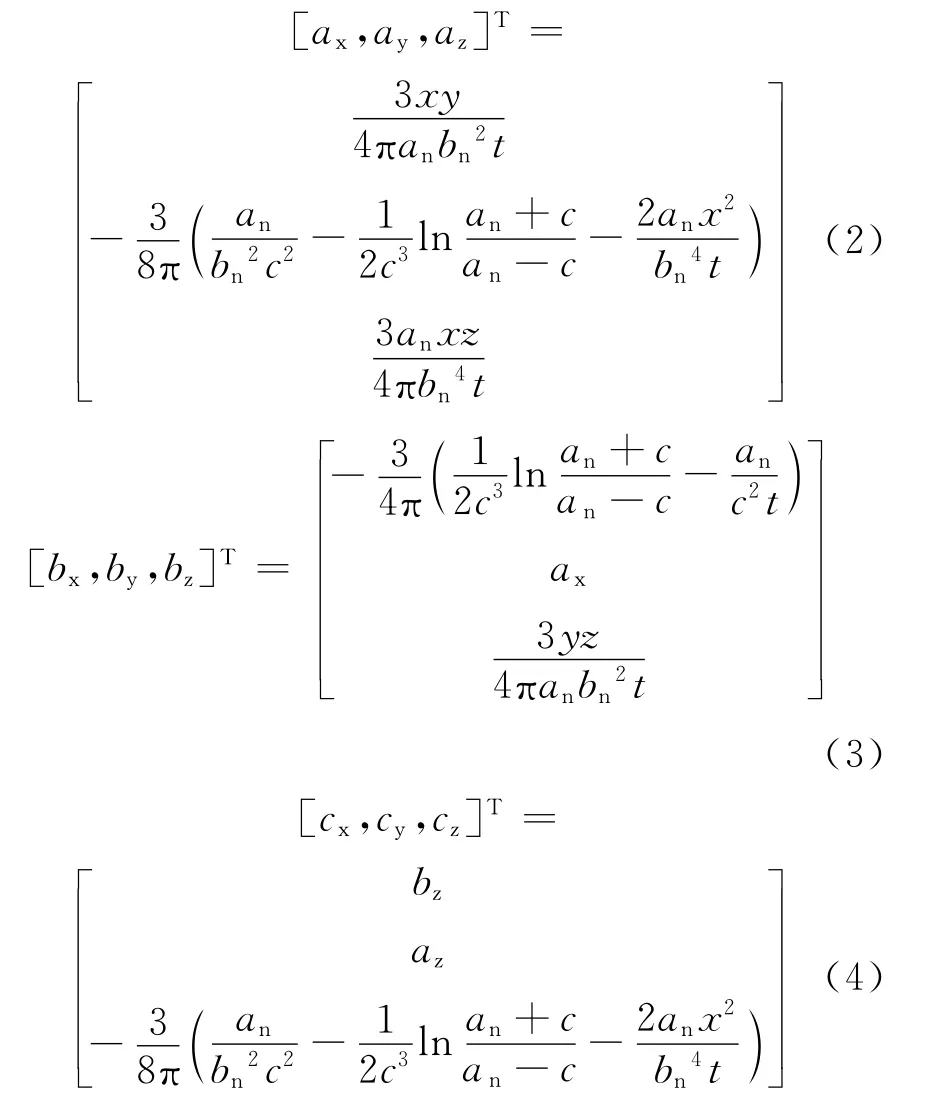
式(2)~(4)中t,an,bn定义如下:
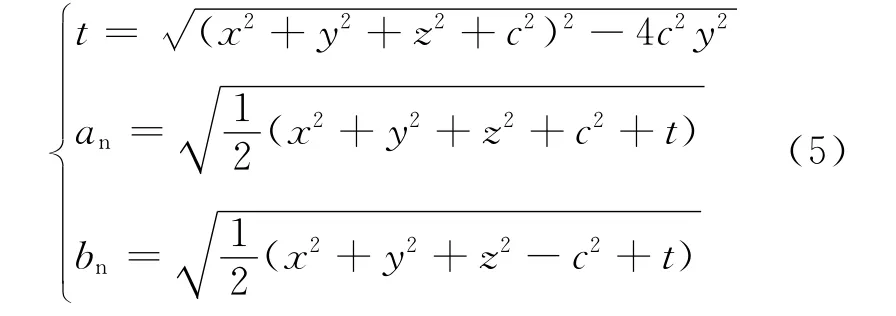
根据式(1)三个磁场分量模型,可以计算出坦克不同区域的磁场分布。
3 模糊神经网络识别系统设计
自适应模糊神经网络是基于数据建模的方法,其模糊隶属度函数及模糊规则是经过大量已知数据的学习而得到的,可以说自适应模糊神经网络是基于数据规则的识别,因此要进行模糊神经网络识别首先要建立模糊规则库。
3.1 模糊规则库的建立
由前文可知,期望的输入-输出数据偶:Mx,My,Mz,c→y 其中Mx,My,Mz,c 为根据旋转椭球体建模的磁性目标模型参数,y 为识别结果。在模糊系统中,将输入空间和输出空间划分为模糊空间,每个区间有相应的模糊隶属函数。根据不同区间 上 已 知 数 据Mx,My,Mz,c 和y 相 应 的隶属度,将输入、输出参量定位于最大隶属度对应的区间上,从每一条满意的输入-输出数据对产生一条规则。
3.2 设计实现过程
对于陆地战场,磁探测系统接收的磁信号主要来自坦克、普通军用卡车、自然干扰信号(磁暴、地磁脉动等)、工业干扰及电路噪声等。对于后两类干扰信号,虽然频率范围较宽,可以完全覆盖目标磁场信号的频率范围,但是因其不能用一个均匀磁化的旋转椭球体来拟合,通常难以通过模型检验;而军用卡车和坦克在几何形状、材料构成以及重量等方面具有很大的相似性,是磁探测系统需要重点区分的内容。所以本文定义一个三位二进制数组T(T1,T2,T3)作为模糊神经网络的输出值。它存在八种可能的输出,分别对应坦克和卡车的各个行驶方向,具体含义如表1所示。
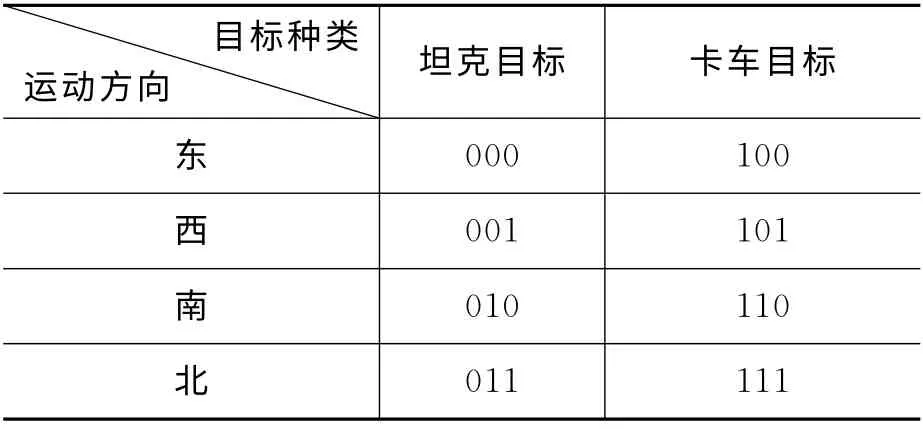
表1 网络输出值含义
为提高系统目标识别的可靠性,对我国某主战坦克以及解放型卡车进行了实测,并对用非晶丝磁探测器获得的数据进行了预处理,求出目标运动方向为东、西、南、北四个方向时,旋转椭球体的模型参量Mx,My,Mz,c,并进行了归一化处理,作为模糊神经网络的输入。表2为部分输入输出样本。
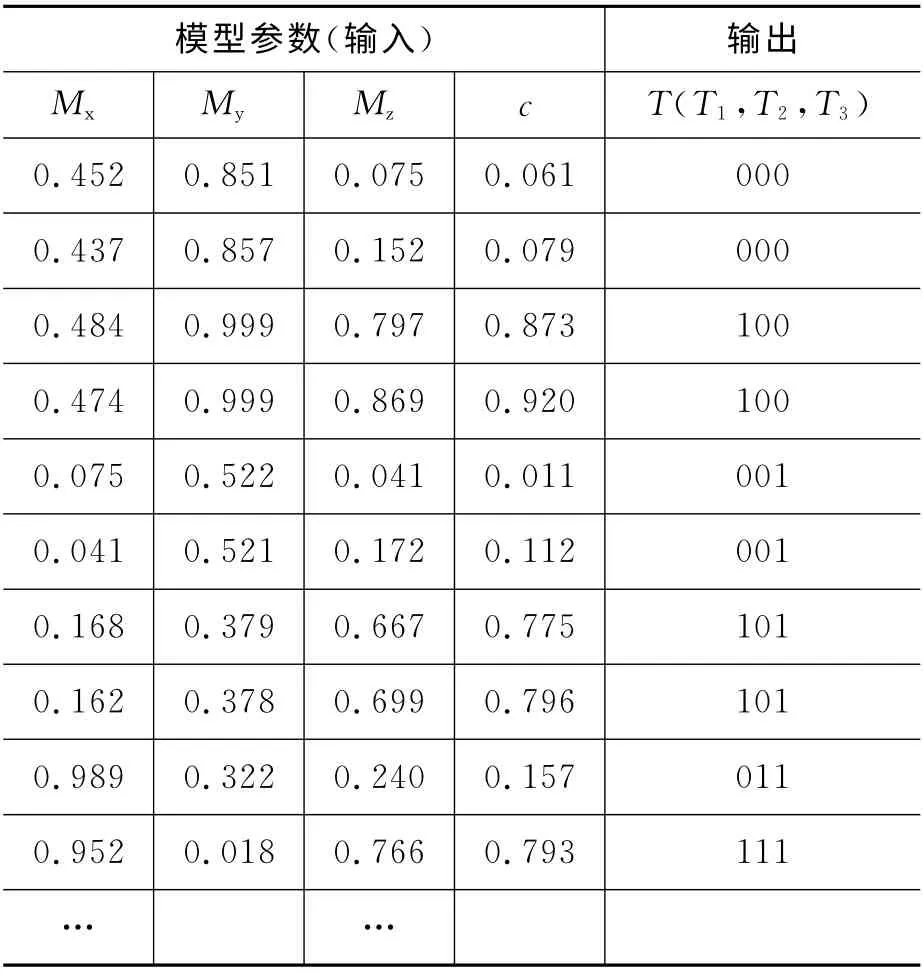
表2 输入输出样本
按表2数据建立自适应模糊神经网络系统,利用MATLAB模糊逻辑工具箱,打开ANFIS编辑器,编辑ANFIS属性,定义输入输出变量隶属函数,设置模糊规则库。
图2显示了genfis1根据训练数据生成的模糊推理系统初始隶属度函数曲线,可以看出,函数genfis1按照均匀覆盖输入空间的原则构造了初始隶属度函数。
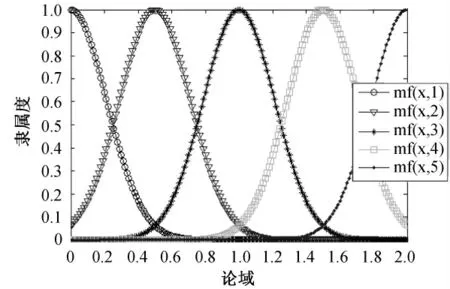
图2 初始隶属度函数曲线
图3为最终模型的隶属度函数曲线,可以看出,经过学习后的模糊推理系统提取了训练数据的局部特征,与图2比较知,最终隶属度函数不再均匀覆盖输入空间,其变化反映了输入输出数据对的变化特征。
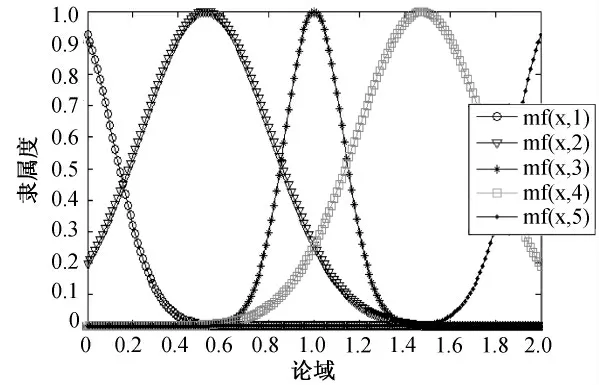
图3 训练后模糊推理系统的隶属度函数
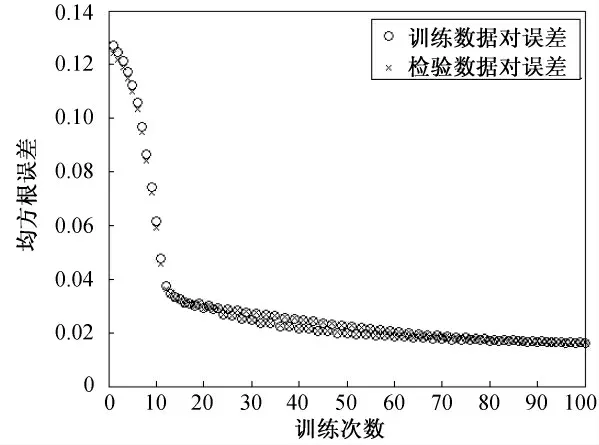
图4 训练过程中均方根误差变化曲线
图4为训练过程中均方根误差的变化曲线。由图4可以看出经过100次的函数训练,训练误差和检验误差均在0.02以下,很好地拟合了系统的实际状况。
4 结束语
由理论分析及仿真实验结果可知,运用模糊神经网络对坦克目标进行识别是可行的。模糊神经网络在目标识别和处理不确定性数据上有其独特的能力,它将比传统的目标识别方法更有效、准确。
[1] 帅艳民,李孝词,刘峰.基于模糊神经网络的舰船目 标识别的方法研究[J].镇江高专学报,2001,14(3):39-42.
[2] 李国勇.神经模糊控制理论及应用[M].北京:电子工业出版社,2009.
[3] 林春生,向前,龚沈光.水中磁性运动目标信号的模型化检测[J].兵工学报,2005,26(2):192-195.
[4] 王海云,董大群.舰船磁场模型参数在目标识别中的应用[J].船舶工程,1999,(3):46-49.
[5] 陈正宏,费保俊,等.坦克外部磁场的有限元分析[J].装甲兵工程学院学报,2005,(1):90-92.
[6] 孙骥,邓甲昊,高珍,等.一类新型非晶丝微磁探测器在坦克静态磁场分析中的应用[J].北京理工大学学报,2009,29(2):95-99.
[7] 叶平贤,龚沈光.舰船物理场[M].北京:兵器工业出版社,1992.

