基于同质多物品拍卖的股权定价研究

郑君君 张 平

基于同质多物品拍卖的股权定价研究

郑君君 张 平

IPO市场中存在着信息不对称的问题，风险投资家往往不知道外部投资者的真实估价，导致最终无法实现资源的最优配置。引导外部投资者采取“说真话”策略的关键在于制定一套有效的激励约束机制。拍卖是一种可以满足激励相容和个人理性的有效市场机制，基于同质多物品拍卖理论来进行机制设计，激励外部投资者揭露真实信息，最终实现资源的最优配置。

同质多物品拍卖；信息不对称；激励相容；个人理性

当风险项目成熟时，风险投资家会将手中持有的股权出售，从而实现风险投资的退出，IPO（Initial Public Offering）是最理想的风险投资退出方式之一，风险投资家可以通过IPO市场实现高额的投资回报。然而，在股权拍卖时外部投资者往往“说假话”，风险投资家无法知晓其真实估价，最终可能导致资源配置不合理和帕累托法则无效的分配结果。

拍卖作为一种有效的资源配置方式和价格发现机制，正是可以满足激励相容和个人理性的市场机制，所以，通过合理的拍卖机制设计可以克服信息不对称造成的经济损失。J.J.Laffont（1980）认为，机制设计理论需要解决的根本问题是不对称信息条件下的激励问题，因此需要实现激励相容和个人理性这两个基本的约束条件①J.J.Laffont，E.Maskin.“A Differential Approach to Dominant Strategy Mechanisms.”Econometrica，1980，48（6），pp.1507～1520.。本文将IPO市场中的股权视为同质多物品，通过激励外部投资者揭示自身的真实信息来实现风险投资家拍卖收益最大化，为IPO市场中风险投资家和外部投资者的委托—代理提供参考。

一、机制设计

最优拍卖机制包含在满足激励相容条件的直接显示机制之中，在这些机制下，竞买人如实报告私人估价是一个弱占优的策略。用函数（p，c）表示直接拍卖机制，p（v）和c（v）定义在所有竞买人的估价支撑的乘积空间V上，分别代表着拍卖中的配置和支付。N＝｛1，2，…，n｝为竞买人的集合，vi∈［ai，bi］是竞买人i的真实估价，ri为报出的价格，可得V＝［a1，b1］×…×［an，bn］，pi（v）∈［0，1］表示竞买人i获胜的概率。

当其他人都真实报价，外部投资者i报价为ri时，其期望剩余为真实估值和实际支付之间的差额：其中，分别表示除外部投资者i外其他外部投资者均报告真实估价的估价向量和概率分布。

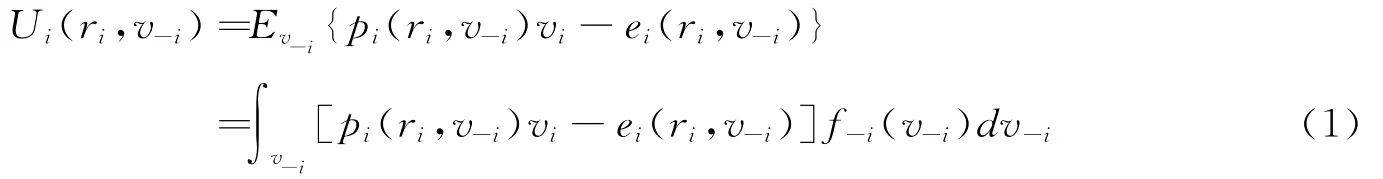
个人理性约束指竞买人参与拍卖所获得的期望效用不能小于其保留效用，假设期望剩余为a时，∀vi∈［ai，bi］均有Ui（vi，vi）≥a。激励相容约束指卖方要提供足够大的激励促使买方揭露自己的真实信息，报告真实的估价，这就要求竞买人报告真实估价时所得到的效用不小于报告其他的估价所得到的效用，即要求∀vi，ri∈［ai，bi］，Ui（vi，v－i）≥Ui（ri，v－i），还可以表达为

风险投资家在IPO市场中出售持有的股权来实现投资回收，故在本文所设计的拍卖机制中，拍卖的标的为风险投资家欲减持的风险企业股权。假设在IPO过程中，总共有m份相同且不可再分的股权，风险投资家即为机制设计者，其目的是通过激励外部投资者揭示真实估价以实现拍卖收益的最大化。

假设1：采取同质多物品拍卖的方式，将要出售的股权分成完全相同且不可再分的m份。

假设2：买方和卖方均为风险中性，即当拍卖参与者i的收益为πi时，其效用为U（πi）＝πi。

假设3：外部投资者拥有股权的私人信息，表示为Ti，仅凭私有信息就能对物品进行估价。风险投资家不能观察到Ti的值，认为Ti服从概率分布FTi（·），取自和Tj（i≠j）相互独立。

私有信号向量T＝（T1，…，Tn）分布在向量支撑集M＝M1×…×Mn上；T－i＝（T1，…，Ti－1，Ti＋1，…Tn）为除i外其他外部投资者的私有信号向量，分布在M－i＝M1×…×Mi－1×Mi＋1×…×Mn上。

假设4：各个外部投资者之间是非合作博弈关系，不存在共谋现象。

假设6：对附加单位物品的期望估价是非增的，即对所有的t，均有：

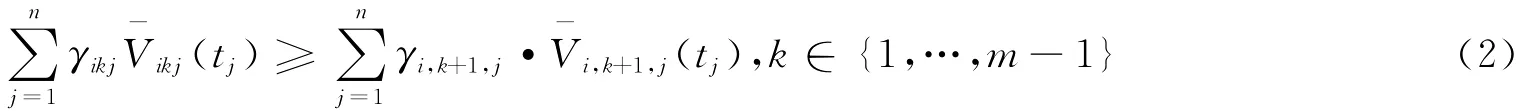
假设7：期望估价满足如下正则条件，对任意ti和都有：

假设6和假设7体现了边际效用递减原则，表明买方赢得第k＋1个物品所获得的收益不大于赢得第k个物品的收益。

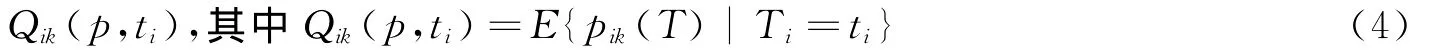
为了便于刻画，将外部投资者i至少赢得k个物品的概率记做基于以上假设条件，风险投资家可以设计如下满足激励相容和个人理性的拍卖机制：

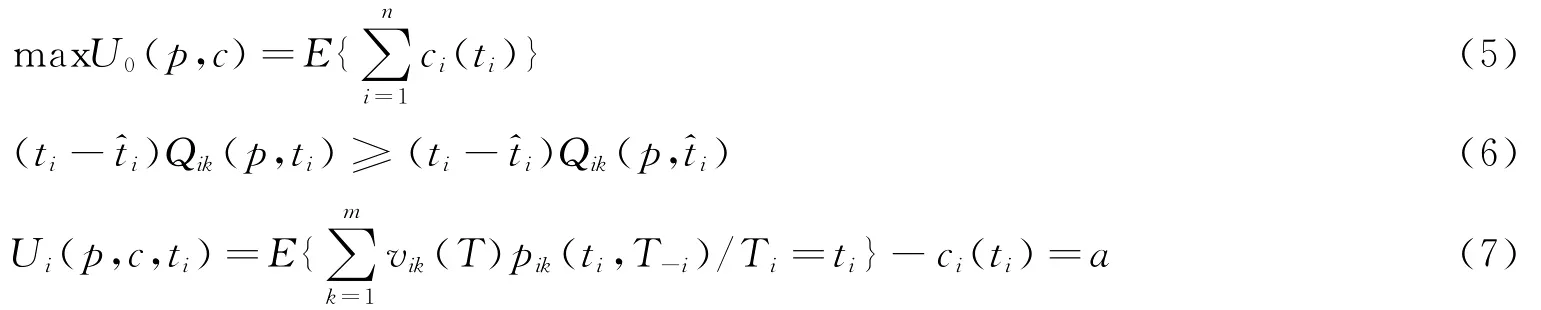
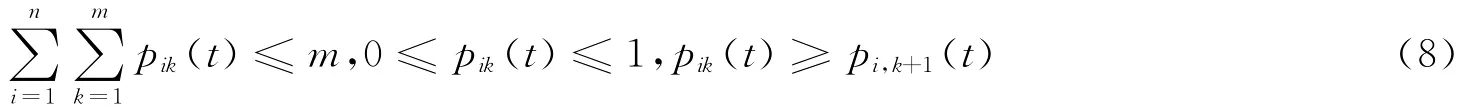
其中：

（1）vik（T）和pik（T）分别表示外部投资者i从风险投资家手中购得k份股权的真实价值和概率，ci（T）为赢得股权所付出的成本。

（2）式（5）要求风险投资家的利益最大化，效用是外部投资者的支付之和.式（6）表明（p，c）是激励相容的，外部投资者诚实的报告私有信息是一个弱占优的决策；式（7）表示外部投资者获得的预期收益为a，包含了通过“说假话”降低最终支付而获得的额外收益；式（8）是数量约束条件，拍卖的股权不超过m份，外部投资者从风险投资家手中购得至少k份股权的概率介于0和1之间，符合实际条件。

考虑到假设条件5，式（2）中的激励相容约束条件可以用如下的方式表达：表示在预计其他外部投资者估价

的影响时，外部投资者i如实报告真实信息仍然是弱占优的决策。

当风险投资家的剩余期望效益为零时上述拍卖机制为最优拍卖，模型如下：

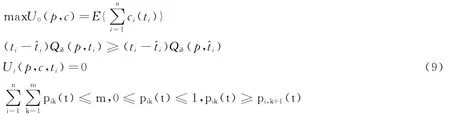
式（9）说明外部投资者不能通过说假话获得额外的收益，风险投资家有效地揭示了其私有信息。

假设2中π为收益，外部投资者i购买第k份股权支付πik（·），风险投资家获得πik（·）的收益。最优拍卖机制要求出售的股权对于外部投资者的效益最大，所以，对πik的排序非常关键。其中：πik（t）并且风险投资家收到外部投资者的私有信号的报告并计算出πik（t），将会从最大的π中选择股权的配置。

（1）分配规则：风险投资家根据每个外部投资者的私人信号报告计算出对应的收益，将会把股权出售给收益最高的外部投资者，则有：

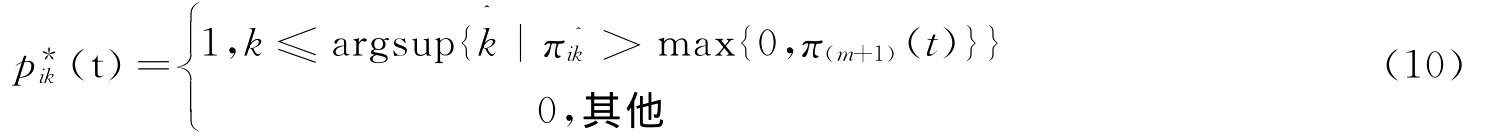
（2）支付规则：风险投资家收到的私有信号等于外部投资者的最大赢得信号，则其期望支付一定为几个物品期望价值之和，即：

一套最优拍卖机制应该保证对拍卖物品估值最高的投标人赢得拍卖物品，同时拍卖者获得最大的期望收益。在本文的拍卖条件下，最优拍卖机制应该使得风险投资家的效益最大化，同时将股权分配给真实估值最大的外部投资者。研究本文的同质多物品拍卖机制可以得出如下结论：

（1）买进第k份股权的外部投资者是最有效的买方，亦即效用最大的买方。通过激励相容条件获得外部投资者的真实报告，从而对每个外部投资者的效益排序，最终选择最大的效益进行股权配置。

（2）风险投资家的期望效益和在最优拍卖机制中的期望效益是相等的。已经知道买进第k份股权的外部投资者是最有效的买方，并且对于本文中的确定性拍卖，拥有最高可行估价信号的外部投资者的期望剩余为零，在满足外部投资者的私人估价相互独立并且严格递增的假设条件下，由收入等价原理可知，本文所设计的多物品拍卖机制带给风险投资家的收益和最优拍卖机制中的收益相等。

二、算 例

某高新技术项目成熟时，风险投资家S欲出售2份相同的股权，现存在潜在的投标者B1和B2，并且需求的股份份额均为2份，投标者B1的真实估价为28万元、27万元，报价为26万元、25万元；投标者B2的真实估价为30万元，29万元，报价为27万元，24万元。风险投资家考虑到投标者有“说真话”和“说假话”两种情况，设计了有激励和无激励两种机制，在有激励条件时，竞标者赢得每份拍卖品将获得拍卖出清价格（未赢得拍卖品的竞价者中的最高竞价）的r的返现（r＝0表示无激励）。

表1 投标者的报价及分配、支付示意

由表1可知，B1和B2说真话时分配结果更优，两份股权均分配给具有更大效用的B2。

鼓励竞买人B1和B2诚实地报告私人估价之后，第二份股权分配在B1和B2之间发生了转移，为了实现这一转移，风险投资家将补偿B1c1万元，从B2抽取c2万元的佣金，并且对每份股权给予市场出清价格的r倍的激励，所以，出现了两类激励：转移激励和售后激励，那么激励约束表示为：

对B1：c1≥28－27

对B2：28r≥c2＋（30－27）

此时风险投资家获得的收益增长为：（30＋29）－（27＋26）＋c2－28r×2－c1＝2×（3－28r）＋c1＋c2

可以得出以下结论：对于B1的补偿c1必须大于说假话的期望剩余，对于B2来说抽取的佣金c2和r之间为线性关系，呈反比例，最终风险投资家收益的期望增长不大于（c1－c2），但最终实现了资源的最优配置同时发现了股权的真实价值。

结 论

IPO市场中外部投资者和风险投资家之间存在着信息不对称，导致资源配置无效、股权真实价值无法揭示，风险投资家需要设计合理的机制，激励外部投资者揭露自己的真实信息，以求尽量减少上市过程中的损失。对此问题，本文尝试运用拍卖机制设计的方式求解，由于股权是一种典型的可分割多物品，本文设计了有效的同质多物品拍卖模型，通过激励相容条件使得外部投资者揭露真实信息，最终实现资源的最优配置、发现了股权的真实价格，从理论上也证明了这个拍卖机制是最优拍卖机制。

郑君君，武汉大学经济与管理学院教授，博士生导师，博士；湖北 武汉430072。张 平，武汉大学经济与管理学院硕士生。

国家自然科学基金项目 （71071120）

于华东