T型半导体量子线的动态屏蔽效应

刘 月 王廷栋 白凌志 程 诚 张 伟 怀 平

(中国科学院上海应用物理研究所 上海 201800)

半导体量子线系新型半导体纳米材料，是基于两个半导体量子阱界面处的量子限域效应而形成的准一维系统[1]，可望应用于发光器件等领域。近年来制备出矩形、T型、V型截面的量子线，并开展了大量的光谱学研究[2–14]。实验结果表明，半导体量子线激光器相对半导体量子阱激光器具有低阈值、高增益等特性[15,16]。

由于半导体量子线载流子处于受限环境，其受光激发特性有待进一步研究。例如，在一维半导体系统中，由于库仑相互作用使电子与空穴形成复杂状态(有激子、双激子、激子气体、激子液滴及电子-空穴等离子体)，其吸收谱具有复杂结构。研究表明，掺杂的半导体量子线存在费米面吸收等特性[17,18]。半导体量子线是探索一维电子-空穴体系物理的合适体系，也因其潜在应用而广受关注。

本文研究光激发的一维半导体量子线的量子限域效应及多体效应对其光学性质的影响。相比二维结构的半导体量子阱，准一维系统半导体量子线中载流子间的相互作用因很强的量子限域效应而加强[19]。在半导体研究中，载流子间的库仑相互作用带来了复杂的多体效应，如能带重整化、光吸收增强等效应[17,20]。当受激产生的电子-空穴气体浓度较低时，电子-空穴间的库仑作用较强，二者结合形成激子-中性的准粒子；当受激产生的电子-空穴气体浓度较高时，库仑作用被带电载流子自身所屏蔽，强度大为减弱而无法束缚电子-空穴，形成电子-空穴等离子体[1]。从低浓度的激子气体到高浓度的电子-空穴等离子体的转变过程称为 Mott相变[2]。文献[2,4,11]发现 Mott相变过程中激子、双激子和等离子体的光谱学特性。由于高浓度电子-空穴体系中存在很强的库仑屏蔽效应，导致半导体的光学吸收谱和光致发光谱的峰位置发生红移和谱学展宽。这些现象对应于激子束缚能、带隙及载流子散射强度伴随电子-空穴密度增加而增强的效应。

1 理论模型

以 GW近似为基础，分别采用动态PPA (Plasmon-Pole Approximation)和准静态PPA计算了不同截面尺度的T型半导体量子线的能带重整化和载流子自能，并对其结果进行比较。我们考虑理想的二能带模型，无相互作用的电子和空穴的能量分别为：εe,k=(ħk)2/(2me), εh,k=(ħk)2/(2mh)+ Eg0，其中，me和mh分别为电子和空穴的有效质量，Eg0为不含能带重整化时的带隙。

1.1 PPA理论和GW近似

在PPA理论中，准一维体系的介电函数如下表示为[1,21–23]：

式中，k为动量，ωpl(k)为一维等离子频率，ωk为有效等离激元频率，δ为描述载流子寿命相关的衰减常数[1,21–23]。

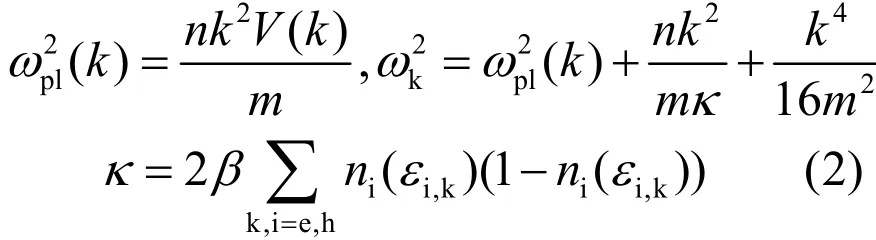
其中，V(k)为无屏蔽的有效库仑势；m为电子与空穴的折合质量，1/m=1/me+1/mh；κ为屏蔽常数；β=1/(kBT)；ni(ε) =1/(eβ(ε–μi)+1),为费米分布函数, μi为粒子的化学势，且在温度和粒子浓度确定时可通过∫dk/(2π) ni(ei,k)= n求解，ei,k=εi,k+Δi(k)，Δi(k)为能带重整化能量。

基于GW近似的单粒子自能为[22,23]：

其中，Gi(k,z)=1/(z–ei,k+μi)为松原格林函数(Matsubara Green Function)，Vs(k,z)=V(k)/ε(k,z)为动态屏蔽库仑势。

1.2 动态PPA下的单粒子自能

式(3)中的动态屏蔽库仑势 Vs(k–k',z–z')可通过PPA理论得到，将松原格林函数和动态屏蔽库仑势代入式(3)，并对z'求和得到动态PPA理论计算的单粒子自能为[18,22,23]：

其中，nB(ε)=1/(eβε–1)为玻色爱因斯坦分布函数。我们称式(4)右边第一项为关联自能，第二项为屏蔽交换自能[1,22,23]。由于存在虚数iδ，动态PPA理论计算的单粒子自能包含实部和虚部两部分:

1.3 准静态PPA下的单粒子自能

将式(3)中的Vs(k–k', z–z')替换成Vs(k-k',0)称为静态近似，这样仅得到屏蔽交换自能，致使这种方法不能给出精确结果。比静态近似精确的是准静态近似，即忽略散射中的反冲能量 ei,k–ei,k'。因此，准静态近似下能带重整化表示为[22]：

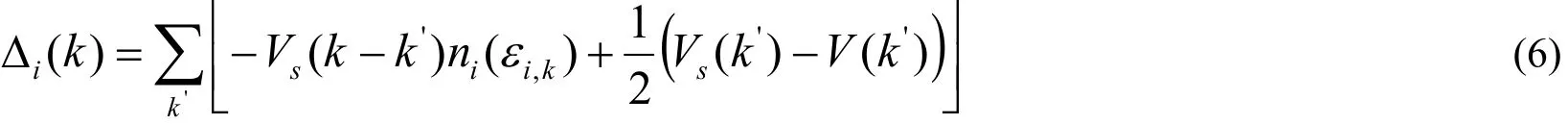
其中，Vs(k)=Vs(k,0)=V (k)/ε(k,0)是静态屏蔽库仑势，可通过PPA理论求得，我们称此方法为准静态PPA。

1.4 有效库仑势

在准一维量子线体系中，若不考虑屏蔽效应，载流子间的有效库仑相互作用可采用包络近似计算[15,22]：

其中，i和j是能带，k是动量，κ0为第二类修正Bessel函数。本文me=0.0665m0, mh=0.457m0，砷化镓体材料的激子玻尔半径a0=12.5 nm和激子束缚能E0=4.2 meV，φ(x,y)为载流子在量子线截面处的包络函数。

考虑到多体效应的影响，为简化计算，采用无限高势垒近似，即载流子完全束缚在量子线中。在无限高势垒近似下，电子-电子、电子-空穴、空穴-空穴间的有效库仑势相同[15,22]，记为V(k)。图(1)为由式(7)算得的不同截面尺度 T型量子线的有效库仑势，内嵌框图为T型量子线的横截面示意图。Lx、Ly为横向和纵向的阱宽，计算中使用的包络函数为：

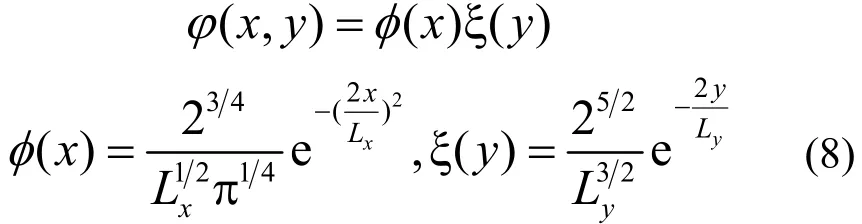
式中，φ(x)和ξ (y)分别为x和y方向的基态波函数。由图1，量子线的有效库仑作用在k→0处发散，逼近于‒lnk；当k→∞时，有效库仑势趋于0。具有一定截面结构的电荷分布在无穷远处，可视为作点电荷，即此结果逼近点电荷的库仑势。上述三种截面尺寸半导体量子线的有效库仑势随截面尺度减小而明显增强。表明一维体系对载流子的束缚随截面尺度的减小而增强，库仑作用在受限体系中显著增强是低维系统的共同特征。理论表明，当截面尺度趋于无限小时，有效库仑势趋于无限大。但实际半导体系统中由于有限势垒的约束，载流子易从量子线中泄漏，故不能实现很强的量子限域效应。

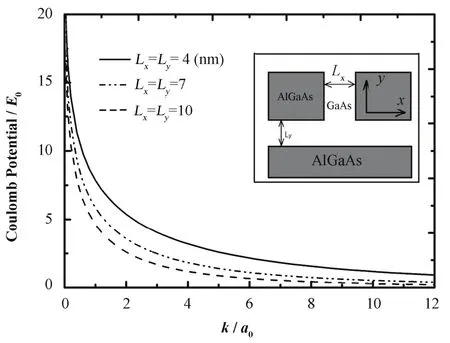
图1 不同截面尺度的T型量子线中的有效库仑相互作用Fig.1 Effective Coulomb potentials of T-shaped semiconductor quantum wire Vs. cross-section size.

2 计算结果与讨论

准静态PPA下电子能量ee,k–Eg0=εe,k+Δe(k)–Eg0和空穴能量eh,k=εh,k+ Δh(k)随动量的变化见图2，计算所用粒子浓度为ne=nh=106cm–1，温度为100 K。准静态PPA下的电子能量和空穴能量随量子线截面尺度的减小而发生较大移动。当载流子受到的约束增大时，它们间的有效库仑作用变强，多体作用带来的能带重整化效应也增强，带隙变小。

图3为动态 PPA下电子能量的实部 Re[∑e(k, ee,k–μe)]+εe,k–Eg0和空穴能量的实部 Re[∑h(k, eh,k–μh) ]+ εh,k。计算中δ=0.5 meV，粒子浓度为ne= nh=106cm–1，温度为100 K。由图3 (a)，若不考虑库仑作用，采用有效质量近似的半导体量子线的电子动能呈抛物线形状[1]。具有动态屏蔽的库仑作用明显改变了电子能带的形状，当电子能量与等离子体的共振频率接近时，由于强烈的散射效应，电子能量显著减小，电子能带出现极小值。当有效库仑作用随量子线尺度减小时，散射效应增强，从而形成更大的能带重整化效应。

从图3 (b)和图2(b)可见，同一截面尺度下采用准静态PPA和动态PPA计算所得空穴能量实部接近，这是由于空穴的有效质量大于电子，具有较大动能，因此不易发生类似电子的强烈散射效应。

图2 准静态PPA下T形量子线的电子(a)与空穴(b)的能带Fig.2 Energy bands of electron(a) and hole(b) of T-shaped quantum wire in static PPA.—— Lx = Ly = 4(nm), - - - Lx = Ly = 7, −·−· Lx = Ly = 10

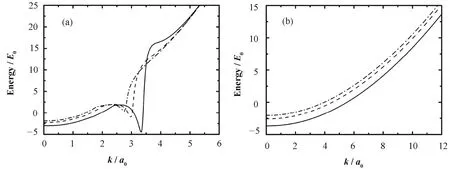
图3 动态PPA近似下T型量子线的电子(a)与空穴(b)的能带实部Fig.3 The real part of energy bands of electron (a) and hole (b) of T-shaped quantum wire in dynamic PPA.—— Lx = Ly = 4(nm), - - - Lx = Ly = 7, −·−· Lx = Ly = 10

图 4为动态 PPA下电子能量的虚部 Im[∑e(k, ee,k–μe)]和空穴能量的虚部 Im[∑h(k, eh,k–μh)]。自能的虚部对应于准粒子的寿命，自能虚部中的极值与此处的强烈散射有关。由图4可见，电子能量的虚部极值位置随截面尺度的减小向 k变大的方向移动，与图3(a)所示的能量突变位置相同，进一步表明有效库仑作用带来的散射效应随量子线截面尺度减小而增强。而图4(b)的空穴自能虚部与电子相比很小，来源于较大的有效质量。

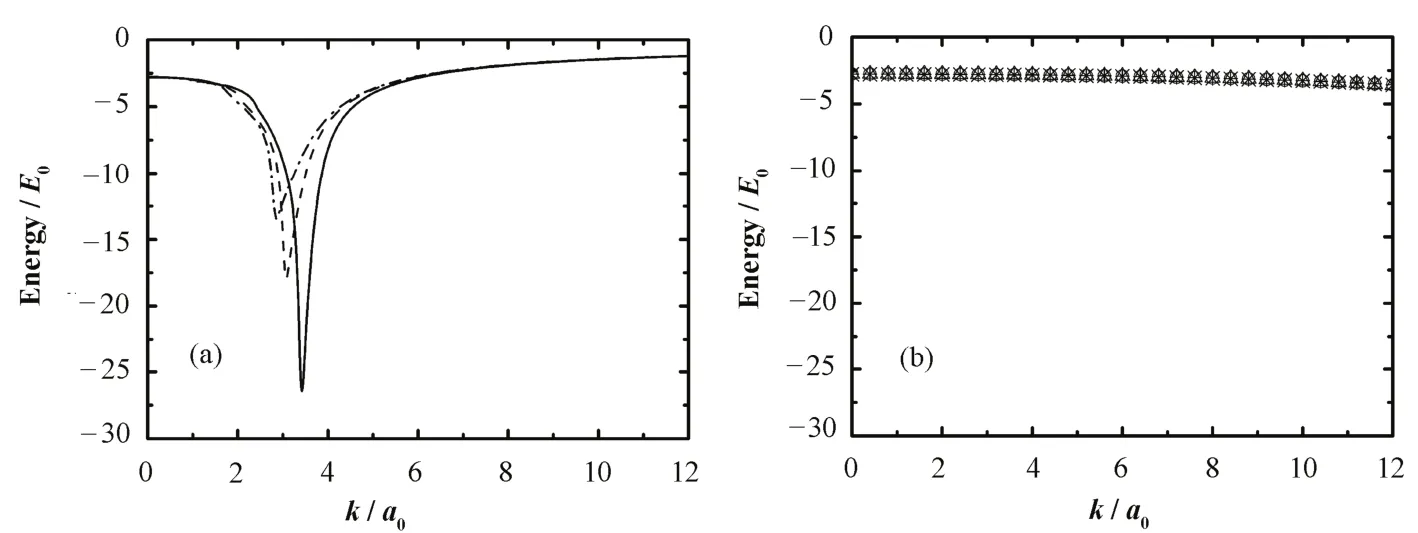
图4 动态PPA近似下T型量子线的电子(a)与空穴(b)的自能虚部Fig.4 The imaginary part of self energies of electron (a) and hole (b) of T-shaped quantum wire in dynamic PPA.—— Lx = Ly = 4(nm), - - - Lx = Ly = 7, −·−· Lx = Ly = 10

3 结语

采用有限温度下的格林函数理论计算了T型半导体量子线的载流子自能，采用包络线近似计算了各种截面尺度下的有效库仑势。为精确计算动态屏蔽效应，采用GW近似和PPA理论研究半导体量子线截面尺度的变化对能带能量的影响，并比较动态PPA理论和准静态PPA理论计算的能带能量。计算结果表明，准一维体系具有很强的量子限域效应，并显著增强了载流子间的有效库仑作用。受到电子间强烈散射的影响，动态屏蔽效应诱导了电子能带及寿命的很大变化。由于空穴具有较大的有效质量，动态屏蔽效应对其影响较小。

1 Haug H, Koch S W. Quantum theory of the optical and electronic properties of semiconductors[M]. Singapore: World Scientific, 2004

2 Hayamizu Y, Yoshita M, Takahashi Y, et al. Biexciton gain and the mott transition in GaAs quantum wires[J]. Phys Rev Lett, 2007, 99(16): 167403–167406

3 Someya T, Akiyama H, Sakaki H. Enhanced binding energy of one-dimensional excitons in quantum wires[J]. Phys Rev Lett, 1996, 76(16): 2965–2968

4 Yoshita M, Hayamizu Y, Akiyama H. Exciton-plasma crossover with electron-hole density in t-shaped quantum wires studied by the photoluminescence spectrograph method[J]. Phys Rev, 2006, B74(16): 165332

5 Wegscheider W, Pfeiffer L N, Dignam M M, et al. Lasing from excitons in quantum wires[J]. Phys Rev Lett, 1993, 71(24): 4071–4074

6 Akiyama H, Pfeiffer L N, Pinczuk A, et al. Observation of large many body coulomb interaction effects in a doped quantum wire[J]. Solid State Commun, 2002, 122(3–4): 169–173

7 Akiyama H, Yoshita M, Pfeiffer L N, et al. Onedimensional continuum and exciton states in quantum wires[J]. Appl Phys Lett, 2003, 82(3): 379–381

8 Akiyama H, Yoshita M, Pfeiffer L N, et al. Onedimensional excitonic states and lasing in highly uniform quantum wires formed by cleaved-edge overgrowth with growth-interrupt annealing[J]. J Phys: Condens Matter, 2004, 16(35): S3549–S3566

9 Itoh H, Hayamizu Y, Yoshita M, et al. Polarization dependent photoluminescence excitation spectra of one dimendisonal exciton and continuum states in T-shaped quantum wires[J]. Appl Phys Lett, 2003, 83(10): 2043–2045

10 Takahashi Y, Hayamizu Y, Itoh H, et al. Strong photoabsorption by a single quantum wire in waveguide transmission spectroscopy[J]. Appl Phys Lett, 2005, 86(24): 243101

11 Yoshita M, Liu S M, Okano M, et al. T-shaped GaAs quantum wire laser and the exciton mott transiton[J]. J Phys: Condens Matter, 2007, 19(29): 295217

12 Van der Meulen H P, Rubio J, Azcona I, et al. Optical emission of a one-dimensional electron gas in semiconductor V-shaped quantum wires[J]. Phys Rev, 1998, B58(16): 10705–10708

13 Sogawa T, Ando H, Ando S, et al. Interband optical transition spectra in GaAs quantum wires with rectangular cross sections[J]. Phys Rev, 1997, B56(4): 1958–1966

14 Bellessa J, Voliotis V, Grousson R, et al. High spatial resolution spectroscopy of a single V-shaped quantum wire[J]. Appl Phys Lett, 1997, 71(17): 2481–2483

15 Arakawa Y, Sakaki H. Multidimensional quantum well laser and temperature dependence of its threshold current[J]. Appl Phys Lett, 1982, 40(11): 939–941

16 Asada M, Miyamoto Y, Suematsu Y. Gain and the threshold of three-dimensional quantum-box lasers[J]. IEEE J Quantum Electron, 1986, 22(9): 1915–1921

17 Akiyama H, Pfeiffer L N, Pinczuk A, et al. Observation of large many body coulomb interaction effects in a doped quantum wire[J]. Solid State Commun, 2002, 122(3–4), 169–173

18 Duc H T, Tran Thoai D B. Low-temperature photoluminescence spectra of highly excited quantum wires[J]. Solid State Commun, 2003, 126(11): 645–648

19 Huai P, Ogawa T. Absorption and gain spectra of optically excited semiconductor quantum wires: effects of coulomb correlation and screening[J]. J Lumin, 2006, 119–120, 468–472

20 Huai P, Akiyama H, Tomio Y, et al. Coulomb enhancement and suppression of peak gain in quantum wire lasers[J]. Jpn J Appl Phys, 2007, 46(44): L1071–L1073

21 Benner S, Haug H. Plasma-density dependence of the optical spectra for quasi-one-dimensional quantum well wires[J]. Europhys Lett, 1991, 16(6): 579–583

22 Wang D W, Das Sarma S. Many body effects on excitonic optical properties of photoexcited semiconductor quantum wire structures[J]. Phys Rev, 2001, B64(19): 195313

23 Haug H, Schmitt-Rink S. Electron theory of the optical properties of laser-excited semiconductors[J]. Prog Quant Electr, 1984, 9(1): 3–100