基于小波和形态学结合的雷达图像降噪算法
赵松 李庆 江汉红 徐恒 雷明
(1. 海军工程大学电气与信息工程学院,武汉 430033;2. 武汉理工大学信息学院,武汉 430033;3 中国人民解放军91515部队)
0 引言
导航雷达是船舶进行导航、避碰的重要工具,随着计算机技术的不断发展,计算机技术嵌入式应用越来越广泛,计算机图形显示和图像处理技术日益成熟,采用图像处理的方法实现雷达目标的自动检测应运而生[1]。
导航雷达在工作过程中,受噪声和杂波影响,图像时常出现信噪比低、精度差的现象。对雷达图像进行数字图像预处理是进行目标跟踪、智能预警的基础,具有重要的意义。本文针对雷达图像目标和噪声特点,对小波与形态学的降噪方法深入分析研究,并根据实际应用环境提出了一种小波变换与形态学结合的降噪算法。
1 图像特点与降噪算法分割
1.1 雷达图像与噪声特点
导航雷达图像不同于合成孔径雷达(SAR),具有自身独有的特征。根据图1与图2可知,导航雷达成像为极坐标方式,图像相对简单,背景占较大面积,与目标之间灰度差别大,对应的图像直方图基本成单峰形状。单帧图像内,不同目标的亮度和形状可能会存在差异[1,2]。
雷达工作中,图像噪声干扰主要有系统噪声、环境杂波、人为干扰等。环境杂波数学模型复杂,主要通过信号处理进行抑制[2],系统噪声主要以传感器、电路产生的热噪声为主,具有时间上连续,振幅和相位随机的特点,可近似为白噪声。此外,雷达工作时存在部分脉冲噪声。

图1 导航雷达图像
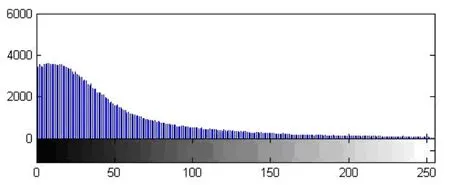
图2 图像1对应直方图
1.2 雷达图像的小波阈值降噪
小波分析是一门快速发展的时频信号处理技术,可以根据需要选取时间或连续频率的精度,被称为“数学显微镜”,具体原理见参考文献[3]。
小波去噪实际上是特征提取和低通滤波功能的综合[6]。图像经小波分解后,各个子频带具有不同的特性,噪声在高频段分布较多,同时在低频段中的噪声含量降低了许多。设图像为:
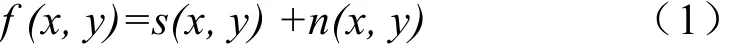
其中s、n分别代表有用信息与噪声,可知小波阈值降噪步骤如下:
1)对图像f (x, y)进行小波分解,获得低频小波系数h (x, y)和高频小波系数ω(x, y);
2)对高频系数进行阈值处理,获得阈值化后高频系数),(ˆyxω;
3)进行小波逆变换,利用阈值化后的小波系数重构图像,完成降噪过程。
1.3 形态学原理
数学形态学[9]是以集合运算为基础。在图像分割、降噪、边界提取、细化、粗化等图像处理中都设计应用。常用的数学形态学的基本运算主要有膨胀、腐蚀、开运算、闭运算、极限腐蚀、击中击不中变换、骨架抽取等,具体内容见参考文献[9],在此不赘述。
2 基于形态学小波运算的降噪算法
小波降噪对于高斯噪声具有较好的降噪效果,但对于脉冲噪声缺乏敏感性,国内外多名学者提出了不同的降噪改进算法,其中小波与形态学理论结合降噪[4,7-8]受到广泛关注。
对图像进行小波分解,得到高频小波系数,采用形态学算子对小波系数进行滤波,去噪时能够保留边缘性,对形态学变换后的小波系数进行软阈值处理,最终重构得到降噪后图像。
文献[4]利用水平线、垂直线与菱形算子处理小波分解后细节分量,文献[6]与[7]采形态学算法对小波降噪后图像平滑处理,文献[8]利用击中击不中变换处理系数矩阵,提高了微光、视频等图像的视觉效果。
小波分解后图像噪声存在于各细节分量中,因此本文对于分解系数矩阵采用形态学算子进行处理,采用矩形算子分别对水平、垂直、对角等细节分量进行处理。形态学处理运算矩阵如下:

采用闭运算对系数矩阵分别处理,处理公式为Y2=A·E,式中A为小波分解后系数矩阵,本文选取软阈值函数进行降噪处理。综上可得算法步骤:
1)对带噪雷达图像进行两层小波分解,计算小波分解系数;
2)提取不同类型的小波细节分量,对小波系数进行形态学开运算处理。
3)对形态学算子处理过的图像进行小波阈值处理,降噪函数选取为软阈值函数,门限设定为统一阈值。
4)用各层小波系数计算小波逆变换,重构图像,并计算信噪比。
3 仿真分析
利用Matlab环境,对信噪比为30.7553的雷达图像,采用小波阈值法、小波结合中值滤波降噪、文献[6]中算法及本文改进算法进行降噪仿真。降噪的客观质量用峰值信噪比(PSNR)来衡量。
小波基函数选取上,经大量实验验证降噪效果,bior2.4小波基以其良好的对称性、双正交性等特点,为降噪最优小波基,分解层数定为2层。降噪结果如图3至图7所示:

图3 原始图像

图4 小波阈值法降噪

图5 小波结合中值滤波降噪效果

图6 文献[6]中算法降噪效果

图7 本文算法降噪效果
从视觉效果看,小波结合中值滤波降噪后背景加深,文献[6]与本文改进算法视觉效果相似。
计算保留小数点后四位有效数字,可得实验峰值信噪比如表1所示。
通过图像对比,并综合对比降噪后信噪比数据可得以下结论:文献[6]中降噪算法效果一般,在雷达图像降噪中缺乏适应性;中值滤波结合小波降噪与本文方法降噪效果较好,本文改进算法效果最佳。
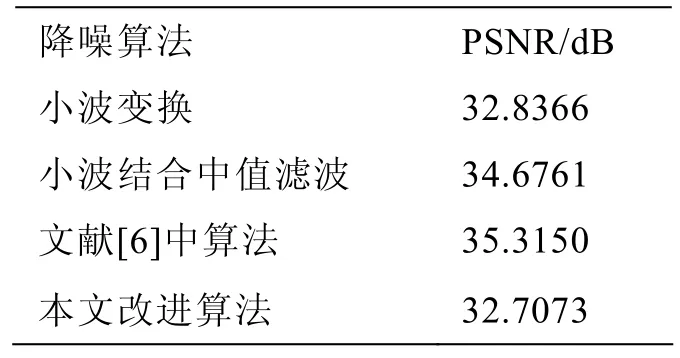
表1 不同方法降噪后的PSNR
4 结论
本文介绍了雷达图像的特征、小波变换及图像形态学的降噪的图像预处理方法,详细研究小波变换数学形态学相结合的改进算法。在此基础上,设计了小波形态学闭运算降噪方法,并借助Matlab环境对上述多种方法进行仿真验证。试验结果表明:优化算法优于普通的小波阈值法等多种算法,经预处理后的雷达图像峰值信噪比有一定提高,在雷达图像降噪中具有较好的应用前景。
[1] 李彤, 彭利文. 嵌入式计算机技术在雷达系统中的应用[J]. 计算机工程与科学, 2001,23(1): 75-81..
[2] 吴顺君, 梅晓春等. 雷达信号处理和数据处理技术[M]. 北京: 电子工业出版社, 2008.
[3] 崔锦泰, 程正兴. 小波分析导论[M]. 西安: 西安交通出版社, 1995: 67-88.
[4] Zhang Chaoliang, Jiang Hanhong, et al. Low light level image de-noising algorism based on wavelet transform and morphology[C]. 2009 International Conference on Computer Network and Multimedia Technology. WuHan: IEEE, 2009, 11: 307-310.
[5] 杨海丽. 小波变换在数字图像降噪处理中的应用[D].成都: 西南石油大学, 2007.
[6] 雷雁, 傅德胜. 一种基于形态学的小波自适应去噪算法[J]. 计算机工程, 2005, 31(18): 186-190.
[7] 王新智, 刘雨. 小波和形态学在雷达平面位置图像杂噪处理中的应用[J]. 光电与控制, 2003, 10(1):7-49.
[8] 候慧玲, 王明泉. 一种基于形态学的小波阈值去噪方法[J]. 图像处理, 2007, 23(43): 311-315.
[9] Richard A P. A new algorithm for image noise reduction using mathematical morphology[J]. IEEE Trans on Image Processing, 1995, 4(3): 542-548.

