随机共振在认知无线电频谱感知中应用的最新研究进展
邓 钦,万 频,王永华,李岳洪,杨 健
(广东工业大学 自动化学院,广州510006)
1 引 言
目前,无线通信技术在应用中面临着频谱资源严重匮乏的问题,主要原因不是频谱资源太少,而是频谱资源利用率过低[1]。认知无线电技术的出现,有效地解决了频谱资源“浪费”的问题。认知无线电的核心思想是允许认知用户(Secondary User,SU)在不对主用户(Primary User,PU)产生有害干扰的情况下动态地使用空闲的授权频段[2]。频谱感知是认知无线电的一项关键技术,它的主要功能在于检测可供认知用户使用的频谱空穴,以便认知用户能接入未使用的信道;同时监测主用户信号活动的情况,保证主用户再次使用该频段时,认知用户能够快速退出相应频段。
认知无线电频谱感知技术的研究主要集中在单节点感知(本地感知)和多节点协作感知[3]。单节点感知即单个认知用户对主用户的检测,包括能量检测、匹配滤波检测、循环平稳检测、自相关检测、协方差矩阵特征检测、干扰温度检测等;多节点协作感知即多个认知用户协作检测主用户信号,又可分为集中式感知和分布式感知。
在单节点感知技术中,能量检测的计算复杂度最低且容易实现,但是在低信噪比的环境下其检测性能会急剧降低[4];自相关检测具有与能量检测可比的计算复杂度,但是它在恒虚警概率的条件下检测性能低于能量检测器,原因是在主用户带宽多余时的非零滞后导致自相关系数趋于零[5];在循环自相关检测器中,必须估计循环频率以首先决定循环特征,这导致产生了比上述两种方法更大的计算复杂度[5];循环平稳检测利用统计特征进行信号识别,可区分信号和噪声,但是计算复杂度高,需要很高的抽样速率,并且抽样时钟偏移时影响检测性能[6];匹配滤波检测器是高斯白噪声信道下的最优检测器,但是它需要知道大量主用户的先验信息,而且对相位同步要求很高[7]。协作频谱感知技术能有效解决隐藏终端的问题,比单用户检测提高了检测概率,但是随着认知用户的增加,信道开销急剧加大,增加了计算的工作量,并有可能产生拥塞[8]。
认知无线电频谱感知中最大的挑战之一是如何对微弱频谱信号进行检测,换言之即怎样提高接收的频谱信号的信噪比(Signal-to-Noise Ratio, SNR)。低信噪比环境下频谱检测的性能会大幅降低,将随机共振(Stochastic Resonance, SR)引入到认知无线电频谱感知中可有效解决微弱信号检测问题。随机共振是物理中的一种非线性现象,在这种非线性的系统中可以通过在某种情况下加入合适的噪声以加强输出信号。其概念最初是由Benzi 等人[9]在研究古气象冰川问题时提出来的。近年来,随机共振被广泛应用在各种信号处理领域,如离散时间非线性AR模型[10]、信号检测器[11]等。随机共振描述了一个非线性系统与输入的信号和噪声之间存在某种匹配时,噪声能量就会向信号能量转移,输入信号的信噪比不仅不会降低,反而会增加,非常适用于弱信号的检测问题[12]。正因为随机共振的这种特性,可将它引入到频谱感知技术中,以提高感知性能。
目前,利用随机共振提升认知无线电频谱感知性能的研究还比较少,已有的研究主要集中在能量检测[13-19]、协方差矩阵检测[20]、循环平稳检测[21]和协作频谱感知[17-18,22-23]中,研究的方向主要可分为两类,一类是利用传统的双稳态随机共振作为系统模型以最大化提升信噪比来增强频谱感知性能;另一类是使用一种广义随机共振,不是最大化提升信噪比,而是以最优化检测性能为目的。下面将分别介绍随机共振在单节点和多节点感知技术中的应用,然后提出当前研究还有待解决的一些问题和一些新的看法,以期为随机共振在频谱感知中的应用研究提供一点借鉴。
2 随机共振
一个典型的离散过阻尼双稳态振荡器随机共振系统模型如下[24]:
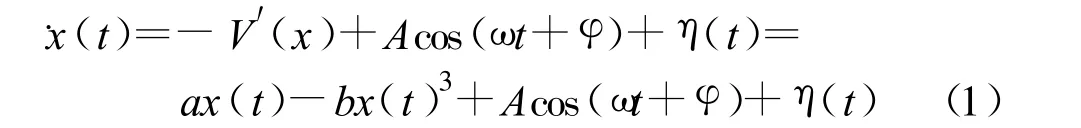
式中,A cos(ωt+φ)是输入信号;η(t)是引入的均值为0、方差为σ2η的随机共振噪声,且满足平均统计E[ η(t)η(t+τ)] =2Dδ(t -τ), 其中D 为噪声强度为映像对称平方势;a、b是该非线性系统的未知参数。
图1 中两个最低点x =±xm=± a/b 为该随机共振系统中的两个稳态点,或者称为势阱点,xb=0 是一个非稳态点,或者称势垒点。当仅有噪声时,质点以一定的周期在任一势阱点附近波动,当系统加入一个微弱的周期信号之后,由于周期信号的调制作用,系统的映像对称被打破了,质点在两个势阱之间做周期性波动。当质点从一个势阱跳到另一个势阱所需的平均时间是外力周期的一半时[13],将出现噪声、输入周期信号和质点运动同步的现象,有效抑制输出信号的噪声强度,使输出信号得到增强,即为随机共振。

图1 映像对称平方势的几何曲线图Fig.1 Geometric curve of image symmetrical square potential
3 随机共振在单节点感知技术中的应用
3.1 基于随机共振的能量检测
能量检测由于不需要知道主用户的任何先验信息及低的计算复杂度,被广泛应用在认知无线电频谱感知中。但是在信噪比较低的环境下,能量检测的性能会急剧下降,将随机共振系统引入到能量检测中可有效提高接收信号的信噪比,从而提高频谱感知性能。基于随机共振的能量检测模型可用图2表示。
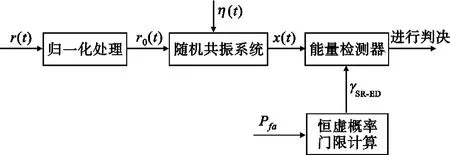
图2 基于随机共振的能量检测Fig.2 Energy detection based on SR
文献[13]将接收信号进行归一化处理后通过一个双稳态随机共振系统引入随机共振系统,将输出信号能量检测器进行判决,并假设通过随机共振系统前后接收信号的总能量不变。由于随机共振系统将一部分噪声能量转化为了信号能量,改变信号和噪声的比例,提高了信噪比,因此提升了能量检测器的检测性能。实验仿真表明,基于随机共振的能量检测在频谱感知性能上相对于传统的能量检测及自相关检测具有优越性。同时进行了计算复杂度的分析,提出的基于随机共振的方法和传统的能量检测方法在计算复杂度上相当。
文献[14]在文献[13]的基础上讨论了如何引入最优随机共振噪声σ2n0(opt)使输出信噪比最大化,并通过相关计算得到最优噪声σ2n0(opt)的表达式,频谱检测性能得到了进一步的提升。文献[14]指出:对于弱信号检测问题,若在两种假设情况(主用户存在与不存在)下的测试统计量能通过方差相同的一些高斯分布很好地逼近,则最优检测性能可以通过添加一个恒定的随机共振噪声到接收信号中并通过调整检测门限而得到。文献[14]给出了基于随机共振的具体的虚警概率和检测概率的理论表达式,与传统的能量检测方法进行理论和仿真的对比,得出在信噪比低于-10 dB时,基于随机共振的能量检测比传统的能量检测有更好的检测性能。
文献[15]提出使用随机共振滤波器应对频谱感知中弱信号检测的挑战,指出至少有两种主要方法用随机共振实现放大信号信噪比的功能,其一是固定随机共振系统参数并调整输入噪声的级别,其二是动态改变随机共振系统参数,但是执行情况要复杂得多,文献[15]采用了第一种方法。该文献讨论了两种基于随机共振的方法:Block Spectrum Sensing(BSS)及Sequential Spectrum Sensing(SSS)。BSS 方法使用一种特殊的随机共振系统将输入信号进行预处理,然后再用一个简单的能量检测器[25]进行判决,如图4 所示。

图3 随机共振作为能量检测器的预处理Fig.3 SR as a pre-treatment of the energy detector
SSS 方法监测主用户信号频率下的随机共振输出能量,并设置一个相关的水准E0。在快速变换检测中提出一种类似累积和的启发式算法[26-27],假设在第t 个FFT 窗口的检测能量为Et,则统计量可由下式得到:
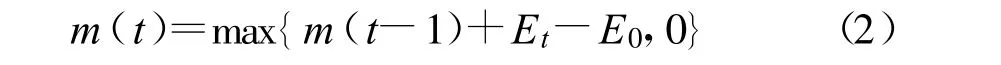
当m(t)>γ时,认为主用户出现;当没有主用户时,m(t)返回0 的概率很大。
对于一个特定的随机共振系统,在高信噪比环境下可能起不到提升检测性能的作用,文献[15]提出将单纯的能量检测与基于随机共振的能量检测进行并联,让检测性能在高信噪比和低信噪比的情况都能得到保证。随机共振系统通常只适合在低频率下的弱信号检测,即使可以将随机共振用于高频率的信号检测,硬件执行将会面临比低频率下更多的挑战,基于这一问题,文献[15]提供一条思路:使用一个固定频率的混频器和一个低通滤波器将高频信号转换为低频信号,但是硬件执行可能会面临更多的挑战。
通常,研究者们都是利用一个确定的随机共振系统来提升频谱感知性能,而且将检测性能的提升局限在仅提高信噪比上,但是信噪比并不总是直接反应了检测性能,譬如对一些非高斯信号而言,最大化其输出SNR 并不表示着其检测性能为最优。文献[16-17] 针对这些问题进行了改进,提出了新的基于随机共振的感知方案:首先是应用了一种广义的随机共振检测器[28-32],可适用于任何非线性系统;其次,在恒虚警概率情况下,不是最大提高信号信噪比,而是以最优化检测性能为目的。该文献将主用户信号假设成一个常量A,推导出检测概率表达式为
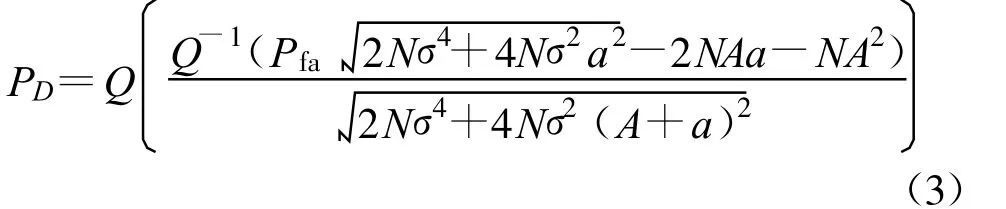
然后通过实验观察得到最优参数a,使检测概率最大,即aopt=arg max a (PD)。
信噪比墙对能量检测器的应用具有重要的指导意义。当信噪比接近于信噪比墙时,采样复杂度将会趋于无穷大。当信噪比低于信噪比墙时,误检率将会增加50%以上[33],检测性能会急剧下降。文献[18]提出通过将接收信号作为驱动信号引入到混沌随机共振(Chaotic Stochastic Resonance,CSR)系统,不仅提高了原接收信号的信噪比,达到降低信噪比墙的目的,同时在相同的恒虚警概率和检测概率需求的情况下降低了信号的采样复杂度。在仅有能量检测的情况下,采样数N 可表示如下:
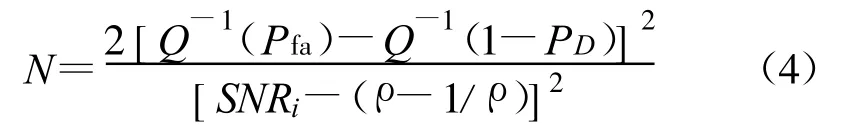
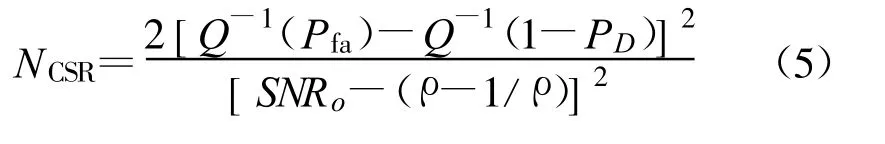
由于N CSR-N<0,说明采用基于混沌随机共振的能量检测其采样复杂度降低了,基于CSR 方法的信噪比墙:
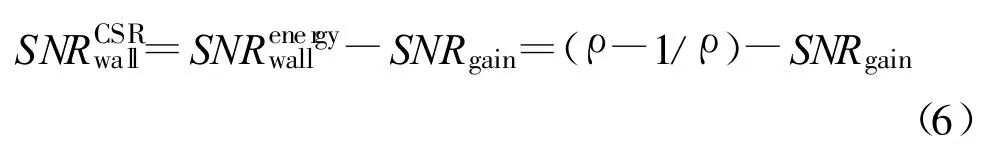
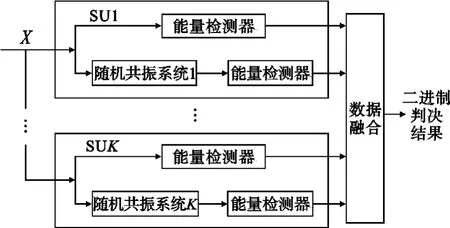
很明显SNRCSRwall 鉴于通常都是研究高斯噪声背景下的频谱感知性能,文献[19]研究了色噪声背景下基于随机共振的频谱感知性能,在低信噪比的各种不同的色噪声背景下,基于随机共振的能量检测器性能优于传统能量检测器。 文献[20]在一种基于接收信号协方差矩阵的频谱感知算法——协方差绝对值(Covariance Absolute Value,CAV)算法[34-35]的基础上加入一种广义的随机共振[28-32],基于Neyman-Pearson 准则,在保持虚警概率恒定的情况下,在主用户信号存在和不存在两种情况下通过加入特定信号使检测统计量的概率密度函数(PDF)最大化,实现在极低信噪比环境下大幅提高协方差矩阵频谱感知算法的检测性能。为了使所提出算法的检测性能最优,需加入一个最优随机共振噪声,其概率密度函数的形式为[31] 由于同时求解最优参数λ、n1、n2难度很大,文献[20]改用a 来代替n1、n2,转为求解次优的简化噪声。计算出使检测概率最大化的a 的表达式,通过数值计算得到检测概率pd和a 的关系图,根据关系图选择最优的随机共振参数a,最终计算出检测概率的值。通过实验仿真发现,基于随机共振的协方差矩阵频谱感知算法在很低信噪比环境下可以显著提高频谱感知性能,同时可大幅节省感知时间,且计算复杂度也小于协方差矩阵感知算法。 匹配滤波器是最优检测器,但它需要知道主用户的先验信息,同时对相位的同步要求高;能量检测实现简单,但它不能区分信号和噪声及难以设定判决门限。循环平稳特征检测克服了上述两种方法的缺点,可以区分调制信号和噪声,并且针对不同的循环频率还能区分调制信号和干扰信号的类型,在低信噪比情况下仍然具有较高的检测性能[36]。文献[21] 提出将随机共振(SR)与循环平稳特征检测(CFD)相结合,以进一步提高检测性能,系统模型如图4 所示。 图4 基于随机共振的循环平稳特征检测Fig.4 Framework of the spectrum sensing method based on CFD with SR 隐藏终端问题是频谱感知的又一大挑战,利用多节点协作频谱感知技术可以有效地解决隐藏终端问题。首先各本地节点先独自作检测,然后将检测结果发送到融合中心作全局判决,通过这样多个节点的协作判决可降低因个别认知用户漏检而产生的干扰概率。协作感知按判决融合算法可分为硬合并和软合并两种。在硬合并中常见的算法有“与”准则、“或”准则和K 秩序准则等,在软合并中常见的算法有等增益合并(Equal Gain Combination,EGO)、最大比值合并(Maximal Ratio Combination, MRC)和选择式合并(Selection Combination, SC)3 种方式。 文献[17-18]主要分析随机共振原理应用于协作感知中的软合并,指出了基于随机共振协作检测提高协作感知的感知性能的两种途径。一种是在各本地节点引入随机共振系统,改变各本地节点所接收到信号的统计量,再一起送往融合中心作判决,该方法以提高本地节点检测性能从而提高协作感知的整体性能;另一种是在各本地节点将观察数据送往融合中心后加入SR 噪声,通过改变融合中心处本地节点所传送过来的检测统计量值,使其分布发生改变来提高协同感知的性能。文献[17-18]采用了最大比合并(MRC)和等增益合并(EGC)这两种线性合并算法来讨论其SR 协作算法的性能,通过最优化一个参数,使检测概率达到最大,证明基于随机共振的MRC 和EGC 方法在检测性能上得到了改善。还指出对于线性融合,用添加随机共振噪声的方法不能提高其检测性能。 文献[22]提出一种基于随机共振的审查协作感知方法,与基于随机共振的能量检测协作感知方法相比,在拥有相同的检测性能的前提下大大降低了计算复杂度。该方法采用双门限λ1和λ2,当测试统计量Ti <λ1 时,认为主用户不存在;当Ti ≥λ2时,认为主用户一定存在,即检测概率为1;当λ1 文献[23]在传统的协作频谱感知基础上,加入了随机共振系统,并将提出的基于随机共振的协作感知方法与非协作的能量检测、协作的能量检测,随机共振噪声为正态分布、韦伯分布、正态对数分布的随机共振能量检测进行了性能的比较,实验证明提出的方法感知性能明显优于其他几种方法。所提出方法的独特之处在于:在传统的基于随机共振测试统计量基础上,为了简化融合后的过程及保持与能量检测相同的门限,将A(x)与一个常数γED/γSR-ED相乘得到一个新的测试统计量,并将基于测试统计量A(x)的传统能量检测与基于测试统计量B(x)的随机共振能量检测相结合用在每个认知用户中。让每个认知用户的随机共振系统均相同,而根据噪声类型的不同引入的随机共振噪声均不相同,利用贝叶斯融合方法对检测性能进行比较分析。所提出方法的方框图如图5 所示。 图5 随机共振能量检测器的协作频谱感知方框图Fig.5 Block diagram of the proposed cooperative sensing approach based on SR energy detector fusion 以上综述了随机共振在认知无线电频谱感知技术的应用,通过随机共振系统,将噪声有效利用起来,可以提高接收信号SNR,进而提高频谱感知性能。但是基于随机共振的认知无线电频谱感知研究中还存在一些问题有待于进一步的研究:第一,目前大部分研究仅仅是利用随机共振最大化提升接收信号的信噪比为目的,但是对于一些非高斯信号,信噪比并不总是直接反应了检测性能;第二,随机共振检测器中的非线性系统都是固定的,多数是由朗之万方程决定的,对随机共振在认知无线电频谱感知的应用造成了一定的限制;第三,随机共振系统通常适用于低频下的弱信号检测,即使能用在高频环境下,硬件执行将面临更大的挑战,文献[15]提出使用低通滤波器将高频信号转换为低频信号,具体怎样实施有待于进一步研究;第四,引入的随机共振系统应满足哪些条件,系统参数如何设置,随机共振噪声如何确定,已有的文献也未进行相关说明;第五,对于噪声不确定情况下的基于随机共振的认知无线电频谱感知应用,也是值得进一步考虑的。 针对上述问题,在频谱感知中利用随机共振的进一步研究应该集中在:如何利用随机共振在不同的信道或不同的背景噪声下提升检测性能;利用一些非传统随机共振系统,如单稳态、多稳态随机共振;如何利用随机共振提升高频信号的频谱感知性能。 尽管还面临着诸多的技术挑战,但随着随机共振在认知无线电频谱感知中的应用研究的不断深入,相信在不久的将来,随机共振将会为认知无线电频谱感知带来新的动力和契机。 [ 1] FCC 02-155,Spectrum Policy Task Force Report[S] . [ 2] Xu Yi, Wang Rui, Wang Fei.Detection of Ampl-itudevaried Weak Signal by Genetic Adap tive Stochastic Resonance Algorithm[C]// Proceedings of the Eighth International Conference on Electronic Measurement and Instruments.Hefei,China:IEEE, 2007:626-630. [ 3] Akyildiz Ian F, Lee Won-Yeol, Vuran M C, et al.Next Generation/Dynamic Spectrum Access/Cognitive Radio Wireless Networks:a Survey[ J] .Computer Networks, 2006, 50(9):2127-2159. [ 4] Digham F F, Alouini M S, Simon M K.On the energy detection of unknown signals over fading channels[J] .IEEE Transactions on Communications,2007,55(1):21-24. [ 5] Ikuma T,Nagaghi-Pour M.A comparison of three classes of spectrum sensing techniques[ C]//Proceedings of Global Telecommunications Conference.New Orleans, LO:IEEE,2008:1-5. [6] Tkachenko A, Cabric D, Brodersen R W.Cyclostationary feature detector experiments using reconfigurab le BEE2[C]//Proceedings of 2nd IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks.Dublin, Ireland:IEEE,2007:216-219. [7] 刘子琦,冯春燕,曾志民等.认知无线电网络中物理层频谱检测算法的研究[J] .电信科学,2009,25(3):64-69. LIU Zi-qi, FENG Chun-yan, ZENG Zhi-min, et al.Study on Spectrum Sensing Algorithms of Physical Layer in Cognitive Radio Network[ J] .Telecommunications Science,2009, 25(3):64-69.(in Chinese) [8] Lunden J, Koivunen V, Huffunen A, et al.Colla borative cyclostationary spectrum sensing for cognitive radio systems[J] .IEEE Transactions on Signal Processing, 2009, 57(11):4182-4192. [9] Benzi R,Sutera A, Vulpiani A.The mechanism of stochastic resonance[J] .Journal of Physics A:Mathematical and General, 1981, 14(11):453-457. [10] Zozor S, Amblard P O.Stochastic resonance in discrete time nonlinear AR(1)models[ J] .IEEE Transactions on Signal Processing, 1999, 47(1):108-122. [11] Zozor S, Amblard P O.Stochastic resonance in locally optimal detectors[ J] .IEEE Transactions on Signal Processing,2003, 51(12):3177-3181. [12] Zhao Zhijin, Yao Yao, Xu Chunyun.A Time-Frequency Analysis Method Using Stochastic Resonance[ C]//Proceedings of 2008 International Conference on Image and Signal Processing.Sanya,China:IEEE,2008:569-572. [13] He Di.Improving the Spectrum Sensing Performance in Cognitive Radio Networks Using the Stochastic Resonance Approach[C]// Proceedings of 2009 Asia Pacific Conference on Postgraduate Research in Microelectronics &Electronics.Shanghai:IEEE, 2009:283-286. [14] He Di, Lin Yingpei, He Chen, et al.A Novel Spectrum-Sensing Technique in Cognitive Radio Based on Stochastic Resonance[ J] .IEEE Transactions on Vehicu lar Technology, 2010,59(4):1680-1688. [15] Zheng Kun, Li Husheng, Djouadi S M, et al.Spectrum Sensing in Low SNR Regime Via Stochastic Resonance[ C]//Proceedings of 2010 44th Annual Conference on Information Sciences and Systems.Princeton, NJ:IEEE,2010:1-5. [16] Chen Wei, Wang Jun, Li Husheng, et al.Stochastic Resonance Noise Enhanced Spectrum Sensing in Cognitive Radio Networks[C]// Proceedings of 2010 IEEE Global Telecommunications Conference.Miami,FL:IEEE,2010:1-6. [17] 陈伟.认知无线电中的频谱感知与干扰评估技术研究[ D] .成都:电子科技大学,2007. CHEN Wei.A Research on Spectrum Sensing and interference estimation in Cognitive Radio Networks[ D] .Chengdu:University of Electronic Science and Technology of China,2007.(in Chinese) [18] He Di.Breaking the SNRWall of Spectrum Sensing in Cognitive Radio by Using the Chaotic Stochastic Resonance[C]// Proceedings of 2010 International Conference on Circuits and Systems.Paris:IEEE, 2010:61-64. [19] He Di, He Chen,Jiang Lingge, et al.Spectrum Sensing Ap-proach Based on Optimal Stochastic Resonance Technique under Color Noise Background in Cognitive Radio Networks[C]//Proceedings of 2010 IEEE International Conference on Communications.Cape Town,South Africa:IEEE,2010:1-4. [ 20] 张少文,王军, 陈伟,等.一种基于随机共振增强的协方差矩阵频谱感知算法[J] .信号处理, 2011,27(11):1633-1639. ZHANG Shao-wen, WANG Jun, CHEN Wei, et al.A Spectrum Sensing Algorithm Based on Sto- chastic Resonance Enhanced Covariance Matrix Detection[ J] .Signal Processing, 2011, 27(11):1633-1639.(in Chinese) [ 21] Lin Yingpei, He Chen, Jiang Lingge, et al.A Cyclostationary-Based Spectrum Sensing Method Using Stochastic Resonance in Cognitive Radio[ C]//Proceedings of 2010 International Conference on Communications.Cape Town,South Africa:IEEE,2010:1-5. [22] Lin Yingpei, He Chen, Jiang Lingge, et al.A Censoring Cooperative Spectrum Sensing Scheme Based on Stochastic Resonance in Cognitive Radio[ C]//Proceedings of 2011 International Conference on Communications.Kyoto:IEEE,2011:1-5. [ 23] He Di, Jiang Lingge.Cooperative Spectrum Sensing Approach Based on Stochastic Resonance Energy Detectors Fusion[ C]//Proceedings of 2011 International Conference on Communications.Kyoto:IEEE,2011:1-5. [ 24] Luea Gammaitoni, Perter Hanggi, Peter Jung, et al.Stochastic Resonance[ J] .Reviews of Modem Physics,1998,70(1):223-287. [ 25] Cordeiro C, Ghosh M, Cavalcanti D, et al.Spectrum sensing for dynamic spectrum access of TV bands[ C]//Proceedings of the 2nd International Conference on Cognitive Radio Oriented Wireless Networks and Communications.Orlando,FL,USA:IEEE, 2007:225-233. [ 26] Poor H V, Hadjiliadis O.Quickest Detection[ M] .England:Cambridge University Press,2008:175-189. [ 27] Lai Lifeng, Fan Yijia, Poor H.V.Quickest detection in cognitive radio:A sequential change detection framework[C]// Proceedings of 2008 IEEE Global Communication Conference.New Orleans,LO:IEEE, 2008:1-5. [ 28] Steven K.Can Detectability Be Improved by Adding Noise?[ J] .IEEE Signal Processing Letters,2000, 7(1):8-10. [ 29] Steven K, Michels J H, Chen Hao, et al.Reducing Probability of Decision Error Using Stochastic Resonance[ J] .IEEE Signal Processing Letters, 2006, 13(11):695-698. [ 30] Kay S.Noise Enhanced Detection as a Special Case of Randomization[ J] .IEEE Signal Processing Letters, 2008, 15(1):709-712. [ 31] Chen Hao, Varshney P K, Kay S M, et al.Theory of the stochastic Resonance Effect in Signal Detection:Part IFixed Detectors[ J] .IEEE Transactions on Signal Processing, 2007, 55(7):3172-3184. [32] Chen Hao, Varshney P K, James H.Michels, et al.Approaching Near Optimal Detection Performance via Stochastic Resonance[ C]//Proceedings of 2006 IEEE International Conference on Acoustics, Speech and Signal Processing.Toulouse:IEEE,2006:281-284. [33] Tandra R, Sahai A.SNR walls for signal detection[ J] .IEEE Journal of Selected Topics in Signal Processing, 2008,2(1):4-17. [34] Zeng Y, Liang Y C.Covariance Based Signal Detections for Cognitive Radio[ C]// Proceedings of New Frontiers in Dynamic Spectrum Access Networks.Singapore:IEEE, 2007:202-207. [35] Zeng Y, Liang Y C.Spectrum sensing algorithms for cognitive radio based on statistical covariances[ J] .IEEE Transactions on Vehicular Technolgy, 2009, 58(4):1084-1815. [36] 张昊晔, 包志华.基于循环平稳特征的频谱检测[ J] .通信技术,2010,43(9):41-45. ZHANG Hao -ye, BAO Zhi -hua.Spectrum Sens ing Based on Cyclostationary Characteristics[ J] .Communications Technology, 2010, 43(9):41-45.(in Chinese)3.2 基于随机共振的协方差矩阵频谱感知
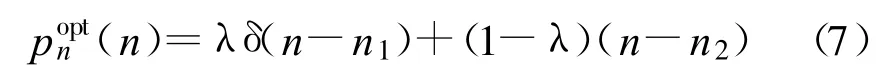
3.3 随机共振用于循环平稳特征检测

4 随机共振应用于多节点协作频谱感知
4.1 协作频谱感知
4.2 随机共振应用于协作频谱感知的相关研究
5 结 语

