一种改进的认知域自适应干扰温度估算算法
刘 伟,王红军,张旻
(解放军电子工程学院, 合肥230037)
1 引 言
认知无线电[1-2]是一种能够与其操作环境进行交互进而改变传输参数的新型无线电,能够通过频谱感知搜索频谱空穴动态地利用频谱[3-5],并且在主用户的再次出现,实现主动规避,从而不影响其他用户的工作。美国联邦通信委员会(FCC)在2002 年针对认知无线电的需求提出了“干扰温度”的概念,将“干扰温度”定义为衡量授权用户接收机所受到干扰的标准。当电磁环境里不存在通信用户的信号时,干扰温度主要来自基底热噪声。“干扰温度限”则被定义为在最初噪声基准的基础上,授权用户接收机所能够容忍的由于认知用户加入而带来的干扰能量提高的最高程度,用来表明某应用场景里特定工作频段内满足接收要求的最差无线传输环境,认知用户累积干扰只要不超过干扰温度限,就可以共享使用该频谱工作。当有通信用户出现时,无论授权用户还是认知用户的发射信号都会导致干扰温度升高。因此,通过对“干扰温度”的估算,并将其与“干扰温度限”进行比较,就可以得到未知电磁环境下频谱利用概况,作为是否能够通信的依据。
关于干扰温度的测量,基于多窗口谱估计(Multi-taper Method,MTM)联合奇异值分解(Singular Value Decomposition,SVD)的算法为当前次最优干扰温度估计方法[6-8]。Haykin S 为实现干扰温度估计,提出了如下两点假想[1]:设想采用较大数量的传感器,将传感器分布在待查的区域内,用以克服不同空间位置上电磁环境的空间差异;基于这种多传感器的思想,采用多窗口谱估计联合奇异值分解(即MTM-SVD 算法)来进行干扰温度的谱估计。多窗口谱估计算法是使用多个Slepian 序列作为正交窗函数,Slepian 序列的显著特性是在采样点有限时的傅氏变换具有极佳的能量集中特性。这种特性允许折衷谱分辨率来改善谱特性,使得在降低谱估计的方差时不会影响估计偏差。将每个Slepian 序列都应用于整个记录数据并采用快递傅里叶变换计算周期图,最后对周期图平均就得到相应的谱估计。
很多研究都采用MTM-SVD 算法进行干扰温度估计[9-12],文献[9]局部改进了SVD 算法,减少了计算量,实时性较好,但引入了噪声。文献[10-11]采用压缩感知降低了采样速率,检测性能与经典中MTM-SVD 算法相当。文献[12] 基于MTM -SVD算法,结合干扰源数量、位置和功率进行了频谱感知,但没有进行降噪处理。本文针对上述算法中仅采用奇异值分解难以起到降噪作用的不足,采用了基于自适应谱线增强技术对MTM-SVD 算法进行了改进(改进算法简称为ALE-MTM-SVD),极大地提高了干扰温度估算性能。
2 基于自适应谱线增强技术的MTM-SVD算法
干扰温度在认知域用来度量干扰(含噪声)功率和所占的带宽大小:

式中,Tl(fc,B)为噪声温度,Pl(fc,B)为带宽为B 、频点fc 处干扰的平均功率,k 为玻耳兹曼常数。因此,干扰温度可以看作是特定工作频段内的干扰功率谱密度。
干扰温度估算算法模型如图1 所示。

图1 干扰温度估算模型Fig.1 The model of interference temperature estimation
数据来源为预置或投放到一定区域内的探测传感器。传感器首先通过宽带接收模块完成指定频率范围内信号接收,通过A/D 得到量化的时间序列,该时间序列用来进行干扰温度估算,估算算法主要分为两步:时间序列自适应谱线增强降噪和权值变量求解、干扰温度估计。下面就估算算法的两个核心内容进行阐述,并对功率谱与干扰温度之间关系进行了推导。
2.1 自适应谱线增强算法
为了进一步提高估计性能和抑制权系数噪声,利用自适应谱线增强器进行改进,自适应谱线增强算法的设计如图2 所示。图中,ΔT 为延时线,T 为采样周期,设接收到的时间序列为x(n)。为了使延时后的x(ΔT)与噪声互不相关,ΔT 应大于噪声的时间相关半径。由于自适应谱线增强器抵消了x(n)和x(ΔT)中的干扰分量,X1(n)中的目标信号得到了进一步突显,使得X1(n)信噪比得到了有效提高。
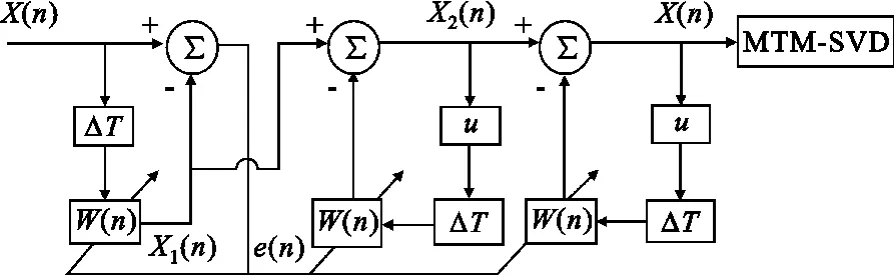
图2 ALE 谱线增强算法Fig.2 Adaptive line enhancement algorithm
首先进行第一级输出X1(n)的推导,ALE 的原始输入信号为

经过延时后信号为
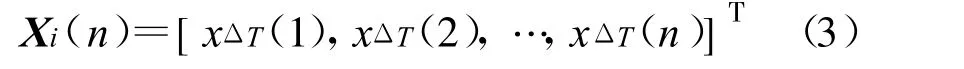
选取LMS 自适应滤波器的阶数为M,则n 时刻滤波器输入信号向量和权向量分别为
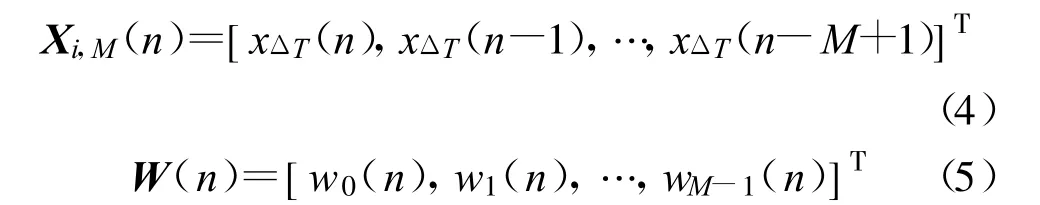
该时刻滤波器的输出为
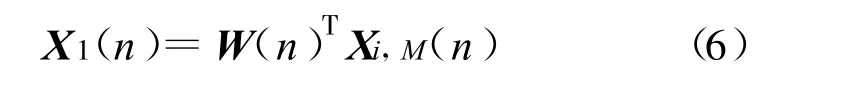
基于最速下降法的LMS 算法迭代公式为
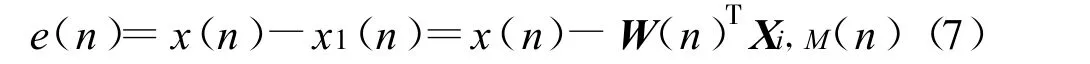
权值变量wi更新方程可表示为
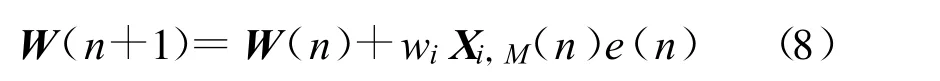
由此可得第一级输出为
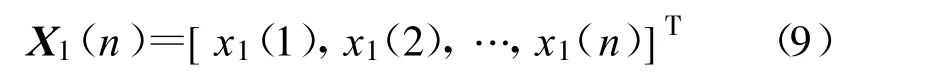
采用瞬间误差平方是均方误差的一种较好估计,故采取的策略为尽可能地减小瞬间误差平方。瞬间误差平方表达式如下:
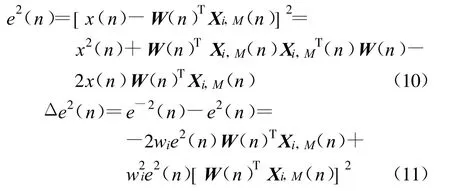
为尽可能地减小瞬间误差平方,应选择合适的wi,使Δe2(n)为尽可能小的负值,故有:
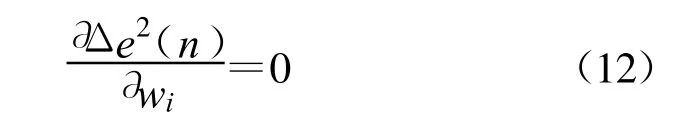
经推导得:
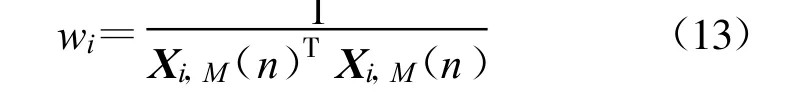
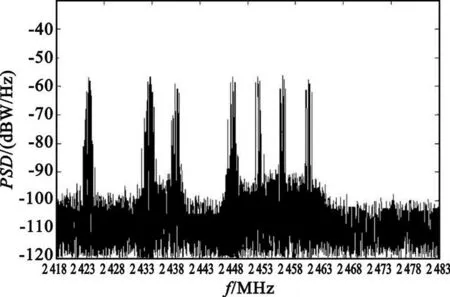
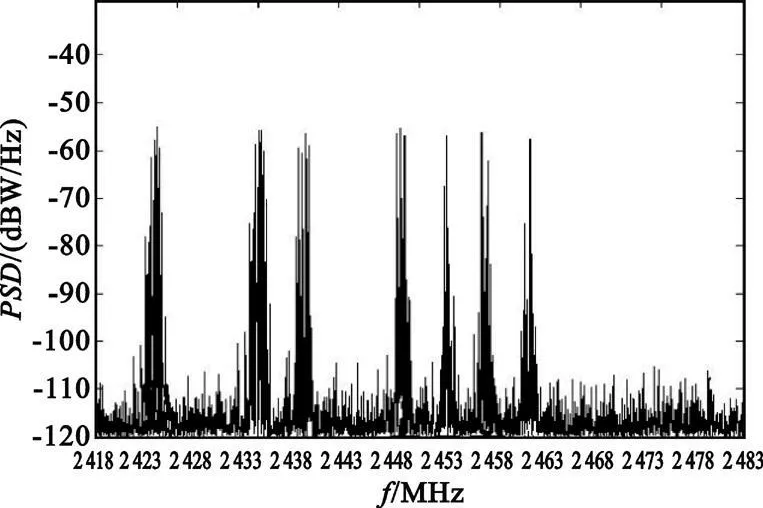
为预防控制失调,权值变量wi需引入固定步长参数w0,0 权向量更新公式因此变为 图2 后两级累加器的参数ΔT、W(n)和wi与第一级累加器取相同参数值。因此,对目标信号来说,累加器实质是2π整数倍的移相器,即在累加过程中信号分量是同相相加,而干扰分量只是能量大小简单求和,系统增益得到明显提高。 在上述自适应谱线增强算法中, W(n)迭代算法所占计算量的比例是最大的,是整个算法的运算量所在,但由于累加器的W(n)在第一步推导中已经求出,所以在实际运用中,与普通一级ALE 谱线增强器相比计算量增加并不多。 通过上述推导,可得相应的特征谱为以下傅里叶变换形式: 其中, SmNm=1表示与传感器设置地点有关的权值变量,是正交Slepian 序列;Y(m)k 表示第m 个传感器通过计算得到的第k 个特征谱;N 表示传感器的个数;K 表示所选择的Slepian 序列的个数。将得到的特征谱排列为公式(18)的形式: 矩阵A(f)中的每个元素都与加性噪声和接收到的信号有关。算法主要对信号进行奇异值分解进行干扰温度估计。σ0(f), σ1(f), …, σN(f)为矩阵A(f)的奇异值。 再进行如下推导: 由此可得出结论: 选取矩阵A(f)AT(f)所有奇异值的平方和σ21(f)+σ22(f)+…+σ2r(f)作为频率点f 的干扰温度估计值。 在求解干扰温度后,为了明确干扰温度估计值与功率谱之间的关系,利用MTM 算法进行功率谱估计: 其中: 为第i 个传感器接收信号的MTM 算法功率谱估计,λk≈1,k =1,2, …,K。 因此,可以得到干扰温度估计值与功率谱的关系公式为 以家庭无线AP 的室内环境为应用场景, 符合IEEE 802.11G 标准,工作在2.4 GHz, 调制样式为256QAM,仿真时以无线AP 的下行13 个信道随机占用进行干扰温度估算,通过对干扰温度分布图的比较来评估ALE-MTM-SVD 与MTM-SVD 算法的性能,限于篇幅,仅给出占用6 个信道时的仿真图,信道分布如表1 所示。仿真采用蒙特卡洛法,噪声为高斯白噪声,采用(0,1)分布模型。 表1 信道占用情况Table 1 The condition of the channel occupancy 仿真分为两步:没有用户进行通信时原始噪底估算和有用户通信情况下的干扰温度估计。图3 为Matlab 采用白噪声后得到的原始噪底仿真结果图,噪底约为-118 dBm。 图3 原始噪底仿真图Fig.3 The original noise floor 图4 和图5 分别为ALE-MTM-SVD 和MTMSVD 算法的干扰温度仿真结果图。 图4 MTM-SVD 干扰温度分布图Fig.4 Interference temperature of MTM-SVD 图5 ALE-MTM-SVD 干扰温度分布图Fig.5 Interference temperature of ALE-MTM-SVD 从图4 和图5 不难看出:MTM-SVD 算法虽然能够检测到信号功率谱峰值,但由于噪声抑制能力差,信道相邻近时检测带宽内整体噪底被抬高。ALE-MTM-SVD 与MTM-SVD 相比有效地抑制了噪声,在噪底没有被抬高的情况下显著地突出了功率谱峰值,提高了干扰温度估算的精度和可信度,可以为认知通信寻求频谱空穴提供一个通信的依据,也为干扰回避和功率控制提供了基础。 本文针对异常复杂瞬息多变的无线频谱应用状况,提出了一种改进干扰温度MTM -SVD 估算算法,一方面保证了MTM 谱估计算法近最优性的特点,实现对无线频谱是否可用或是否存在干扰有一个准确而及时的认知;另一方面通过降噪处理和权值求解,得到了干扰温度与功率谱之间的准确对应关系,对干扰温度估算更为准确,且能够实时地反映无线频谱的变化,基本满足实际应用的要求。 [ 1] Haykin S.Cognitive radio:brain-empowered wireless communications[ J] .IEEE Journal on Selected Areas in Communications, 2005,23(2):201-220. [ 2] Stevenson C, Chouinard G,Lei Zhongding, et al.IEEE 802.22:The first cognitive radio wireless regional area network standard[ J] .IEEE Communications Magazine, 2009, 47(1):130-138. [3] Hussain S, Fernando X.Spectrum sensing in cognitive radio networks:Up -to-date techniques and future challenges[C]//Proceedings of 2009 IEEE Toronto International Conference on Science and Technology for Humanity.Toronto,Canada:IEEE,2009:736-741. [ 4] Xing Yiping, Chandramouli R, Mangold S.Dynamic spectrum access in open spectrum wireless network[ J] .IEEE Journal on Selected Areas in Communications,2006,24(3):626-637. [ 5] Yucek T, Arslan H.A survey of spectrum sensing algorithms for cognitive radio applications[ J] .Communications Surveys&Tutorials, 2009,11(1):116-130. [ 6] Bronez T P.On the performance advantage of multitaple spectral ananlysis[J] .IEEE Transactions on Signal Processing,1992,40(12):2941-2946. [ 7] Walden A T, Mccoy E, Percival D B.The variance of mu ltitaple spectrum estimates for real gussian processes[J] .IEEE Transactions on Signal Processing, 1994,42(2):479-482. [ 8] Riedel K S, Sidorenko A.Minimum bias multiple taper spectral estimation[ J] .IEEE Transactions on Signal Processing,1995, 43(1):188-195. [9] Zhao Bing, Guo Lili.Research of Spectrum Detection Technology in Cognitive Radio[C]//Proceedings of 2009 International Conference on Networks Security, Wireless Communications and Trusted Computing.Wuhan:IEEE,2009:188-191. [10] Zhao Linjing, Chen Xi, Zhang Gangshan.A Novel Spectrum Sensing Algorithm Based on Compressive Sensing for Cognitive Radio[ C]//Proceedings of 2011 IEEE International Conference on Advanced Information Networking and App lications.Biopolis:IEEE,2011:243-246. [11] Jiang Ting, Zhai Shijun .The Wideband Spectrum Sensing Based on Compressed Sensing and Interference Temperature Estimation[C]//Proceedings of the 5th International Conference on Wireless Algorithms, System s, and Applications.Beijing:IEEE,2010:344-352. [12] Zhang Yi, Xue Zhe, Zhang Xikai.An improved united domain spectral analysis in cognitive radio[ C]//Proceedings of 2010 International Conference on Computer Application and System Modeling.Taiyuan:IEEE, 2010:652-655.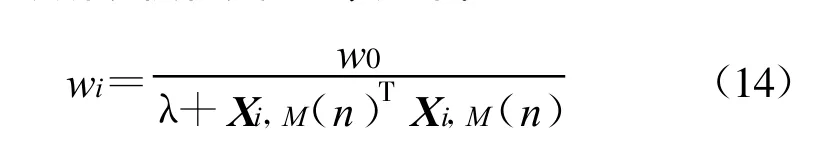
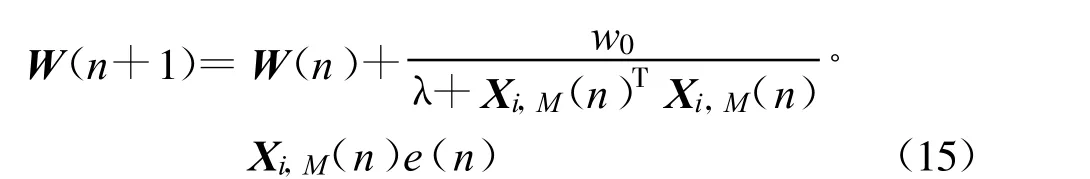
2.2 干扰温度估算算法
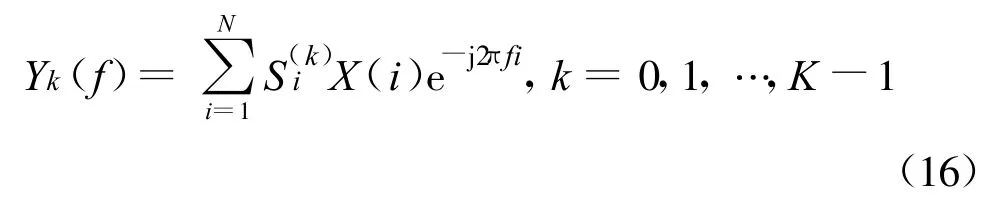

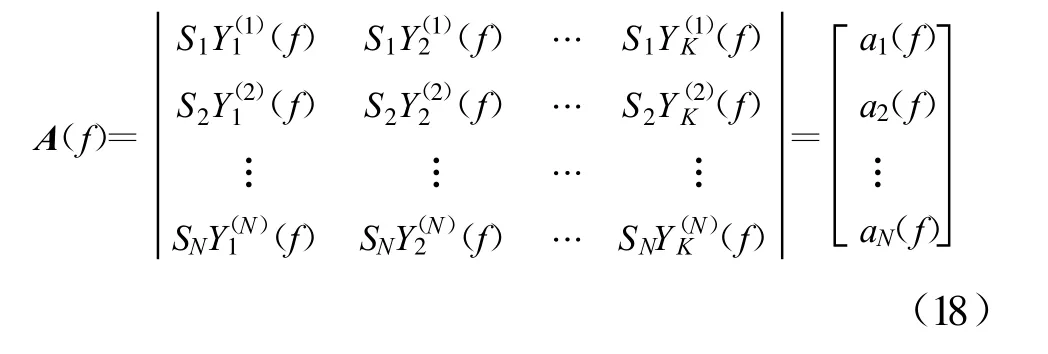
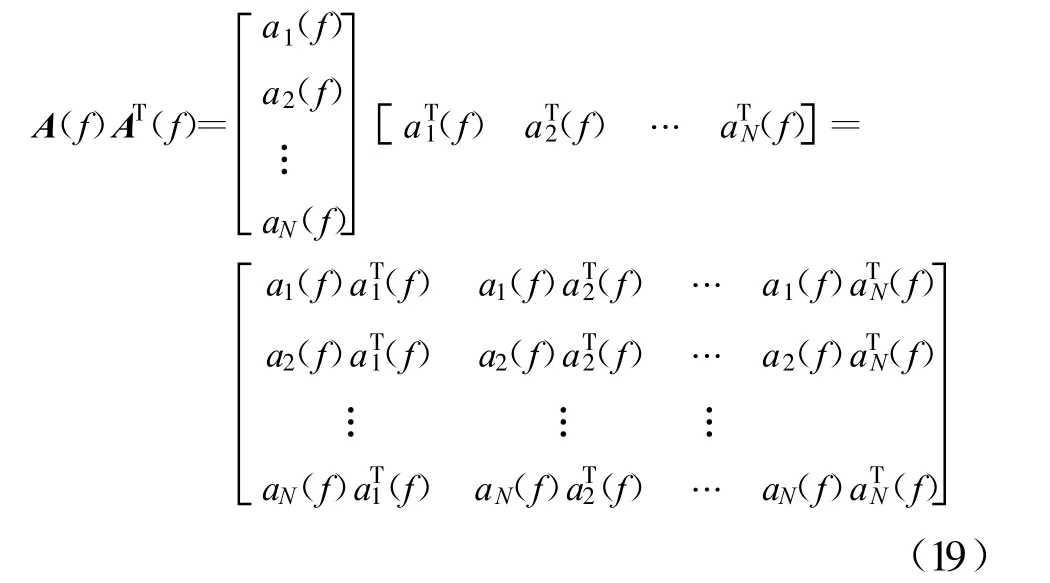

2.3 干扰温度与功率谱关联算法
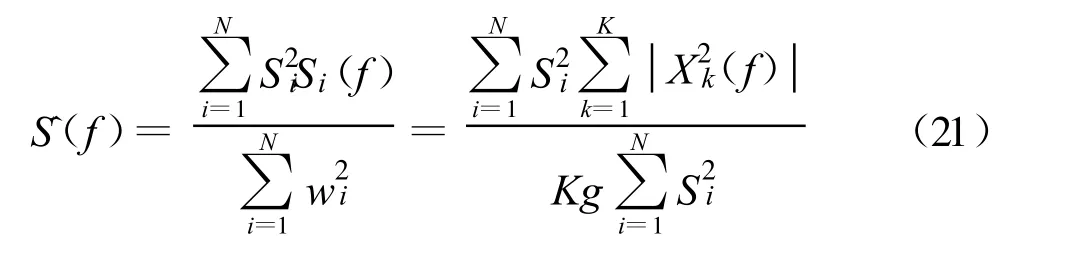

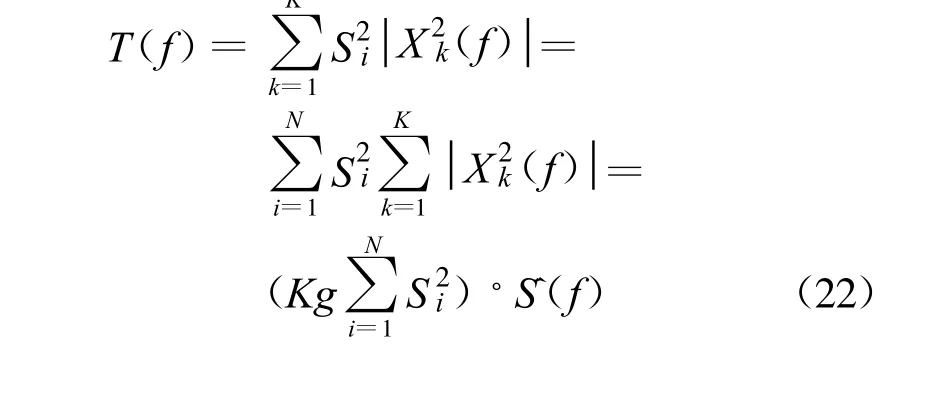
3 性能仿真


4 结束语

