分布式MIMO 中的最大似然频偏估计

邓 凯

(宜宾学院 物理与电子工程学院, 四川 宜宾644000)

1 引 言

众所周知,与单天线系统相比,多入多出(M IMO)技术可以在不需要额外的系统带宽的前提下显著提高数据传输的比特率[1]。而与采用集中式天线的传统M IMO 相比,采用分布式天线的分布式MIMO系统[2],由于各发射天线或各接收天线位于不同的地理位置,各收发天线对所对应的空间链路之间的相关性更小,因此能获得更高的系统容量[3]。

类似于单天线系统,在分布式M IMO 系统中同样会由于振荡器的不稳定性或者发射机与接收机之间的相对运动而产生载波频偏。频偏的存在会严重降低系统的信号检测性能[4],因此在检测之前必须进行准确的频偏估计和补偿。在分布式M IMO 中,由于各发射天线或各接收天线位于不同的地理位置,各收发天线对之间的频偏均可能不同[5],这使得其频偏估计问题变得更加复杂。文献[5-8]讨论了分布式MIMO 中的频偏估计问题,但是它们都缺乏对最具普遍意义的最大似然估计的研究,文献[5]虽然研究了信道与频偏的联合最大似然估计问题,但它需要求解一个n 维的最大化问题(其中n 是发射天线数),因此复杂度很高。

本文研究分布式MIMO 中的最大似然频偏估计问题。在考虑各收发天线对之间的频偏均可能不同的一般情况下,推导出了平坦衰落MIMO 信道模型下的最大似然频偏估计。针对收端是否采用分布式天线的两种不同情况,分别提出了一种频偏估计方法。所提频偏估计方法可以将一个n 维最大化问题分解为n 个一维最大化问题,从而大大降低计算复杂度,具有较强的实用性。

2 系统模型

考虑一个配置n 个发射天线和m 个接收天线的分布式MIMO 系统并假设MIMO 信道为平坦衰落信道。若频偏估计从t 0 时刻开始进行,则在频偏估计的过程中第k 个接收天线上的接收信号可表示为

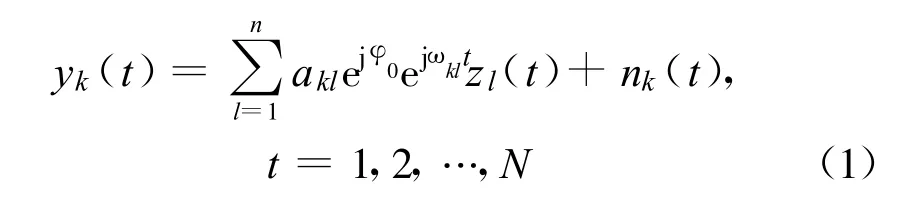
式中,zl(t)为已知的从第l 个发射天线发送的训练序列;N 为训练序列长度;akl和ωk l分别为第l 个发射天线和第k 个接收天线之间的信道增益和归一化(角)频偏,假设它们在训练序列持续时间内保持不变;φ0 为(-∞,t0)时间内由频偏累积的相位偏移,即频偏估计开始时的初相;nk(t)为第k 个接收天线上的零均值高斯白噪声序列。

通常,信道增益akl、频偏ωkl和初相φ0都是未知的参数。但在式(1)中,可以把初相并入信道增益的相位中,即定义akl(t 0)=akl ejφ0,而akl(t0)可由在t0时刻进行的信道估计获得。若假设信道估计是理想的,则akl(t0)就是一个已知的准确值。这样,接收信号里就只有频偏ωkl为未知参数,亦即待估计参数,因此式(1)可改写为

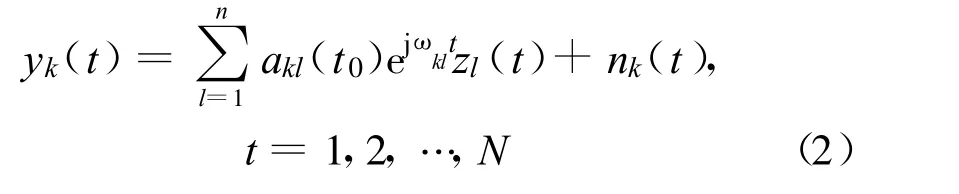
3 最大似然频偏估计

在实际的分布式MIMO 系统中,通常是基站处采用分布式天线,而移动台由于体积限制仍采用集中式天线。因此,对于下行链路来说,可以认为各发射天线与接收机之间的频偏均可能不同,而各接收天线与某一特定发射天线之间的频偏则都相同。这样,就可以利用所有接收天线上的接收信号进行联合估计,从而利用接收空间分集,进一步提高估计性能。

基于此,下面将分别讨论两种情况下的频偏估计:一种是考虑各天线对之间的频偏均不同的一般情况,这时只能各个接收天线分别进行独立估计;另一种即是考虑上述实际系统,这时可以利用所有接收天线进行联合估计。

3.1 独立估计

定义以下向量和矩阵:

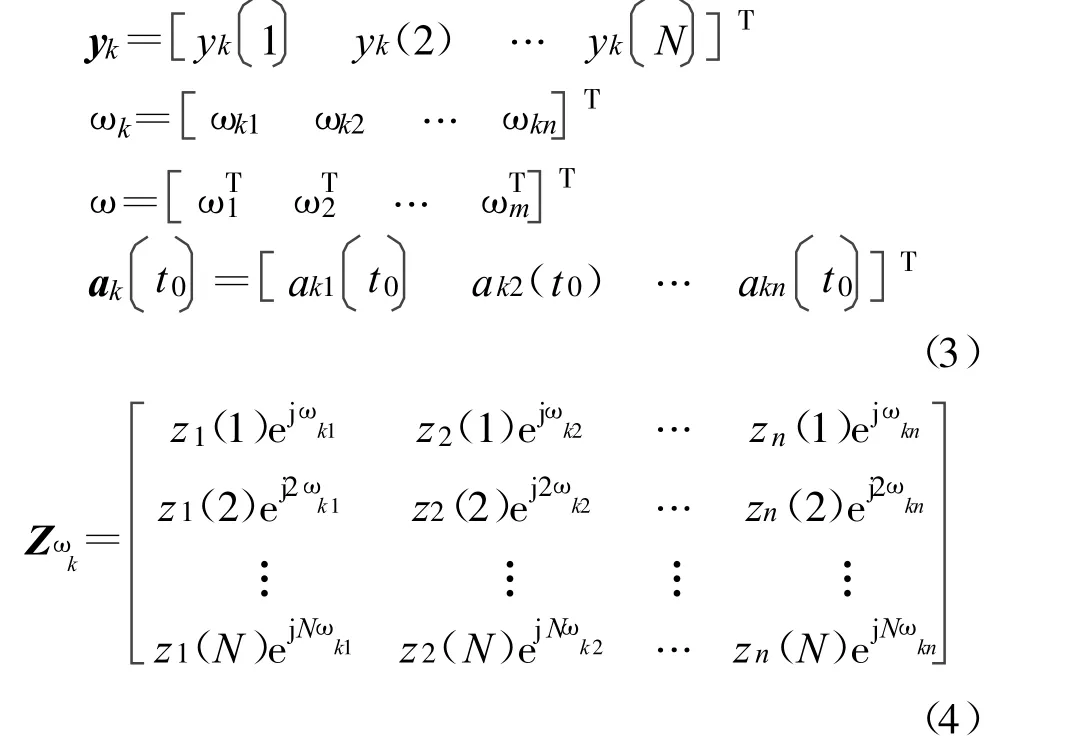
则通过式(2)进行最大似然频偏估计的负对数似然函数可以表示为

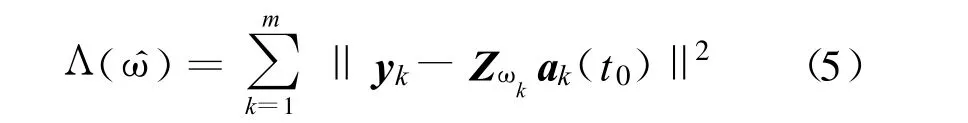
从上式可以看出,各个接收天线上的频偏估计可以独立进行。第k 个接收天线上的似然函数为

最小化此似然函数,即可得到第k 个接收天线上的频偏估计值:

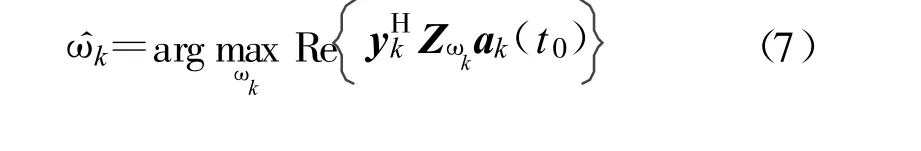
显然,该n 维最大化问题可分解为n 个一维最大化问题:

3.2 联合估计

若考虑实际系统中各接收天线与某一特定发射天线之间的频偏都相同这一情况,则可以利用所有接收天线上的接收信号进行联合估计以提高估计性能,此时第k 个接收天线上的接收信号为

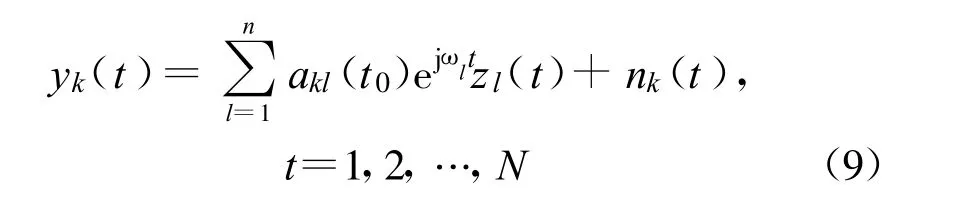
式中, ωl为收端与第l 个发射天线之间的频偏。

这种情况下的负对数似然函数为

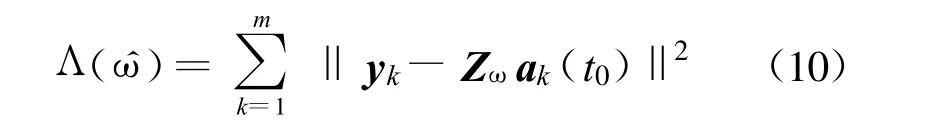
其中, ω=[ ω1ω2… ωl]T。则频偏估计值为

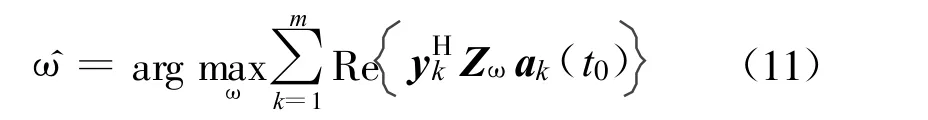
以上n 维最大化问题同样可以分解为n 个一维最大化问题:

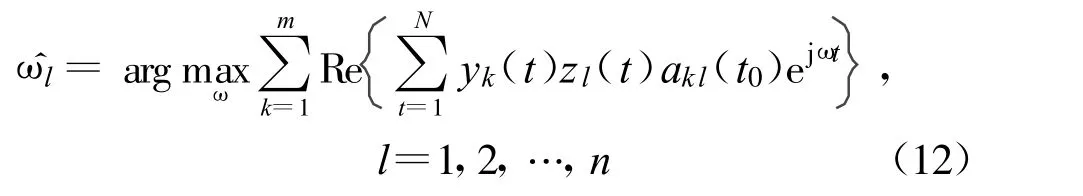
3.3 复杂度分析

由式(8)和式(12)可知,与文献[5] 所提方法需要求解一个n 维最大化问题相比,本文所提最大似然频偏估计方法仅需独立求解n 个一维最大化问题,从而大大降低了计算复杂度,具有较强的实用性。另一方面,联合估计由于利用了所有接收天线进行估计,因此比独立估计具有更高的复杂度,且随接收天线数呈线性增长。

4 仿真与分析

下面通过计算机仿真考察频偏估计的均方误差(MSE),分别给出以上提出的两种最大似然频偏估计方法在平坦衰落M IMO 信道下的估计性能。主要仿真参数如下:n =2, m =2, N =16, ω1=2π 0.1 0.105T,训练序列为随机产生的正交相移键控(QPSK)符号。在各接收天线独立估计的情况下只给出了第一个接收天线的仿真结果,而第二个接收天线有类似的结果。

两种频偏估计方法对第1 个发射天线(TX1)和第2 个发射天线(TX2)对应频偏的估计性能分别如图1(a)和(b)所示。

图1 频偏估计性能Fig.1 Performance of frequency offset estimation

从图中我们可以得出以下结论:

(1)两种估计方法在平坦衰落MIMO 信道下均可获得令人满意的估计性能,但在低信噪比(SNR)时会出现性能门限;

(2)各接收天线联合估计能够获得比独立估计更好的性能,这是由于联合估计利用了接收空间分集;

(3)实际应用中,由于信道估计误差的影响,所得到的实际频偏估计性能会比以上仿真结果稍差。

5 结 论

本文研究了分布式MIMO 中的最大似然频偏估计问题。与已有方法相比,本文所提最大似然频偏估计方法仅需求解一维最大化问题,因而具有较低的复杂度和较强的实用价值。仿真结果表明,所提方法在平坦衰落M IMO 信道下可以获得令人满意的估计性能;而在收端仍采用集中式天线这一特殊情况下,利用所有接收天线上的接收信号进行联合估计,可以进一步提高估计性能。

[1] Foschini G J.Layered space-time architecture for wireless communication in a fading environment when using multi-element antennas[ J] .Bell Labs Technical Journal,1996,1(2):41-59.

[ 2] Zhou S,Zhao M,Xu X,et al.Distributed wireless communication systems:a new architecture for future public wireless access[ J] .IEEE Communications Magazine,2003,41(3):108-113.

[ 3] Clark M V,Willis T M,Greenstein L J,et al.Distributed versus centralized antenna arrays in broadband wireless networks[ C]// Proceedings of 2011 IEEE VTS 53rd Vehicular Technology Conference-Spring.Rhodes:IEEE, 2001:33-37.

[ 4] Proakis J G.Digital communications[M] .4th ed.New York:McGraw Hill,2001.

[ 5] Besson O, Stoica P.On parameter estimation of MIMO flatfading channels with frequency offsets[ J] .IEEE Transactions on Signal Processing,2003,51(3):602-613.

[ 6] Pham T H,Nallanathan A, Liang Y C.Joint channel and frequency offset estimation in distributed MIMO flat-fading channels[ J] .IEEE Transactions on Wireless Communications,2008,7(2):648-656.

[7] Ma Huizhu,Liu Hui.Mu ltiple carrier frequency offsets estimation and compensation for distributed MIMO-OFDM systems[C]// Proceedings of 2012 2nd International Conference on Information Science and Engineering.Hangzhou:IEEE, 2010:4598-4601.

[8] Wang Hung-Chin,Wang Chin-Liang.A compact preamb le design for synchronization in distributed MIMO OFDM systems[C]// Proceedings of 2011 IEEE Vehicular Technology Conference-Fall.San Francisco, CA:IEEE,2011:1-4.