轨道交通移动闭塞安全距离的仿真研究

龙安宝

（中铁第四勘察设计院集团有限公司，430063，武汉∥高级工程师）

轨道交通信号系统中，相对于固定闭塞和准移动闭塞，移动闭塞是一种新型的闭塞制式。它不依赖轨道电路［1］，是以前车尾部为动态的极限目标点来决定列车追踪速度及距离的一种列车控制方式。在综合考虑信号系统性能指标、线路参数和列车性能参数等可能存在的最不利因素，并保证列车不越过极限目标点或不与前车发生冲突的前提下，列车的常规停车点与危险点（极限目标点）间的最小距离，即为该列车的安全距离。安全距离是为防止列车冒进信号而在防护点后方预留的一段距离，所以安全距离是移动闭塞系统中的关键。安全距离是综合考虑测速误差、不确定性位置等安全因素而具体设定的。本文将根据列车追踪间隔的计算原理，对安全距离的相关条件进行定性分析；同时结合移动闭塞的列车追踪间隔模型，对移动闭塞中安全距离进行仿真研究。

1 安全距离的概念

安全距离是基于列车安全制动模型计算得到的一个附加距离。它保证追踪列车在最不利条件下能够安全地停在前行列车的后方，不发生冲撞。所以，安全距离是移动闭塞系统中的关键，是整个系统设计的理论基础和安全依据。安全距离的基本概念［2］如图1所示。

图1 安全距离示意图

如图1所示，假定追踪列车在A点以线路允许的最高速度运行，此时前行列车处于C点。正常情况下，追踪列车开始进行常用制动，沿常用制动曲线，停止在B点。但是如果此时追踪列车发生故障，没有开始制动，反而以最大加速度加速，直至车载控制器检测到列车速度超出了容许范围（如曲线EF）；此后，车载控制器启动列车紧急制动系统，在紧急制动生效前，列车又沿曲线FG运行一段距离，然后制动力生效，列车沿紧急制动曲线紧急制动，停止在C点。考虑到列车的定位误差、速度测量误差等不确定性因素，列车停止的实际位置也有可能是D点。因此，将BD这段距离称作安全距离。

安全距离是附加在列车常用制动距离上的一段安全富余量。列车在行驶过程中，追踪列车和前行列车始终保持一个常用制动距离再加上一个安全距离的移动闭塞间隔，以确保在最不利条件下追踪列车和前行列车不发生碰撞。

2 安全距离的影响因素

国际上通用的移动闭塞中的列车安全距离是根据车载ATP（列车自动防护）的安全制动模型进行计算的［3］。该安全制动模型是考虑了线路、信号、车辆等各种安全相关的因素，是对安全距离进行计算的依据。

安全距离制动曲线如图2所示。其中，常用制动的特点是作用比较缓和，制动过程也较长，多数情况下，只使用50%的制动力［4］；紧急制动的特点是全列车的制动能力全部得到实施，反应在列车上制动比较迅猛，以致可能造成列车上的冲撞。影响安全距离的6个主要因素如下。

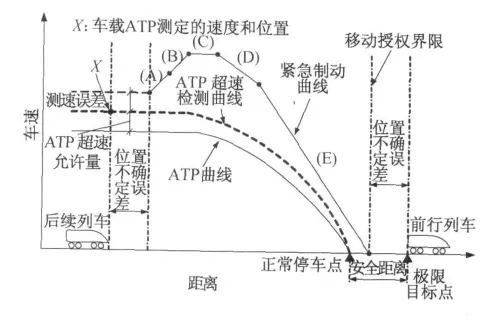
图2 安全距离制动曲线示意图

1）测速设备的误差：由于信号系统设备延时、测速设备精度、列车轮径磨损程度等不确定因素，均会造成列车测速和位置测量的误差。

2）信号车载设备响应过程：当信号车载设备测量到的列车速度和位置超出紧急制动触发曲线时，信号系统将向列车制动系统发出紧急制动指令。考虑到司机人工驾驶列车存在误操作的可能性，以及信号车载设备延时，按最不利情况考虑了列车加速运行阶段（A）。

3）列车的紧急制动过程：紧急制动过程包括列车牵引切断阶段（B）、列车惰性阶段（C）、列车制动力建立阶段（D）、列车制动力完全建立阶段（E）。该过程中各阶段的时间取决于列车特性参数，如列车制动系数、紧急制动激活时间、列车的滑动摩擦系数及不可预测的制动子系统故障等。在模型计算中的各参数取值将按照最不利情况考虑。

4）列车的位置不确定性：除考虑上述的测速设备误差、设备响应延时等因素外，还应考虑列车与轨旁设备间的响应时间、传输延时（包括允许的车－地通信中断时间）、列车最大允许退行距离等因素，从而在安全距离中考虑前车尾端和后车前端的位置不确定性。

5）轨道坡度：实际安全制动数学模型中，在（A）、（B）、（C）、（D）、（E）阶段还应将线路坡度相应产生的列车加速度考虑进去，从上述（A）～（E）过程可以看出，有利于列车加速而不利于列车制动的因素均会增大安全距离。

6）追踪列车制动前的运行速度vmax：vmax越大，列车需要的制动力越大，制动距离越大，因此对应的安全距离越长。

3 安全距离对列车追踪间隔的影响

安全距离是附加在列车常用制动距离上的一段安全富余量，因此安全距离是列车追踪间隔时间的一个重要组成部分。城市轨道交通以“小编组，高密度”为发展目标，因此如何缩短行车间隔是首先需要研究的问题。现结合移动闭塞列车追踪间隔模型，仿真分析在车站的安全距离对列车追踪间隔时间的影响。

3.1 列车的追踪间隔模型

在移动闭塞条件下，前后两列车在车站的最小安全间隔是指：前行列车刚刚出清车站，且驶过安全保护区段LS，后续列车以区间最大允许速度vmax行驶，并且距车站入口的距离正好等于列车制动距离加上制动反应时间内列车驶过的距离，如图3所示。

图3 移动闭塞条件下两列车在车站的最小安全间隔

为了方便分析问题，先提出一些与实际情况差别不大的假设：前后两列车具有相同的起动加速度a、制动减速度b、列车长度LT、安全保护区段LS，列车最大允许速度vmax。

1）前行列车出清车站并驶过安全防护区段LS的时间为t1。t1的计算又分为两种情况：

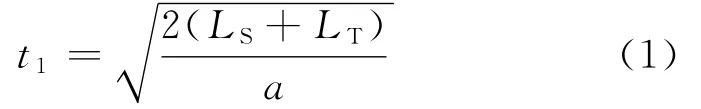
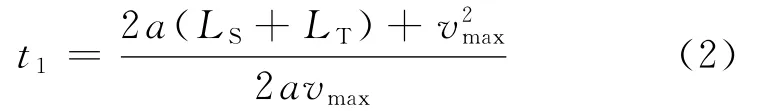
2）后续列车以vmax行驶时的制动反应时间tR，包括列车司机、列车设备的反应时间。

3）后续列车以vmax开始制动到停稳的时间tB，其值为vmax／b；

4）后续列车在车站的停车时间tD。

故列车安全间隔时间tZ可分为t1、tR、tB、tD四部分，即tZ＝t1＋tR＋tB＋tD。

由此可得到移动闭塞的tZ计算公式为：

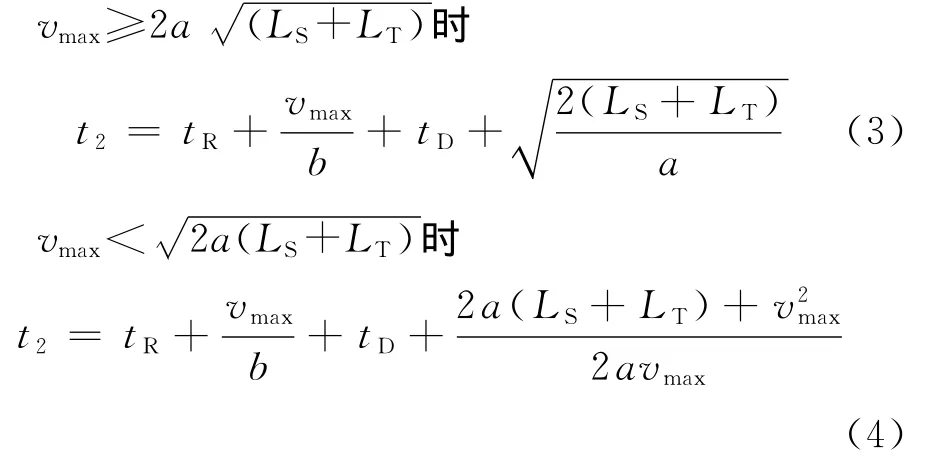
3.2 仿真计算与结果分析

城市轨道交通车辆分为A、B、C三种型号，其具体参数见表1所示。A型车的尺寸最大，运能最高。

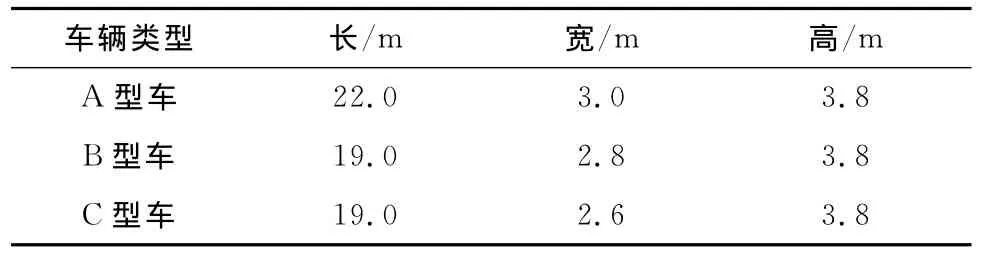
表1 城市轨道交通不同型号车辆的基本参数

从列车间隔时间仿真的角度来看，B型车和C型车具有相同的车长，仅宽度不同，所以B型车和C型车可按同一类车考虑。本文的仿真以城市轨道交通为背景，并按照B型车4节车编组计算列车的总长度。计算车长时纳入了各节车连挂的长度。设定的参数如下：

1）B型车列车长度LE＝80m；

2）起动加速度a＝0.9m／s2，

3）制动减速度b＝1m／s2；

4）制动反应时间tR＝1s；

5）列车允许最高速度vmax＝120km／h；

6）后续列车在车站的停车时间tD＝30s。

按上述设定参数值，由式（3）可得图4、图5，由图4可得表2。

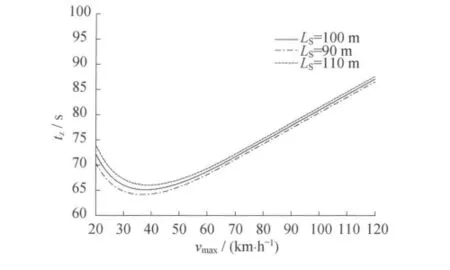
图4 不同LS下，vmax与tZ的关系

图5 不同vmax下，LS与tZ的关系

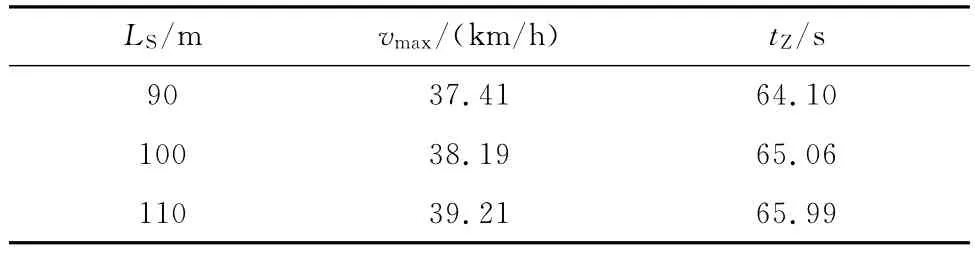
表2 不同LS下vmax与tZ的优化值

根据上述的仿真计算，可得如下结果：

1）vmax和LS是影响列车追踪间隔的主要因素。

2）当vmax一定时，tZ随LS的增大而增大，且基本呈线性关系。

3）当LS一定时，tZ与vmax的关系曲线类似于抛物线。由表2可得，vmax越小，LS越小，且能保证较小的列车追踪间隔时间。

4）在不同的vmax下，tZ都随着LS的增大而增大。在vmax相对较小时，随着LS的增大，tZ变化显著；在vmax相对较大时，随着LS的增大，tZ变化趋于平缓。

5）从图4、图5可看出，移动闭塞基本能保证列车间最小追踪间隔在90s以下。

4 结语

在移动闭塞条件下，tZ、vmax、LS之间存在一定的规律。通过对vmax和LS的调整，可以进一步缩短列车追踪间隔时间，并能够满足tZ小于90s的要求，达到了现有运营的需求。

［1］谢肇桐.移动闭塞系统［J］.铁道通信信号，1996，2（32）：35.

［2］陈锋华.浅谈移动闭塞的基本原理［J］.铁道通信信号，2005，41（2）：12.

［3］IEEE Std 1474.1TM－2004.IEEE Standard for Communications-Based Train Control（CBTC）Performance and Functional Requirements［S］.

［4］刘晓娟，张雁鹏，汤自安.城市轨道交通智能控制系统［M］.北京：中国铁道出版社，2008.

［5］张济民，吴汶麒，张树京.准移动闭塞列车安全间隔时间的计算［J］.铁道学报，1999，21（3）：6.

［6］罗雁云，吴汶麒.城市轨道交通移动闭塞列车安全间隔时间分析［J］.中国铁道科学，2005，26（1）：119.

［7］金娟，杨梅，王长林.基于移动闭塞原理的地铁列车线路通过能力的研究［J］.铁路计算机应用，2008，17（6）：7.

［8］徐启禄.运行干扰条件下的列车追踪运行仿真［J］.城市轨道交通研究，2011（11）：72.