论地下水超采与地面沉降
薛禹群
(南京大学地球科学与工程学院,江苏南京210093)
1 造成地面沉降的主要因素
地面沉降是一种可由多种因素引起的地面高程缓慢降低的环境地质现象,严重时会成为一种地质灾害。造成地面沉降的原因很多,有天然因素,也有人为因素。天然因素中主要有:新构造活动、海平面上升以及地壳构造活动等。欠固结土层的自然压密也应属于这一类。人为因素中主要的有:过量开采地下水以及石油、天然气开采、地热利用等。近年来随着城市高层建筑的增多,由此造成的沉降也日益明显。人类活动和地质作用是造成地面沉降的主要原因,其中过量抽取地下水是最主要的原因。我国和世界上主要的地面沉降区都是由过量开采地下水造成的。出现地面沉降的地区一般范围大,沉降过程缓慢,所以早期一般不易察觉,也不易引起人们的重视。它多发生在大中城市,对人们的生产、生活、交通等影响极大,造成的损失和危害也大,成为一种严重的环境地质问题,影响和制约着当地国民经济的可持续发展。所以2002年10月1日时任副总理的温家宝曾批示“超采地下水造成地面沉降在许多地方呈加剧趋势,已给经济建设和人民生活带来大的损失和危害,并成为影响生态环境和可持续发展的一个重大问题,必须引起足够重视并采取综合措施加以解决”。
既然过量抽取地下水是造成地面沉降最主要的原因,哪为什么要过量开采呢?这不能不从我国水资源的特点说起。人类的生产、生活离不开水。水资源是关系国家经济安全的重要战略资源,也是经济和社会可持续发展的重要保证。我国水资源总量不算少,28124×108m3居世界第六,但人均占有量低,不足2 200 m3,在全球大致排128位,不到世界人均数的1/3。地下水是水资源的重要组成部分,在保障城乡居民生活、支持经济社会发展和维护生态平衡等方面具有十分重要的作用,尤其是在地表水资源短缺的北方地区(资源性缺水)和南方局部地区(水质型缺水),地下水具有不可替代的作用。经济的快速发展,人们对水的需求日益增加,因而我国地下水的开采量一直呈明显增长态势,从20世纪70年代的约572×108m3,增加到80年代的748×108m3,1999年达到1 116×108m3。地下水供水量的比重也从80年代初的14%,上升到目前的近20%。由于缺乏有效管理、无节制的长期集中过量开采地下水,开采量远大于补给量,造成地下水水位持续下降,局部地区出现含水层疏干现象。华北平原长期严重超采,山西六大盆地、关中平原、松嫩平原、下辽河平原、西北内陆盆地的部分流域(石羊河、吐鲁番盆地等)、长江三角洲、东南沿海平原等地区整体或局部超采也十分突出。据不完全统计,目前已形成大型地下水降落漏斗100多个,面积达15×104km2,超采区面积62×104km2,造成众多泉水断流,部分水源地枯竭。著名的大漏斗有河南的安阳-鹤壁-濮阳漏斗、山东的淄博-潍坊和莘县-夏津漏斗,漏斗面积依次超过 6 000、5 000、4 000 km2。
2 我国的地面沉降
大量开采地下水,导致形成大面积的地下水位降落漏斗。地下水水头的降低,改变了开采含水层及其上、下弱透水层的应力状态,不仅开采含水层释水,弱透水层也释水,从而引起土层压缩,导致地面沉降变形,出现地裂缝。由于长期过量开采地下水,导致由此诱发的地面沉降不断加重。据有关部门不完全统计,截止到2000年,全国地面沉降区的面积超过10×104km2。华北平原和长江三角洲是其中两大著名的区域地面沉降带,此外汾(河)渭(河)河谷、松嫩平原、下辽河平原、东南沿海平原的一些城市也产生了较严重的地面沉降灾害。上海、天津、西安、太原、沧州等市沉降中心的累计沉降量均已超过2 m,有的已超过3 m,如天津塘沽。我国的这些地面沉降总体上可以分为两种类型:①主要由过量抽取地下水引起的,长江三角洲的地面沉降就属于这种类型;②在构造沉降的基础上,由开采地下水、油气、地下热水等形成的地面沉降,天津和河北平原就属于这种类型。地面沉降导致建筑物基础下沉、房屋倒塌、路基裂缝、管线开裂、严重影响建筑物的正常使用和寿命,影响地铁、越江隧道、桥梁、高速公路、高速铁路、城市供水、供气等地下管网、高层建筑等的正常营运;损失地面高程,使洪涝灾害加剧,防洪、排涝工程效能下降,雨季积水难排;桥下净空减小,内河通航能力下降。除直接经济损失外,间接经济损失更大。由于不均匀沉降,一些地区还产生了严重的地裂缝灾害。陕西、山西、河北、河南、山东、江苏、安徽等省较为发育。目前全国1 000余处、6 000多条。
地面沉降是一种世界性的地质灾害,世界上有200多个城市或地区发生不同程度的地面沉降,最大地面沉降已接近或超过10 m,如墨西哥从城、美国的San Joaquin峡谷。
3 土层变形的特点
地面沉降量与该地各个土层的变形特点有关,可以通过分层标附近观测孔中该土层水位和分层标测得的该土层变形量的关系曲线来表达。它大致和土力学中的应力-应变曲线相当。长江三角洲地区大量的分层标和水位观测资料证实不同的土层(包括含水层、弱透水层)表现出不同的变形特点,有:弹性变形、弹塑性变形、粘弹性变形和粘弹塑性变形等多种变形。土层变形量不仅与土层性质有关,还与土层所经历的地下水位变化情况有关。土层中地下水位的变化实质上反映了土层所经历的有效应力的变化过程,因此会影响土层的变形。由此不难看出,由于土性和土层所经历的地下水位变化模式的不同,区域地面沉降中土层的变形特征会表现出明显的地区差异性。不仅不同的土层会表现出不同的变形特征,同一土层在不同地区由于处于地下水位降落漏斗的不同部位,水位变化模式不同也会有不同的变形特征。在降落漏斗的边缘部位土层常表现为弹性变形,如图1a所示,上海第四弱透水层位于降落漏斗边缘的点只有很小的残余变形量,以弹性变形为主。但在漏斗中心部位则为粘弹塑性变形,而在两者间可能还有过渡类型,只是由于没有足够的分层标观测资料,无法加以进一步论证。更为重要的是同一地点的同一层土,在不同的沉降阶段,由于水位变化模式不同而表现出不同的变形特征。上海漏斗中心部位上棉十七厂分层标1991年前后第四承压含水层的变形分别表现为弹性变形和粘弹塑性变形就是明证。常州清凉小学分层标也显示出类似特征。前述第四弱透水层以杂色黏土、粉质黏土为主,也有类似的特征,它位于降落漏斗中心附近的分层标显示在1991年以前,以弹性变形为主。1991-1993年地下水位周期升降过程中存在明显的残余塑性变形;1993年以后,水位上升时已基本上看不到回弹变形,代之以持续的压缩,变形明显滞后(图1b)。另一点需要强调的是含水砂层的变形并不是前人所认为的“弹性变形”,上海、常州长期分层标观测资料、室内试验都证实上海的第四、第五承压含水砂层(图2)和常州的第一、第二、第三承压含水砂层不仅变形是非线性的,而且都存在变形滞后(图3)。这种滞后主要与蠕变有关,因此和认为含水层中的砂土变形与应力变化同时完成的观点不同,砂土也有蠕变变形,只是蠕变变形量要比黏土的小,我们为此进行的室内试验也证实了这点(图4)。
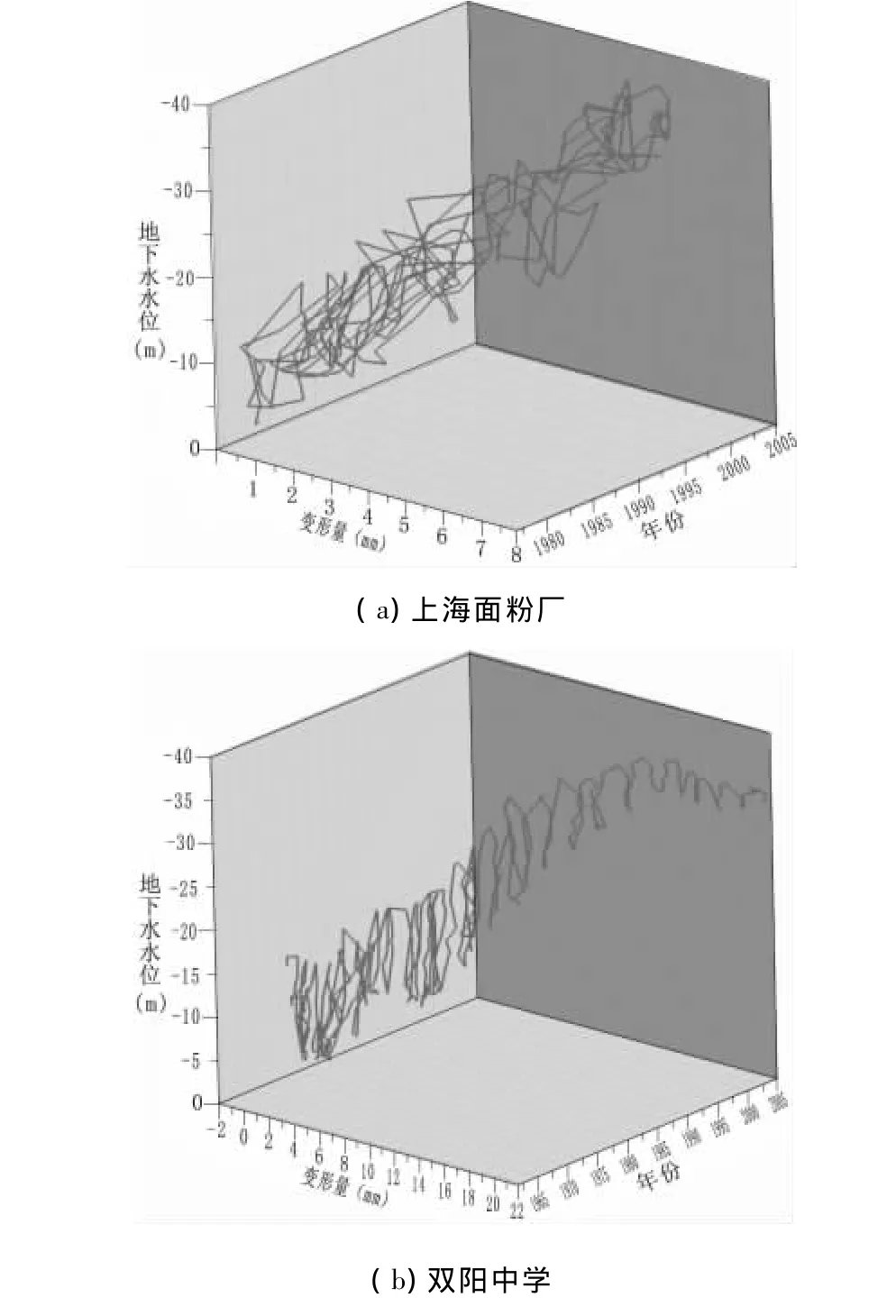
图1 上海第四弱透水层水位-变形量-时间曲线

图2 上海第四承压含水层水位-变形量-时间曲线(上棉17厂标 )
4 地面沉降的防控与地面沉降模拟
地面沉降造成巨大损失,因此各国科学家也在不断研究防控地面沉降的办法。虽然方案、办法很多,由于地面沉降是由过量开采地下水引起的,所以最根本、最有效的办法还是严格控制地下水开采。如何控制地下水开采量?目前得到各国科学家广泛认可的科学方案是通过建立区域地面沉降模型来预测不同地下水开采方案和开采量所可能带来的沉降量,进而根据优化原理确定最佳开采量和最佳开采方案。也就是说控制地面沉降的主要措施在于加强地下水资源的管理,优化地下水开采布局,控制地下水开采量和开采层次,科学合理地开发利用地下水资源。此外,开展地下水人工回灌,增加补给量以控制地下水位下降也是有效的,但有清洁的回灌水源是必要条件。调整开采层次作为一种辅助措施,在一定阶段有助于控制地面沉降,但不能从根本上解决问题。上海早期主要开采第二、第三承压含水层,,以后采取压缩开采量、增加人工回灌量、逐步调整开采层次,取得了较好效果。如果地下水开采量不减少,则随着开采层次的调整,新的主采层的沉降量会逐步增加,甚至成为形成沉降变形的主要层位。分析1986—1998年的上海实际观测资料不难发现,1986-1991年期间,第二承压含水层以上的浅部土层在总变形量中所占的比重较大,沉降主要发生在浅部土层中。1992―1998年,浅部土层变形所占的比例减小,相应的深部土层会随着开采量的增大(一度第四、第五承压含水层的开采量已分别占全市开采量的70%和15%左右),使第四承压含水层的变形在总变形量中所占的比重大幅提高,平均达49.27%,部分地区还要大,如标3分层标的观测资料证实,第四承压含水层的变形量1986-1991仅占地面总沉降量的18.8%,而1992-1998期间迅速增至70.9%。相反,第二、第三承压含水层1995年前所占的比重只有4.87%。
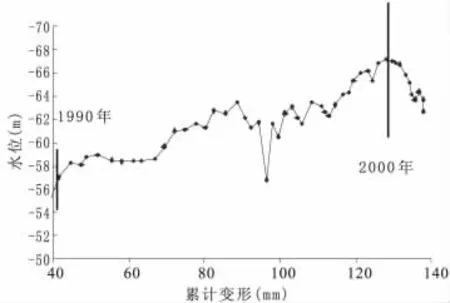
图3 常州第三承压含水层水位-沉降量曲线(清凉小学分层标)

图4 常州饱和砂性土在不同压力下的蠕变曲线
综上所述,控制地面沉降的主要措施在于加强地下水资源的管理,优化地下水开采布局,科学合理地开发利用地下水资源。要做好这项工作关键在于要建立一个能切实反映该地区实际情况的区域地面沉降模型来预测不同地下水开采方案和开采量所可能带来的沉降量,进而根据优化原理确定最佳开采量。为此除了要掌握好必要的水文地质知识、数值模拟理论和技能外,还必须掌握该地区所有土层变形特征、熟悉它们的应力-应变关系(常用水位-变形量曲线来代替),据此才能建立反映这些特征的不同的沉降模型。对于一个大区域来讲,土层变形特征是多种多样的,很可能土力学中的各种模型在你那儿都会出现,因此必须有多种沉降模型与之匹配,企图用一种模型到处套用是万万不行的。虽然土力学中已经建立了各种各样的理论模型,但在地面沉降中往往难以应用,主要原因在于所含参数太多,在实践中难以测定它们的值。因此往往需要另行寻找适合的模型。在进行长江三角洲地面沉降模拟中,变形虽然复杂,各地区各时段差别很大,但就其类型来说却是有限的,如前述,大致可归纳为4种类型,即弹性变形、弹塑性变形、粘弹性变形和黏弹塑性变形。当然不同土层、不同地区、不同时段,具体采用的模型和模型中的参数是各不相同的。这4种模型中,前3种前人做过不少工作,但最后一种在地面沉降中研究甚少。虽然土力学中也有不少理论研究,但用到具体地面沉降中还有不少困难,难以应用。为此必须建立一种理论上比较严密,涉及的参数少的模型,以便在大区域实际地面沉降模拟中应用。循此思路,我们通过改造Merchant模型做到了。即把两个虎克弹簧体a、b改成能反映弹塑性变形的非线性弹簧体,当土体有效应力小于先期固结压力,弹簧体a、b的变形都是弹性的,此时弹簧体a和由b和组成的开尔文体可以刻画瞬时弹性把原先只能描述黏弹性应力-应变关系,无法刻画当土体有效应力大于先期固结压力后,土体发生的黏塑性变形的Merchant模型(图5),改造成能够刻画瞬时弹性、瞬时塑性变形以及黏弹性、黏塑性变形的模型,满足了模拟要求。而且涉及的参数少,适合大区域地面沉降模拟。我们称它为修正的Merchant模型。它刻画黏弹塑性变形的沉降方程为
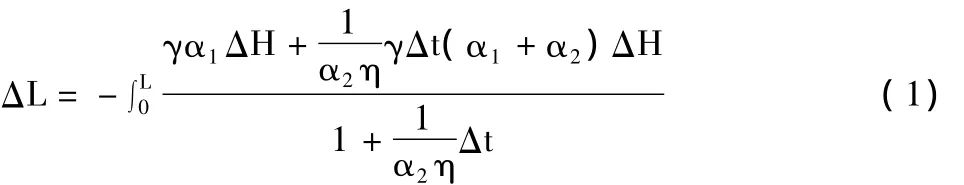
式中:为土层垂向变形(沉降)量;α1,α2分别为模型中两个弹簧的体积压缩系数;η为模型中牛顿黏壶的黏滞系数;γ为水的容重;ΔH=H-H0,H为t时刻的水头,H0为每一时段的初始水头;L为土层厚度。参数取值如下:

式中:αke1和αkv1分别为Merchant模型中弹簧 a的弹性和塑性体积压缩系数;αke2和αkv2分别为弹簧b的弹性和塑性体积压缩系数;HP为土层历史上曾达到的最低水头。通过对(1)式的简化,即通过改变参数可以得到弹性、弹塑性、黏弹性变形条件下的沉降模型。如令η=∞,α1=α则有弹性变形条件下的模型

如将(1)式中的 α1,α2都取为常数,即 α1= αke1,α2=αke2,便得黏弹性变形条件下的沉降模型,它与(1)式在形式上相似。弹塑性本构关系下的沉降模型和弹性本构关系条件下的沉降模型(3)类似,只是体积压缩系数在弹性变形和塑性变形条件下取不同的值,即η=∞,

由此不难看出,我们修正的Merchant模型包括了弹性、弹塑性、黏弹性、粘弹塑性模型,前三种模型只是修正Merchant模型的特例。通过改变模型中的参数设置就可以得到前面三种前人导出的沉降模型。这样就大大简化了复杂条件下大区域地面沉降模型的建立,一个一、两万平方千米甚至更大达数万平方千米的区域可以放置在一个模型中,通过改变参数设置来建立内部各个小区域的沉降模型,运算起来异常方便。
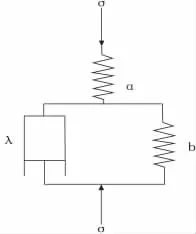
图5 Merchant模型
除了沉降模型外,还要配以相应的水流模型。需要注意的是通常看到的水流模型(如《地下水动力学》中的模型)都是以弹性变形为基础的,在地面沉降模拟中必须作相应的修改,使它和与它耦合的沉降模型的本构关系一致起来。即黏弹塑性沉降模型与相应的黏弹塑性条件下的水流模型耦合,弹性沉降模型与相应的弹性条件下的水流模型耦合等。黏弹塑性本构关系下的水流方程为
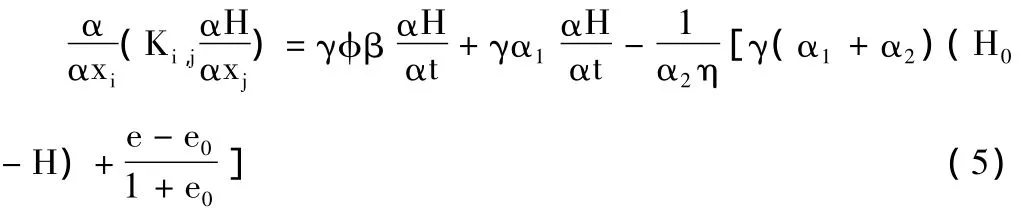
式中:e为孔隙比;e0为初始孔隙比。弹性变形条件下的水流方程为

式中:α为土的体积压缩系数。弹性变形条件下,土层中的水流方程与(5)式相似,只是其中的体积压缩系数α1、α2是常数。余类推。
在沉降过程中,土层压缩,渗透系数、贮水系数等水文地质参数也会随之改变。因此与之配套的水流模型不能像传统的水流模型那样是常系数的,应该是变系数的,随着不断沉降改变这些参数值。所以水流模型和沉降模型应该很好地耦合,以反映可能长达几十年的过程中压缩沉降对水文地质参数的影响。虽然目前做到完全耦合还有困难,但也不应像有的模型那样采用两步走的方案,名为耦合,实则各行其是,无法反映在沉降影响下,参数的不断变化。
最后还有一个问题也是需要解决的,即每层土垂向上的厚度少的往往只有几米,多的往往也不过几十米,而它们在水平方向的展布则有数千、甚至数万平方千米,如果按垂向尺度划分单元,则三维问题所需内存量很可能超出一般计算机的容量;如果加大水平方向单元的尺度又面临同一个单元水平和垂直方向尺度相差过大造成单元畸形的问题。为此我们引入了一种国际水文地质界甚少应用的新的算法——多尺度有限元法,这种方法通过基函数本身满足简化的渗流微分方程,不再要求单元内的参数是常数,即单元内的参数可以是非均质的,这时介质的非均质性已通过解渗流定解问题反映到基函数上面了。即一个单元内可以存在参数不同的介质,如含水层和弱透水层,所以能克服前面提到的内存大和单元畸形问题。后来又以密集精细剖分的Galerkin有限元法再次计算同一上海地区,两种方法的结果比较接近,证实多尺度有限元法不仅能克服前述困难,且能以较少的单元得到比较满意的结果,远较传统的一般有限元法的结果为好。
有了区域地面沉降模型作为基础,就可以预测不同开采方案和开采量所可能带来的沉降量,通过优化确定最佳开采量,科学合理地开发利用地下水资源,同时避免引起大规模的地面沉降。禁采地下水,作为一种严重沉降区的应急措施来恢复降落漏斗区内的地下水水位,控制地面沉降未赏不可,但作为一种长远措施就不合适了,因为水位恢复后依然禁采,这些优质的地下水就会流向大海,白白浪费了。有关这个问题已说过多次,这儿就不多说了。
有了区域地面沉降模型、有了优化的水资源管理模型、制订了周密、科学合理的开发利用规划,并不意味着地面沉降的监控任务可以顺利完成了。中间还有一个重要的环节有没有足够的监测资料来满足建模的需要?国内外往往由于缺乏必要的区域性地面沉降监测网,所以难以掌握地面沉降整体的变化规律,因而难以进行上述各项工作。为此国家已经决心建设“国家地下水监测工程”,“建成一个满足于国家需求的地下水监测网络”,由水利部和国土资源部有关部门负责执行,其中就包括有关地下水水位和地面沉降量的监测内容。希望早日通过各方面的“评价”,开工建设,早日建成,造福国家。
最后应指出,这项工作看起来似乎并不困难,具体做起来难度还是不小的,很多问题并没有现成的答案,需要通过刻苦研究才能解决。就拿建模来说吧,由于各地千差万别,必须逐层、逐地、逐时段研究它的变形类型,弄清楚它的本构关系,才能建立相应的沉降模型。一些年轻人中往往有一种错觉,似乎只要学会用MODFLOW等软件后就什么都解决了,于是把精力放在盲目追求所用软件的版本,过分追求模拟结果的可视化程度,而不重视对研究区具体水文地质条件的认识、概化,轻视土体变形特征的研究和概念模型的建立。MODFLOW等软件有它的优越性,使用方便,对解决生产实际中的一些问题非常有用,特别是它的前后处理很好。但它本身对一些问题的处理还存在不足是必须注意的。例如它的变形类型非常有限,仅一、二种而已,根本无法满足实际变形复杂、多样性的需要。在地面沉降中蠕变变形起着非常重要的作用,不仅黏性土可能发生蠕变。砂砾含水层也可能发生蠕变,长江三角洲大量分层标资料证实了这一点,室内试验也证实了这点。二十多年前江苏常州清凉小学打钻时,第三承压含水层砂样呈松散状,无法取样;但二十多年后在差不多同一地点打钻却可以取上完整的岩芯,长达近1米的岩心托在两手间完全不用担心会断裂。这种变形在长三角很多地方都可以见到,它是MODFLOW等软件少数几种变形模型无法描述的。不考虑这类变形也就无法正确描述长三角、天津等地出现的水位上升并恢复到差不多沉降前原先的位置,但沉降仍在继续的问题,即沉降滞后的问题,因而无从完整勾画出地面沉降的实质。此外,MODFLOW本身还存在不足,也是需要注意的。另外,MODFLOW用的是有限差分法,它自身也有些不足的地方,因此除了加密剖分,引起所需存贮量可能超出一般计算机容量外,难以像有限元法那样引用多尺度有限元法既克服单元畸形问题,又减少单元总数。因此,必须从基础研究开始,自己动手编写软件,才能有所创新。
5 结语
控制地面沉降的关键是控制地下水开采,做到量入为出,改变无节制的开采。只要做到这点,控制地面沉降是不难的。地面沉降既然是一种主要由人类活动引起的一种环境地质问题,相信人类在认识它的规律后,也会认真反思自己的行动,收敛自己的行为,从而朝着彻底根治这种危害人类的地质灾害不断前进。

