计及风速扰动的含风电场电力系统相关性分析研究

孙 琦，尤红丽，辛 鹏，王斯琦

(1.东北电力大学电气工程学院，吉林吉林132012;2.吉林省电力有限公司吉林供电公司，吉林吉林132012)

0 引言

随着风电所占比例增加，对系统稳定性的影响越来越大。波动性和季节性的新能源发电的风电［1-2］，在带来大量绿色可再生能源的同时，也可能将电网带入一个扰动更频繁、扰动量更大、非平稳性和随机性更强的环境中。在这样的环境中，如何合理的计及风电接入对系统的影响对电网安全运行具有重要意义。文献［3-5］提出了利用相关分析理论进行故障选相。文献［6］提出了基于相关分析的暂态差动保护原理。文献［7］将其应用到中长期电力负荷综合预测中。文献［8］对新能源发电功率与电压偏差进行了相关性分析。文献［9］在风电场随机潮流计算中计及了有功无功相关性。但是，目前，估计电力系统信息关联程度的分析方法仍然很少，特别是考虑风电接入系统后对系统关联程度及其影响的几乎未见涉及。因此，本文提出了一种快速估计风电接入系统系统相关程度的新方法。它采用相关分析法快速估计各发电机有功功率，并基于不同风速情况，对系统相关程度作出评价，综合分析风电接入对系统的影响。

1 永磁直驱风电机组的数学模型

永磁直驱风电机组(Permanent Magnet Synchronous Generators，PMSG)的基本结构如图1所示。

图1 PMSG风力发电机组示意图

1.1 风力机数学模型

风力机基本原理是利用风轮接收风能，将其转换为机械能，通过风轮轴输送出去。由空气动力学原理可知，风力机的输出功率Pm满足［10，11］:

式中:A为桨叶扫风面积;θ为桨距角;ρ为空气密度;λ为叶尖速比;Vw为风速;ωw为风力机转子转速;R为风力机转子半径;Cp为与θ和λ有关的功率系数。

风力机从风中捕获的功率满足:

则风力机的机械输出转矩Tw可表示为

风电机组轴系统模型为

式中:ωr为发电机转子转速;Bm为等效转动惯量; Te为电磁转矩;Jeq为转动粘滞系数。

1.2 PMSG数学模型

根据转子磁场定向得到同步旋转坐标系下的PMSG的定子电压方程为［12］

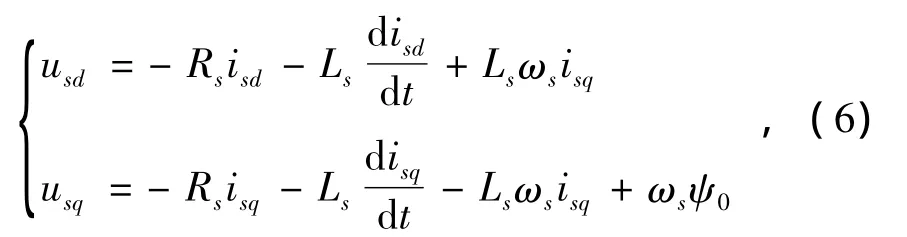
式中:isd、isq和usd、usq分别为永磁同步发电机定子输出电流、电压的d轴和q轴分量;Rs和Ls分别为发电机的定子电阻和电感;ωs为同步电角速度;ψ0为永磁体的磁链。

电磁转矩的表达式为

PMSG的永磁体多采用径向表面式分布，即Ld=Lq，此时发电机的电磁转矩可简化为

式中，np为发电机的极对数。

由于发电机的电磁转矩与定子q轴电流成正比，因此通过调节isq即可调节永磁同步发电机的电磁转矩，进而调节发电机和风力机的转速，使之随风速变化，运行于最佳叶尖速比状态。

2 相关性、相关分析和相关系数

相关性是指信号的相似和关联程度。相关分析不仅可用于确定信号，可用于简单而且对噪声有抑制能力的信号，所以相关分析在机械振动分析、微弱信号检测中有一定应用。相关性常用相关系数或相关函数来描述［13］。

对于随机信号而言，变量x和y之间的相关程度可以用相关系数cxy表示，即

式中:n为离散点编号;N为离散点总数;rxy为变量x、y的协方差;rx、ry为变量x、y的标准差;μx、μy为变量x、y的数学期望(x、y为离散随机信号时)或均值(x、y为连续信号时)，即

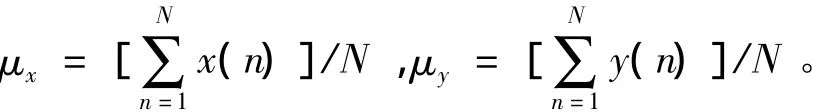
在信号处理中，有时会将μx、μy从式(9)中略去。当x、y为同一信号时，一般称自相关系数，不称为互相关系数。

本文相关系数使用说明如下:

1)相关系数没有单位，其值为-1≤cxy≤1。cxy值为1或接近1表示正相关，可判为同相，即两功率信号同调;cxy值为-1或接近-1表示负相关，可判为反相，即两功率信号相互振荡;cxy值为0或接近0表示不相关。

2)cxy绝对值反映两变量间相关关系的密切程度，绝对值越大说明相关性越强，cxy绝对值等于1为完全相关，cxy=0为零相关。

3 风速模型

由于风力发电机组的输出功率随着风速变化而变化，因此，电网将持续受到风电场功率扰动源的干扰。风速的持续变化在一定时间和空间范围内是随机的，但从总的、长期统计结果来看，风速的变化仍然具有一定规律。风速变化原则上可由基本风、渐变风、阵风、随机风组成［14-15］。

3.1 基本风

基本风在风力机正常运行中一直存在，它决定了风力发电机向系统输送额定功率的大小，反映了风电场平均风速的变化。它可以由风电场测风所得的威布尔(Weibull)分布参数近似确定:

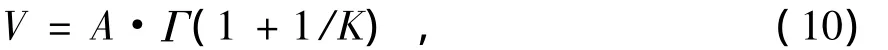
3.2 阵风

式中，VWG、T1G、TG、maxG为阵风风速、启动时间、周期和最大值。

3.3 渐变风

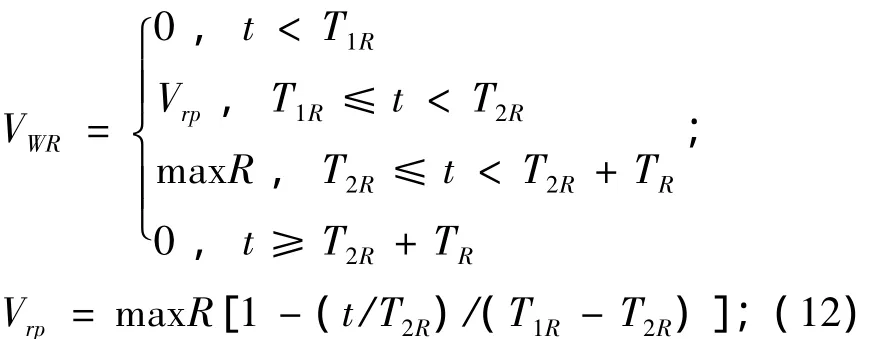
式中:VWR为渐变风速，m/s;maxR为最大值，m/s; TR为保持时间，s;T1R为起始时间，s;T2R为终止时间，s。

3.4 随机风

式中:φi为0～2π之间均匀分布的随机变量;KN为地表粗糙系数(一般可取0.004);F为扰动范围，m2;μ为相对高度的平均风速。

综上，风力机风速可表示为

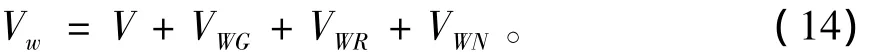
4 仿真研究

4.1 简单系统

图2是一个改进的IEEE 3机9节点系统［13］，其中一个区为无源负荷中心区。各发电机采用详细模型、计及励磁模型，负荷考虑恒阻抗特性。

4.2 不同风速情况下系统的相关性

4.2.1 含噪声风速情况

0.1 s时在G2上施加幅值标幺值为0.1的阶跃扰动。分别记录系统不加入风机和加入风机1～6 s的2种情况下所有发电机功率信号，这些信号经过相关性理论求取、计算，其相关系数如表1、表2所示。

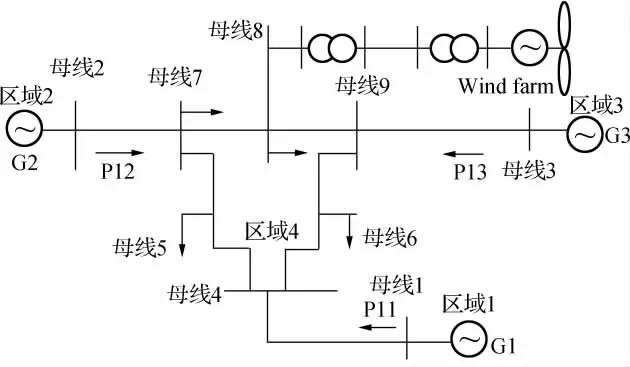
图2 改进的3机9节点系统示意图

表1 不含风电的有功功率的相关系数

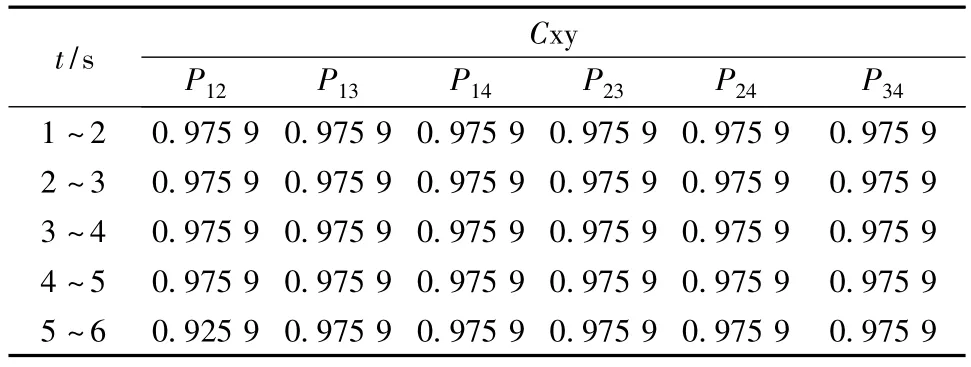
表2 含风电的有功功率的相关系数

由表1～表2可以看出，当在原系统中加入风机后，各个机组之间的相关程度被减弱了，可见风机的接入对系统造成了一定的影响。

4.2.2 含阵风情况

在风速为0～2 s幅值为5的阵风风速下的各发电机有功功率相关系数如表3所示。

表3 阵风时含风电系统有功功率的相关系数

由表3可以看出当在原系统中加入风机后各个机组之间的相关程度被减弱了。相比于噪声风速其影响更为严重。

4.2.3 含渐变风速情况

在风速为渐变风速下的各发电机有功功率相关系数如表4所示。

表4 渐变风时含风电系统有功功率的相关系数

由表4可看出当在原系统中加入风机后各个机组之间的相关程度被减弱了。但相比于其它风速其影响较为轻微。

4.2.4 含恒定风速情况

在风速为12 m/s恒定风速下的各发电机有功功率相关系数如表5所示。

表5 恒风速时含风电系统有功功率的相关系数

由表5可以看出，当在原系统中加入风机后，各个机组之间的相关程度也被减弱了，其影响较为严重。

4.3 风机接入不同地点对系统相关性的影响

0.1 s时在G2上施加幅值标幺值为0.1的阶跃扰动。分别记录风机接入不同地点即系统母线4、5、6、7、8、9时的情况。将记录的1～6 s的风机接入不同地点情况下所有发电机功率信号。经过相关性理论求取，计算它们之间的相关系数如表6所示。由表6可见，互相关系数Cxy清楚地表明了各发电机之间的相关性。

由表6可以看出，当在不同地点接入风机后，各个机组之间的相关程度不同，其对系统影响大小不同，当接入到母线5时，其影响较为严重，说明在母线5接入风机对系统影响较大且较恶劣。而在母线9接入时则相关系数比较大，说明风机在此处接入时对系统影响较小。

表6 风电接入不同地点的P24有功功率的相关系数

4.4 多个风场不同地点接入对系统相关性的影响

0.1 s时在G2上施加幅值标幺值为0.1的阶跃扰动。将容量相同的3个风场分别同时接入系统母线4、7、8，分别记录风机接入系统母线4、7、8时的情况。将记录的1～6 s的风机接入不同地点情况下所有发电机功率信号。经过相关性理论求取，计算它们之间的相关系数为0.998 7。可见，当多个风电场不同地点同时接入时对系统的相关程度影响较小，系统的相关程度较强，所以相关系数Cxy清楚地表明了各发电机之间的相关性。

5 结论

本文带着提高准确性的思考，从含风电接入的角度出发，提出了一种基于相关分析法快速估计含风电系统关联程度的方法。通过不同类型的风速模型的仿真算例对比，可以看出接入风机之后系统的关联程度被减弱了，不同风速类型对系统的影响不一致，而且风机接入不同地点对系统影响大小也不同。

［1］ 张卫红，于吉庆，王坤.新能源发电并网标准比较［J］.黑龙江电力，2011，33(6):403-408.

［2］ ROSS M.Wind Generation presents interconnection challenges［J］.North American Windpower，February，2006:55-58.

［3］ 王兴国，张举.基于相关分析和模糊推理的故障选相元件［J］.电网技术，2006，30(14):93-97.

［4］ 李伟，毕天姝，杨奇逊.基于相关分析的同杆双回线突变量选相新方法［J］.电力系统自动化，2011，35(8):58-62.

［5］ 成敬周，张举，陈琛，等.基于高频暂态分量进行相关分析及模糊推理的选相新方法［J］.电力系统自动化，2005，29(5):50-55.

［6］ 李岩，陈德树，袁荣湘，等.基于相关分析的暂态差动保护原理改进及仿真研究［J］.继电器，2003，31(2):64-68.

［7］ 虞瑄，程浩忠，王旭，等.基于相关分析的中长期电力负荷综合预测方法［J］.继电器，2005，33(15):49-52.

［8］ 徐群，陶顺，肖湘宁，等.新能源发电功率与电压偏差的相关性研究［J］.电测与仪表，2011，48(6):1-5.

［9］ 卢继平，丁然.计及风电场有功无功相关性的随机潮流计算［J］.微计算机信息，2010，26(31):159-161，158.

［10］马威，包广清.永磁直驱风电机组的建模与仿真［J］.工矿自动化，2010，36(8):49-53.

［11］尹明，李庚银，张建成，等.直驱式永磁同步风力发电机组建模及其控制策略［J］.电网技术，2007，31(15):61-65.

［12］严干贵，魏治成，穆钢，等.直驱永磁同步风电机组的动态建模与运行控制［J］.电力系统及其自动化学报，2009，21(6):34-39.

［13］韩松，徐政，武诚.利用相关分析的区间振荡振型快速估计方法［J］.高电压技术，2011，37(2):436-443.

［14］赵书强，范伟.由风力发电引起的电力系统强迫功率振荡［J］.华东电力，2009，37(1):98-102.

［15］李东东，陈陈.风力发电系统动态仿真的风速模型［J］.中国电机工程学报，2005，25(21):44-47.