基于TLS-ESPRIT 算法的电气化铁路谐波检测
李 强
0 引言
铁路电气化改造的逐步实施,武广、郑西、京沪等客运专线的开通,标示着中国铁路正快速迈入电气化时代。电气化铁路虽然在提高运行速度、增加运力等方面具有明显的经济、社会效益,但也同时带来了其他不利影响,其中,交-直型、大功率、单相整流电力机车所引起的谐波污染对公共电网及铁路沿线设备带来了严重危害[1~3],必须采取措施对其进行有效治理,而实时、准确的谐波检测是谐波治理的前提和主要依据。
目前,用于谐波检测的算法主要有:傅里叶变换、瞬时无功功率理论、小波变换、Hilbert-Huang变换、Prony 算法。傅里叶变换计算量大、实时性不够好、易产生频谱泄漏和栅栏效应;基于瞬时无功功率理论的方法不能对信号进行时间和频率联合检测;小波变换无法单独提取任意频次的谐波信号,且小波基系数受噪声影响大;Hilbert-Huang变换可以得到谐波的时频分布,但应用中存在端点效应,需做处理[4]。Prony 算法受噪声干扰、参数选择影响较大[5~6]。
1989 年,Roy 和Kailath 提出了一种新的信号参数提取算法—ESPRIT(Estimating Signal Parameter via Rotational Invariance Techniques)算法,它基于子空间技术,把待估计信号分解成信号子空间和噪声子空间,通过信号空间估计出信号参数[7~8]。具有优良的抗噪声性能、高分辨率、良好的参数适应性。ESPRIT 的思想是通过求旋转算子φ得出信号的衰减和频率,再由最小二乘(Least Square,LS)或总体最小二乘(Total Least Square,TLS)得出幅值和相位[9]。
TLS - ESPRIT(Total Least Square - Estimating Signal Parameter via Rotational Invariance Techniques)是振荡衰减正弦信号参数辨识、谐波恢复的有效工具[8]。目前已被广泛应用于雷达阵列信号、语音信号、生物信号处理等场合,也正逐渐被引入到电力系统领域,如电压闪变参数提取、低频振荡模式分析[8~11]。本文将TLS-ESPRIT 算法引入到电气化铁路谐波检测中,从而为治理电气化铁路谐波污染奠定基础。
1 TLS-ESPRIT 算法[8,11]
设信号x(n)由p 个幅值按指数函数变化的正弦分量和白噪声组成,在采样时刻n,可表达如下:

ESPRIT 算法可由构造观测数据自相关和互相关矩阵、进行特征值、奇异值分解来实现,具体过程参见文献[9]和[12]。由于该方法计算量较大,本文将通过由采样数据序列构造Hankel 矩阵来实现该算法,计算简单、快捷、易于实现。
设有n 个采样数据序列x(0),x(1),x(2),…x(n-1),构造r×m 阶Hankel 矩阵如下:

式中,r>p,m>p;且满足:r + m -1 = n。
对H 矩阵进行SVD 分解,有:
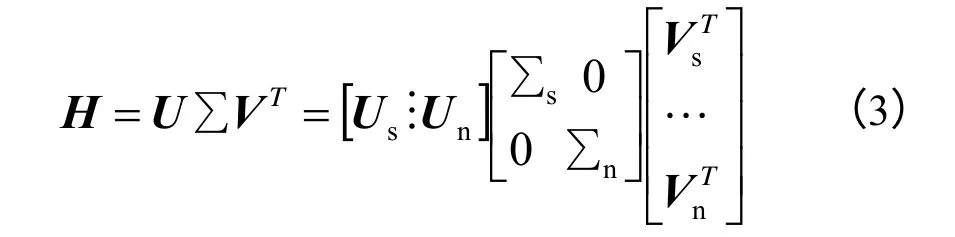
式中,U 为r 阶正交矩阵;∑为r×m 阶对角阵,其对角元素由矩阵H 的奇异值作递减排列得到;V为m 阶正交矩阵,Vs、Vn分别与信号子空间和噪声子空间对应。
令Vs作式(4)分解:

则存在可逆阵P,使得[8,11]:

求出P 的特征值即可估计出各信号分量的衰减和频率[11],这可由总体最小二乘法(TLS)实现。
令K = [V1,V2],对K 做SVD 分解,即K =,其中,将V3分块成4 个p×p的子矩阵,有:

则式(5)的总体最小二乘解为

求得Ptls的特征值λi(i = 1,2,…p),则式(1)信号中所包含的各正弦分量的衰减因子、频率计算:
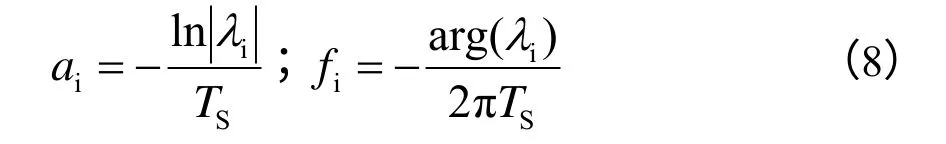
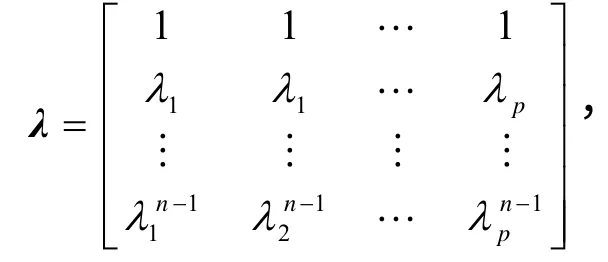
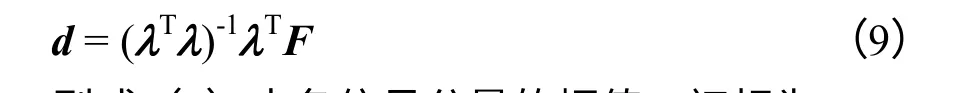
则式(1)中各信号分量的幅值、初相为

至此,信号分量的各参数均已求出。
2 评价指标与计算步骤
2.1 评价指标
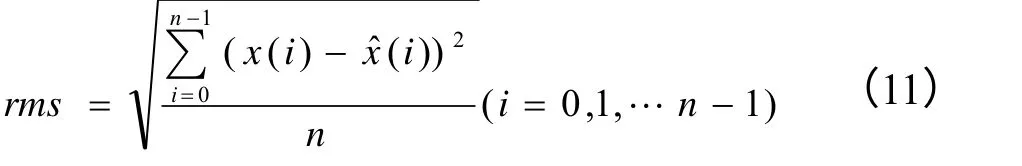
rms 反映了拟合模型输出数据偏离原始采样数据的程度,可作为拟合衡量指标。无噪声干扰下,其值越小,拟合效果越好,当rms = 0 时,拟合曲线和原始曲线完全重合;有噪声时,该值则与噪声的均方差接近。
2.2 TLS-ESPRIT 计算步骤
TLS-ESPRIT 算法的完整实现步骤如下:
(1)由测量、记录装置或时域仿真获得采样数据序列X = [x(0),x(1),x(2),…x(n-1)]。
(2)由式(2)构造r×m 阶Hankel 矩阵H。
(3)按照式(3)对H 进行SVD 分解,并将右奇异向量V 分解成信号子空间Vs、噪声子空间Vn。
(4)由式(4)分解Vs,得到矩阵V1、V2。
(5)由式(6),式(7)求得Ptls的特征值λi(i= 1,2,…p),再按照式(8)求出各分量的衰减因子ai、频率fi。
(6)根据式(9),式(10),求出各分量幅值ci、初相φi。
(7)由式(11)评价拟合结果、做辅助分析。
3 电气化铁路谐波
3.1 谐波产生原因
国内电气化铁路采用工频交流50 Hz三相供电单相用电,其牵引网供电电流为单相交流的电力牵引电流制,这种电流制在电力机车上将交流电降压后整流以供应直流牵引电动机[2~4]。因此,当三相电力系统向电气化铁路牵引负荷供电时,电力机车可看作是波动性很大的大功率单相整流负荷,这种高压单相非线性负载,将会产生大量谐波,并作为谐波源,注入电网中,造成系统波形畸变,严重影响供电质量、输电效率和用电设备的使用寿命。
3.2 电气化铁路谐波特点
(1)电力机车产生的谐波源具有基波能量很大,其他各次谐波能量相对较低(主要是3 次、5次、7 次、11 次谐波)等特点。
(2)交流侧电流波形为镜对称,不含偶次谐波。
(3)谐波含量会随机车型号、数量、分布和运行工况而有较大的变化。电气化铁道谐波比其它非线性负荷引起的谐波更为复杂。
(4)由于电力机车的功率大,速度、负载状况变化频繁,因此牵引电网谐波含量高,同时还伴随有负序电流。
4 仿真测试
本文根据 2.2 节的计算步骤编写了TLS-ESPRT 算法计算程序。由电气化铁路谐波特点,构造了谐波信号,并进行以下仿真测试,以研究算法辨识电气化铁路谐波的性能。
4.1 模式辨识
若某信号解析表达式为
y = 100exp(-0.2t)cos(2π×50t + π / 6) +2exp(-1.5t)cos(2π×250t + π / 5) + 5exp(-t)cos(2π×550t + π / 7) + 3exp(-4t)cos(2π×370t + π / 8) (12)
该信号含基波、2 个谐波、1 个间谐波模式,取采样频率为 1 500 Hz,时间窗为 0.1 s,TLS-ESPRIT 对该信号的辨识结果和拟合曲线分别如表1 和图1 所示。

表1 TLS-ESPRIT 算法对测试信号各模式的辨识结果表
表1 说明,在选取合适的采样频率和时间窗参数下,TLS-ESPRIT 算法能准确辨识出基波、各次谐波、间谐波模式,分量5 由于其幅值接近于0,可忽略该分量。均方根接近于0,拟合曲线和实际曲线几乎完全重合,说明TLS-ESPRIT 算法辨识谐波模式非常准确。
4.2 频率分辨率
设信号解析表达式如式(13)所示:
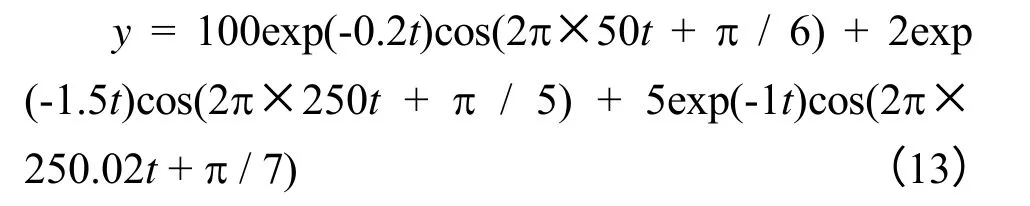
式(13)中,含基波和2 个频率相差0.02 Hz的谐波模式,TLS-ESPRIT 对该信号的辨识结果和拟合曲线如表2、图2 所示。

图1 实际曲线及TLS-ESPRIT 辨识曲线图

图2 实际曲线及TLS-ESPRIT 辨识曲线图

表2 TLS-ESPRIT 算法对频率相近谐波信号辨识结果表
可见,利用TLS-ESPRIT 算法可分辨出频率差为0.02 Hz 的谐波分量(分量4 可忽略,解释同上),具有较高的频率分辨率,这对谐波测量意义重大。
5 结论
本文将TLS-ESPRIT 算法应用到电气化铁路谐波检测中,详细阐述了其算法原理、评价指标、计算步骤。用编写的TLS-ESPRIT 算法程序对信号测试表明:在合适的采样频率和时间窗长度下,TLS-ESPRIT 算法能准确识别出各次谐波、间谐波模式,具有较高的频率分辨率。进而为进一步治理电气化铁路谐波奠定了基础。当然,TLS-ESPRIT算法辨识参数选择、抗干扰问题也较为重要,这是本文的后续研究工作。
[1] 林海雪,周胜军.电气化铁路的谐波标准问题[J].中国电力,1999,32(9):55-58.
[2] 孙卓,姜新建,朱东起.电气化铁路中谐波、无功、负序电流的实时检测方法[J].电力系统自动化,2003,27(15):53-57.
[3] 李群湛.电气化铁道并联综合补偿及其应用[M].北京:中国铁道出版社,1993.
[4] 苏玉香,刘志刚,李科亮,等.基于HHT 方法的电气化铁道谐波检测与分析[J].铁道学报,2009,31(6):33-38.
[5] 丁屹峰,程浩忠,孙毅斌,等.基于小波变换和Prony算法的间谐波参数辨识[J].上海交通大学学报,2005,39(12):2083-2087.
[6] D J Trudnowski,J M Johnson,J F Hauer.Making prony analysis more accurate using multiple signals[J].IEEE Transactions on Power Systems,1999,14(1): 226-231.
[7] Roy R,Kailath T.ESPRIT:estimation of signal parameters via rotational invariance techniques[J].IEEE Trans on Acoust Speech and Signal Processing,1989,37(16):297-301.
[8] 张静,徐政,牛卢璐.TLS-ESPRIT 在电力系统信号高精度频谱估计中应用[J].电力自动化设备,2009,29(5):48-51.
[9] 祝磊.电力系统信号参数提取的TLS-ESPRIT 算法应用研究[D].吉林:东北电力大学,2009.
[10] 李天云,祝磊,党国营,等.总体最小二乘—旋转矢量不变技术在电压闪变参数提取中的应用[J].电网技术,2009,33(13):58-63.
[11] 张静,徐政,王峰,等.TLS-ESPRIT 算法在低频振荡分析中的应用[J].电力系统自动化,2007,31(20).
[12] 马秉伟,周莉.基于TLS-ESPRIT 算法和支持向量机的间谐波检测[J].高电压技术,2009,35(6):1468-1471.

