Study on Stable Scanning of Terminal Sensing Ammunition Based on Quaternion Transformation
LI Chen-ming(李臣明),LIU Yi-xin(刘怡昕)
(Nanjing Artillery Academy of PLA,Nanjing 211132,Jiangsu,China)
Introduction
The terminal sensing ammunition,shorten as TSA,is a kind of smart ammunition which can make indirect aiming weapons attack on the enemy’s cluster armored targets in long distance.Experts and scholars researched the terminal sensing ammunition deeply because of its unique combat features.LIU Shi-ping presented its revolving parachute-bullet resistance model[1].SHU Jing-rong conducted theoretical analysis and numerical simulation for the parachute-bullet system motion[2]and studied the scanning motion of terminal sensing ammunition with flexible single wing[3].However,in all these studies,Euler motion equations are used to establish the terminal sensing ammunition’s kinetic equations.Three Euler angles are used to describe its revolving attitude.The shortcoming of the method is that the kinetic equations show singularity when the attitude angle is uncertainty or large and there are singular points in calculation,thus,this method is not suitable to describe large scope attitude motion.
In this paper,quaternion is used to transform the kinetic equations to describe the revolving of terminal sensing ammunition and avoid singular points in uncertainty or large attitude angle.
1 Transformation of Kinematics Equations Based on Quaternion
1.1 Advantages of Quaternion
The earth inertial coordinate system Cixiyizi,the fixed coordinate system Caxayazaof parachute and the fixed coordinate system Cbxbybzbof shell-body are defined respectively.
Three Euler angles θb,ψb,φbare often used to describe kinetic features of terminal sensing ammunition[4].

where θbis the rotation angle between axis of shell and vertical axis,ψbis the precession angle,φbis the angle of rotation,ω is the angular velocity.
If Euler equations are expressed in matrix,the sinusoid function about attitude angle will exist in denominator.The singular points will emerge when the angle reaches to 90°,and it leads to degradation of equation.The quaternion is a better method to describe the revolving motion of rigid body in large scope and avoid the degradation.
The quaternion is a super-complex including a real number unit“1”and three imaginary number units“i1,i2,i3”,to extend three-dimensional vector algebraic operation to multiplication and division.It can be expressed as

and
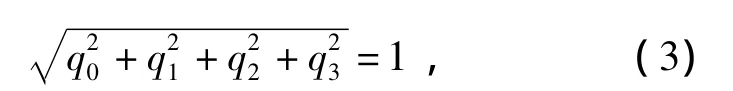
where q0is the real number part or the scalar part of quaternion and q1,q2,q3are all real numbers.When the quaternion is used to describe the revolving motion,any parameter will not degrade while the calculation of trigonometric function also can be reduced and the operation speed and the accuracy will increase.For the terminal sensing ammunition with parachute,in initial phase when bullets are projected from shell to start to scan,the swing angle may reach to 90°under the influence of environment and disturbance;therefore,the quaternion can be used to avoid singular points in calculation.
1.2 Kinetic Equations Based on Quaternion Transformation
Euler kinetic equations can be expressed by using the quaternion as

Because integral error damages the orthogonality of quaternion transformation and leads to the norm of quaternion not equal to 1,the norm needs to be corrected as follows.
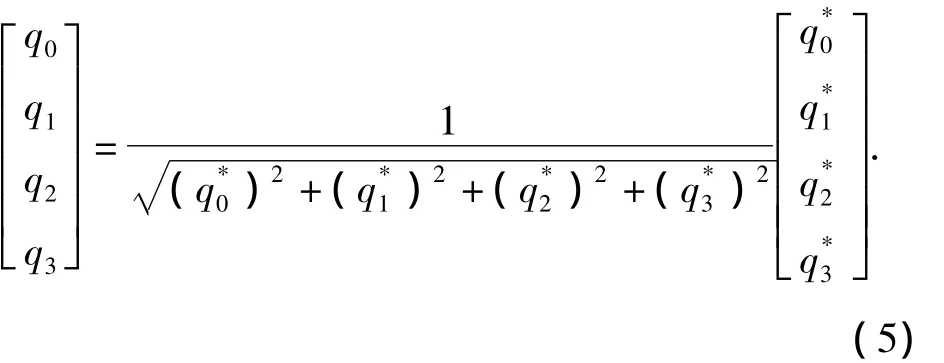
The revolving kinetic equations for rigid body are composed by the Eq.(4 -5).It is a group of nonsingular linear differential equations.The equations meet link equation with the norm of 1 under circumstance of orthogonal transform.Compared with the other rigid body revolving kinetic equations,their features are as follows.
1)It is a group of nonsingular linear differential equation without singular points and different from the revolving equations expressed in Euler angle.
2)Compared with direction cosine,the quaternion has the least numbers of nonsingular parameters and link equations.By formal operation of quaternion,the orthogonal transform operation can be given by means of single value.
3)Two important physical quantities describing motion of rigid body,i.e.,angular velocity(revolving features of rigid body)and limited revolving vector(position features of rigid body),can be expressed by quaternion in the only form.These two quantities are expressed by using instantaneous Euler revolving vector and equivalent Euler revolving vector,respectively.
4)The quaternion can use super complex space element to express Euler revolving vector.The super complex space is the counterpart of three-dimensional real number space.
1.3 Angle Transformation Based on Quaternion
Although the revolving kinetic equations in the form of quaternion is not expressed by using Euler angle and its derivative,the angle geometrical relation equation still includes Euler angle.Therefore,the relation between quaternion and attitude angle needs to be determined in order to transform angle in calculation.
The transformation matrix expressed by Euler angle between body and earth coordinate systems is

The matrix can be expressed in quaternion as

Because[B]=[B]1and corresponding elements are equal,we have

2 Ballistic Model Based on Quaternion Transformation

The simultaneous differential equations of the terminal sensing ammunition based on the quaternion transformation can be expressed as where θris the increment of scanning angle,θ the angle between axis Ctztof shell and rigid body axis Cpzpof parachute;Hpx,Hpyand Hpzthe expressions in Ref.[4];Aijthe transformation matrix between parachute-attached coordinate system and earth inertial coordinate system;Cijthe transformation matrix between parachute-attached coordinate system and body-attached coordinate system(i=1,2,3;j=1,2,3);FAzithe total aerodynamic force,FAyithe resistance,FAxithe lift force;mpthe mass of parachute,mbthe mass of body;l1the characteristic length of parachute canopy,ld1the distance between mass centre of parachute and mass centre of hinge column,ld2and ld3the coordinates y and z of mass centre of hinge column in body-attached coordinate system,Apand Abthe equatorial inertia moments of parachute and body,Cpand Cbthe polar inertia moments of parachute and body,ωpiand ωbtthe angular velocities of parachute and body,g the acceleration of gravity.
3 Simulation and Analysis
In order to validate the correctness of Eq.(9),both Euler equations and equations transformed by using quaternion are used separately in programming and simulation.The curves about falling speed,rotational speed,scanning angle and scanning track can be obtained,as shown in Fig.1 - 5.Suppose the ejection height of two models is 700 m and the static hanging angle of the body,i.e.initial ballistic obliquity,equates to 10°only in Euler equations.In quaternion model,the static hanging angle is taken as 27°to exam whether there exists the singular points when the angle reaches to 90°.
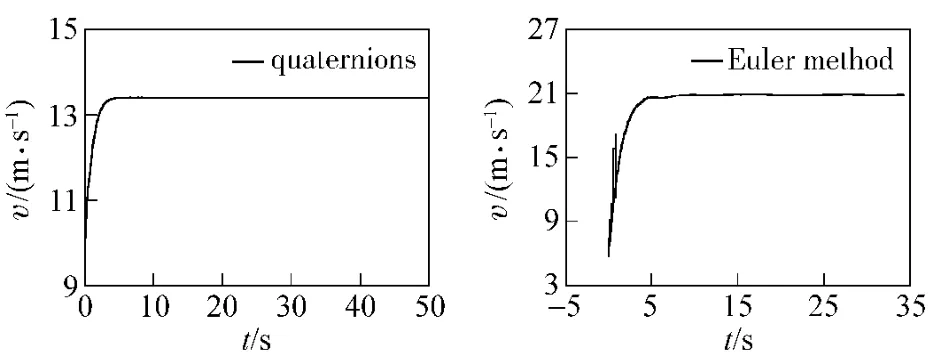
Fig.1 Falling speed vs.time
From Fig.1 - 3,it can be found that the falling speeds of both models tend to be stable after 3.8 s;the rotational speed obtained from quaternion model reaches to 3.9 rad/s and stabilizes at 5.5 s while the speed obtained from Euler equation reaches to 9.8 rad/s and stabilizes at 5.3 s;and the stable time of scanning angle obtained from quaternion model is 11.7 s while stable time obtained from Euler equation is 12 s.That is to say,from two models,the close results can be obtained.
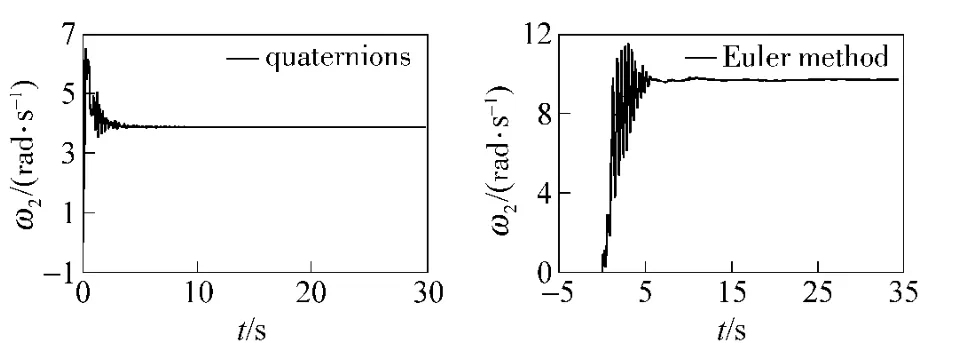
Fig.2 Rotational speed vs.time
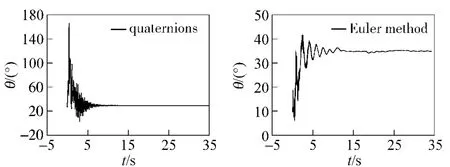
Fig.3 Scanning angle vs.time
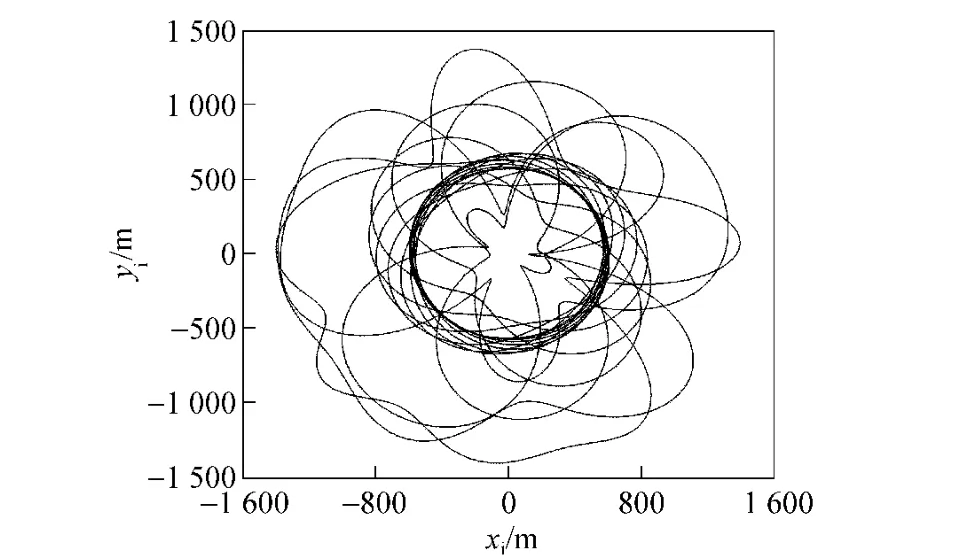
Fig.4 Scanning track from 0 -10 s
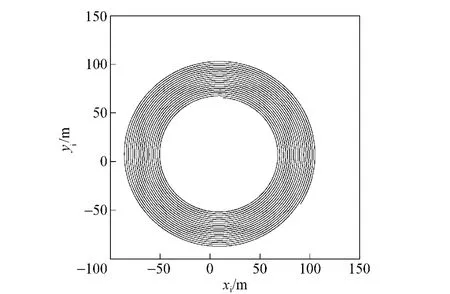
Fig.5 Scanning track from 40 -45 s
The parameter best reflecting the difference be-tween both models is the change of scanning angle.Fig.3 shows that the scanning angles obtained from both models can converge quickly and stable times are about 10 s.However,in the results of quaternion model,the peak scanning angle can reach to 166.3°and does not diverge.It means that the singular points do not emerge when scanning angle equates to 90°.Fig.4 - 5 show that,from 0 -10 s,the scanning is relatively disordered in large scope,the uncertainty of attitude angle is strong,and the scanning becomes been very stable from 40-45 s.That is because the initial static hanging angle is larger and the swing of body is too big.With the swing tends to stable,the scanning track tends to normal also.
The simulation results show that it is correct and reliable to describe static scanning motion of terminal sensing ammunition by using quaternion;the calculated data reflects the physics law of its static scanning;the scanning track can be formed and the quaternion model is better than Euler model.
4 Conclusions
In order to resolve the problem that the singular points emerge in calculation when Euler angles are used in the ballistic equations of terminal sensing ammunition,the quaternion is use to transform Euler equations.The transformed model and the original model are compared by using simulation.The simulation results show that the singular points will not emerge in the calculation of transformed model based on quaternion,the scanning track can be formed correctly and reliably,and the quaternion is more suitable than Euler model for describing big attitude angle motion of terminal sensing ammunition.
[1]LIU Shi-ping,HAN Zi-peng.The study on rotary parachute-body resistance model of terminal sensing ammunition[J].Acta Armamentarii,1997,18(3):221 - 225.(in Chinese)
[2]SHU Jing-rong,WANG Bao-gui,HAN Zi-peng.The analysis on triplicity motion of terminal sensing ammunition system[J].Journal of Aeronautics,2001,22(6):481-485.(in Chinese)
[3]SHU Jing-rong.The study on the large angle of attack scanning characteristic of asymmetric terminal sensing submunition and its application[D].Nanjing:Nanjing University of Science and Technology,2004:70 - 71.(in Chinese)
[4]LIU Yi-xin,LIU Yu-wen.Exterior ballistics[M].Beijing:Tide Book Concern,1998.(in Chinese)
- Defence Technology的其它文章
- Research on Coordinated Antisumarine Attack Effeciency of Two Helicopters Under Countermeasures
- Experimental Study on Plasma Temperature of Semiconductor Bridge
- Design of ANSYS-based Cathode with Complex Groove
- Experimental Investigation on Space-dispersed Double-wall Jet Combustion System for DI Diesel Engine
- Research on Three-Echelon Inventory Model and Algorithm for Valuable Spare Parts in Weapon Equipment
- Experimental Research on Influence of Some Factors on Ejection Height of Cargo Projectile

