不同梯度温度作用下曲线桥梁的温度效应分析

何 翔， 方诗圣， 方 飞， 张 鲲， 王 伟

（1.合肥工业大学 土 木与水利工程学院，安徽 合 肥 230009；2.安徽省交通规划设计研究院，安徽 合 肥 230088）

混凝土曲线桥梁在太阳日照的影响下，由于混凝土导热系数较低，沿高度方向各纤维层的温度是不同的，因而形成竖向梯度温度模式，梯度温度作用在桥梁结构内部将产生较大的温度应力，这会影响到桥梁结构的安全性和耐久性［1－3］。

文献［4］采用实验测定和数值模拟等方法，分析了太阳日照影响下的温度模式，并分析了桥梁方位角、翼缘长度等参数对温度模式的影响；文献［5］分析了在日照温度作用下，支承方式、悬臂长度与腹板厚度之比、顶板厚度与腹板厚度之比、曲率半径等参数对曲线桥梁力学性能的影响；文献［6］分析了不同的梯度温度作用分布对直梁桥力学性能的影响。

现阶段关于温度作用对小半径曲线桥梁影响的研究主要关注以下2点：① 截面形式多为单箱单室的箱形梁、T型梁和变截面梁；② 在荷载形式上则主要利用现场试验所采集的数据，通过温度扩散理论进行推导或者数值模拟得到的，温度场模式单一。而不同温度模式的温度作用对曲线桥梁的力学性能影响分析研究较少。本文在前人研究的基础上，选择曲率半径作为关键参数，并综合各国规范规定的梯度温度模式，分析不同温度模式对混凝土曲线箱梁桥空间力学性能影响的区别。分析结果表明，新西兰规范规定的升温梯度作用下的径向拉应力最大，英国规范和中国公路规范规定的降温梯度作用下的应力最大，不同曲率半径下曲线梁桥受温度荷载的横桥向正应力变化较大。

1 温度作用理论与工程概况

混凝土箱形截面受太阳照射后，其向阳表面（顶板或腹板）的温度变化幅度大，其背阳表面（腹板、底板）的温度变化幅度小，且沿高度方向各纤维层的温度是不同的，从而产生所谓的温度梯度。由于结构材料热胀冷缩的性质，势必产生温度变形，对于闭合箱形截面的梁，在横截面上会产生如图1所示的变形形式。如果箱梁采用了如图1所示的约束形式，梁体支座还会在平面内产生方向相反的支反力。实际上，对于连续曲线箱梁桥，温度梯度的作用形式不仅仅表现在梁的纵向，在梁的横向和竖向也表现出很明显的特征。箱梁顶板或腹板受太阳照射，产生温度梯度，会使得弯箱梁产生竖向挠曲和扭转变形。一般地，当梁的曲率半径越大，或者说越接近直桥时，则弯箱梁在日照温差的作用下，越来越表现出纵桥向的变形特征；当曲线梁曲率半径越小，则弯箱梁越来越表现出横桥向或竖向的变形特征。

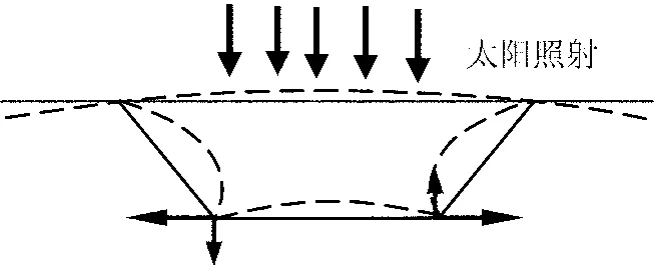
图1 箱型截面在日照温差影响下的变形

本文所依托实际工程的概况如下：某一座3联匝道桥，曲率半径为195m，其中第1联和第3联的上部结构采用预应力混凝土现浇连续曲线箱梁，跨径5×25m；第2联上部结构采用先简支后连续预应力混凝土预制箱梁，跨径（30＋2×25＋30）m。

2 模型建立

2.1 模型参数

本文针对实际工程的第3联建立了空间有限元模型，几何模型的建立过程和方法是按照“点生线，线生面，面生体”的方法来建立的。该桥第3联的平面图如图2所示。

主梁截面采用单箱双室结构，底面宽6.5m，桥面宽10.5m，高1.5m，支座处和跨中主梁截面如图3所示，图中尺寸单位均为cm。

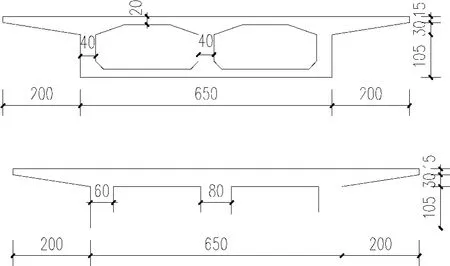
图3 匝道桥第3联横截面图

模型采用20节点二次六面体单元（C3D20R）和10节点二次四面体单元（C3D10M）混合建模，跨中处等截面段采用C3D20R单元，支座处变截面段采用C3D10M单元，共划分为423 785个单元，如图4所示。

采用的材料力学与热力学参数见表1所列。

荷载及边界条件：考虑温度作用对曲线桥梁的影响，因此忽略重力、车辆荷载和预应力等外加荷载，只考虑温度作用，支座采用点支承，按设计规定确定约束方向。

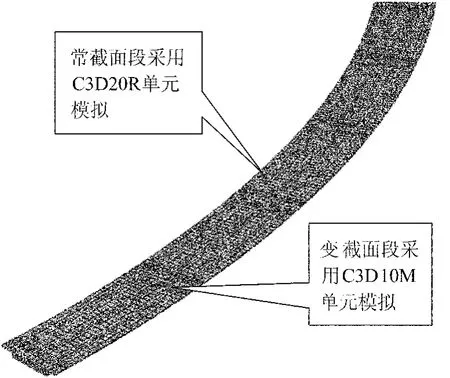
图4 梁体网格划分图

表1 材料的力学及热力学参数

混凝土与钢筋的接触采用分离建模、组合固定的方法，即钢筋与混凝土独立建模，建模完成后，通过位移约束的方式建立黏结，不考虑黏结滑移。

在分析曲率半径对温度应力的影响时，分别建立了曲率半径R为60、100、195m的有限元模型，其主梁梁长等主要参数不变，仅修改曲率半径。

2.2 温度作用模式

为了分析不同温度作用模式对曲线桥梁力学性能的影响，拟采用不同规范所规定的温度作用模式加载，规范温度作用模式简介［7－11］见表2所列。

表2 各国规范温度梯度曲线的简要介绍

基于本工程的结构形式，各国规范温度梯度取值如图5所示，初始温度t1＝0℃，长度单位为cm。

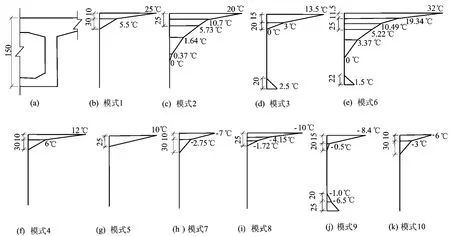
图5 箱梁温度梯度曲线计算图式

3 计算结果及分析

将上述不同工况的温度梯度曲线施加于图2所示的现浇箱梁中，采用空间有限元计算方法分析，得到应力分析结果如下。

3.1 横向应力分布

为了分析梯度温度作用对曲线桥梁横截面上应力分布的影响，选择1跨跨中作为控制截面，计算桥梁结构在温度作用下的横向应力分布。

曲线桥梁受梯度温度效应作用时的横向应力分布如图6和图7所示。

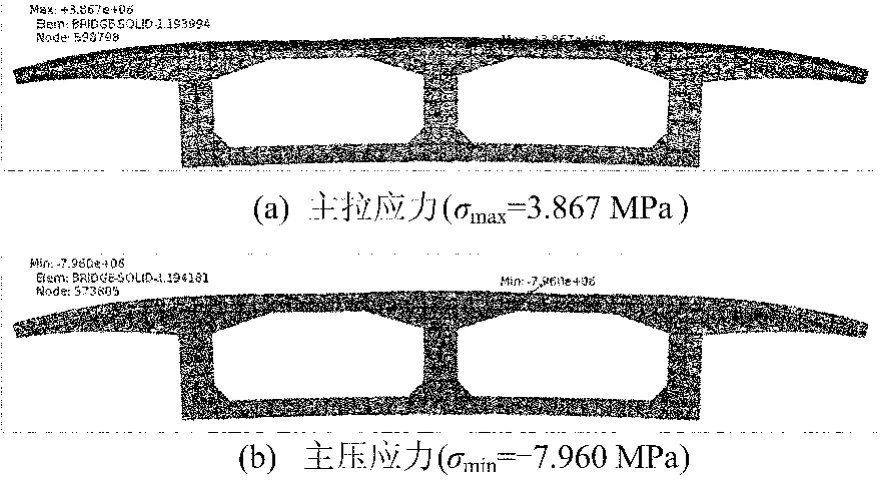
图6 升温梯度温度效应作用下的跨中应力分布

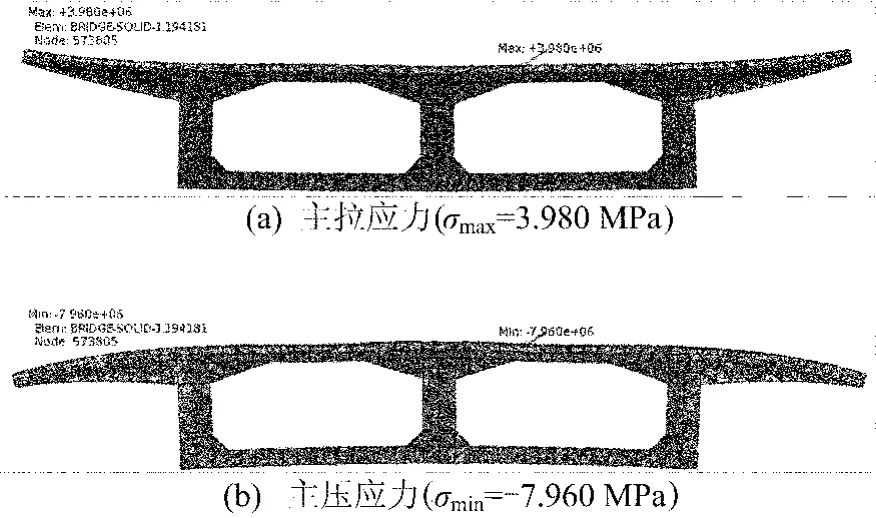
图7 降温梯度温度效应作用下的跨中应力分布

从图6和图7可知，单箱双室箱梁结构在温度梯度作用下主应力竖向分布符合理论分析的结论：箱梁顶板和翼缘板上边缘受拉，下边缘受压；腹板和底板上边缘受压，下边缘受拉。温度应力的横向分布不均匀，在中腹板与顶板交接处主应力较大（以下简称交接处），在降温梯度作用下，交接处外壁混凝土出现主拉应力极值，方向为顺桥向，交接处内壁混凝土出现主压应力极值，方向为横桥向；在升温梯度作用下，交接处外壁混凝土出现主压应力极值，方向为顺桥向，交接处内壁混凝土出现主拉应力极值，方向为横桥向。

从以上分析可以看出，温度作用效应不可忽视，在设计温度梯度效应作用下，若不对箱梁施加横向预应力，则箱梁顶板的底面将因受拉而出现裂缝。

3.2 不同温度梯度模式对主应力的影响

曲线桥梁受不同温度梯度模式影响时的主应力变化如图8和图9所示，其中横轴1～10表示模式1～模式10。

升温时的箱梁顶板上边缘，对于最大拉应力，采用新西兰规范规定的温度梯度模式计算结果较大，达5.35MPa；对于最大压应力，采用中国公路桥涵规范［7］规定的温度梯度模式计算结果较大，达7.96MPa。降温时的箱梁顶板上边缘，对于最大拉应力，采用中国公路桥涵规范［7］规定的温度梯度模式计算结果较大，达3.98MPa；对于最大压应力，采用英国规范［10］规定的温度梯度模式计算结果较大，达2.34MPa。从上述分析可知，主拉应力的方向是横桥向，主压应力的方向是顺桥向。

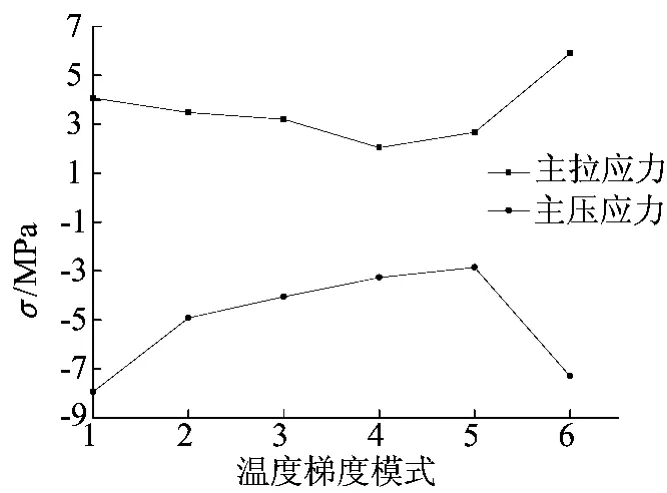
图8 升温作用下主梁1跨跨中应力变化曲线

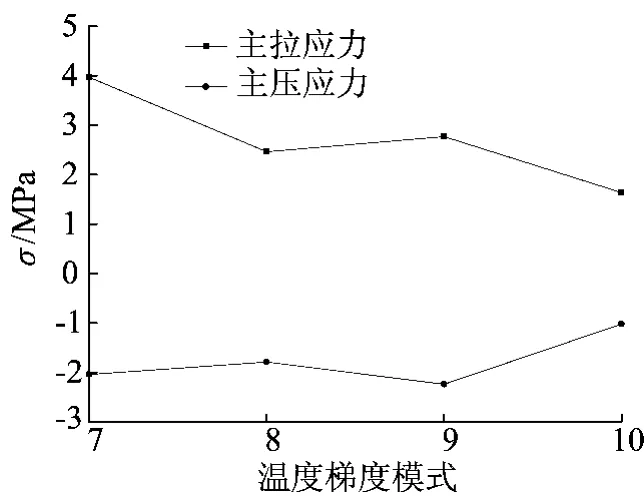
图9 降温作用下主梁1跨跨中应力变化曲线

因此，实际结构设计时，为了有效控制温度应力，确保结构安全，分析升温温度梯度效应作用对横桥向配筋的影响时，应选择新西兰规范作为控制标准；在分析降温温度梯度效应作用对横桥向配筋的影响时，应选择中国公路规范作为控制标准；分析升温温度梯度效应作用对顺桥向配筋的影响时，应选择中国公路规范作为控制标准；在分析降温温度梯度效应作用对横桥向配筋的影响时，应选择英国规范作为控制标准。

3.3 不同曲率半径对主应力的影响

不同曲率半径的曲线桥梁受不同温度作用模式影响时的主应力变化见表3和表4所列。

从表3和表4可知，不同的温度梯度受曲率半径的影响是不同的，升温时温度梯度对主拉应力影响较大，其中模式6的影响最大，达1.104 1倍；降温时温度梯度对主压应力影响较大，其中模式8的影响最大，达1.081 1倍；不同的曲率半径对温度作用效应的影响很大，曲率半径越小时，应力越大，曲率半径为60m时的应力变化达到10%，不可忽略。因此，在实际结构设计时，应根据曲率半径的不同，对温度作用应力结果适当放大，以确保结构受力安全，具体系数可以参考表3和表4。

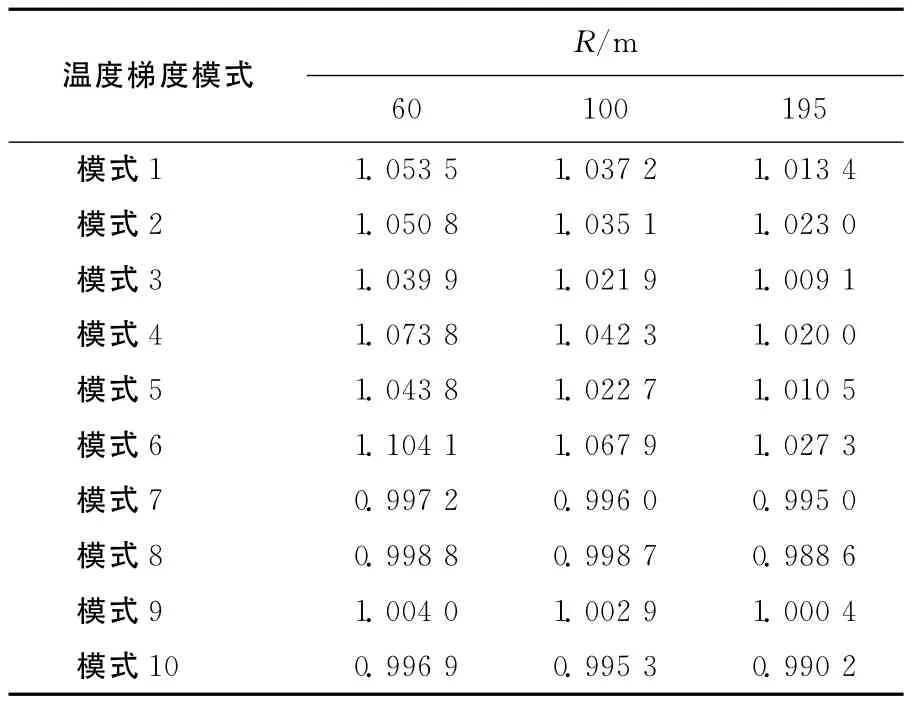
表3 不同半径相对于直桥的主拉应力比值

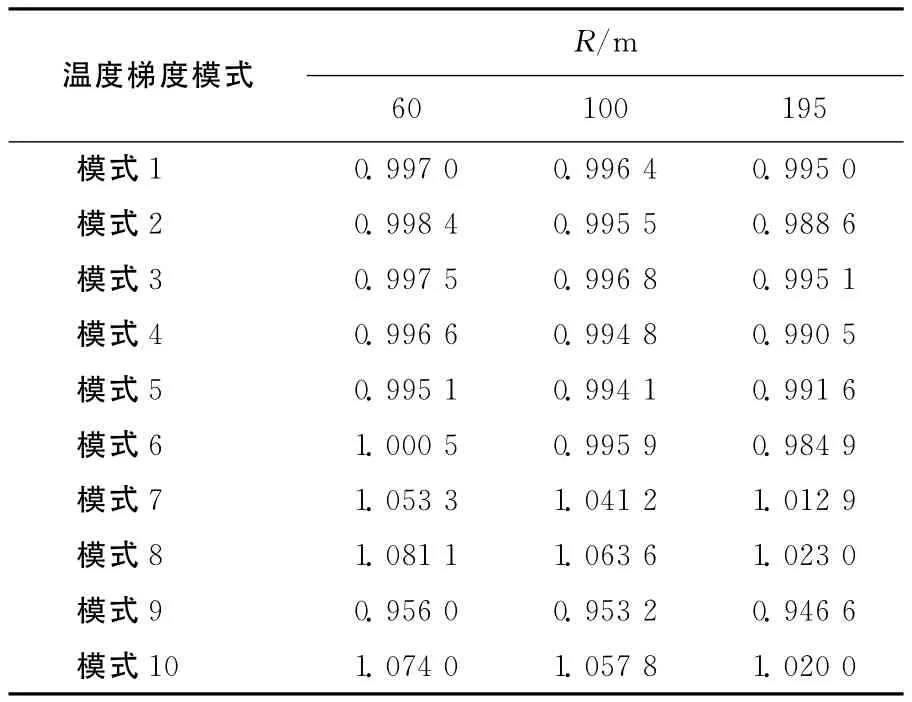
表4 不同半径相对于直桥的主压应力比值

4 结 论

（1）温度作用效应不可忽视，在设计温度梯度效应作用下，若不对箱梁施加横向预应力，则箱梁顶板的底面将因受拉而出现裂缝。

（2）在升温温度梯度效应作用下，截面的最大拉应力出现在箱梁顶板的下边缘，同时，箱梁顶板的上边缘将出现最大的压应力。在降温温度梯度效应作用下，截面的最大拉应力出现在箱梁顶板的上边缘，同时，箱梁顶板的下边缘将出现最大的压应力。

（3）采用不同的温度梯度模式对温度应力计算结果影响较大。升温时的箱梁顶板上边缘最大拉应力，采用新西兰规范规定的温度梯度模式计算结果较大；降温时的箱梁顶板上边缘最大拉应力，采用英国规范和中国公路规范规定的温度梯度模式计算结果较大。因此，实际结构设计时，建议在分析升温影响时，选用新西兰规范作为控制标准，而在分析降温影响时，综合考虑中国公路规范和英国规范的计算结果，从而有效控制温度应力，确保结构安全。

（4）曲率半径对温度作用效应分析影响比较大，特别是腹板和顶板交接处，为了保证结构受力安全，在曲线梁桥结构设计时，适当放大温度作用应力。

［1］ 龙佩恒，陈惟珍.温度应力对既有混凝土连续箱梁桥开裂的影响分析［J］.公路交通科技，2007，24（3）：68－71.

［2］ 曾庆响，韩大建，马海涛，等.预应力混凝土箱梁桥的温度效应分析［J］.中 南大学学 报：自然科 学 版，2010，41（6）：2360－2366.

［3］ 肖星星.年温差对多跨长联桥的影响分析［J］.合肥工业大学学报：自然科学版，2008，31（4）：639－644.

［4］ 汪 剑，方 志.混凝土箱梁桥的温度场分析［J］.湖南大学学报：自然科学版，2008，35（4）：23－28.

［5］ 苏 丹.温度场及温度应力对曲线箱梁桥受力性能的影响研究［D］.北京：北京交通大学，2007.

［6］ 吕 婷，刘 静，葛胜锦.混凝土梁桥的温度应力分析及梯度选择［J］.中外公路，2009，29（3）：337－343.

［7］ JTG D60－2004，公路桥涵设计通用规范［S］.

［8］ TB 10002.3－2005，铁路桥涵钢筋混凝土和预应力混凝土结构设计规范［S］.

［9］ AASHTO，美国桥梁设计规范：荷载与抗力系数设计法［S］.

［10］ BS 5400，钢桥、混凝土桥及结构桥［S］.

［11］ 刘兴法.混凝土结构的温度应力分析［M］.北京：人民交通出版社，1991：53－60.