随机粗糙面上电磁散射的高效迭代IEM计算

张晓燕，李 子，江代力，刘志伟

（华东交通大学信息工程学院，江西南昌 330013）

复合目标电磁散射特性的研究，对雷达图像解读、雷达体制研制都具重要意义。然而，目标与环境间的相互作用十分复杂，其耦合场的计算非常耗时，计算量随目标尺寸和粗糙面作用区域的增加而急剧增大，是制约算法的主要瓶颈。研究粗糙面散射近场的高效计算方法对进一步建立高性能的复合目标电磁散射算法，研究复杂环境下目标电磁散射特性具有重要意义。

目前，计算粗糙面散射场的方法有数值法和解析法。数值法如矩量法（MoM）［1-2］精度高，但计算复杂、速度慢，受计算机计算能力的影响，粗糙面与目标复合散射数值模拟理论和方法的研究对象主要集中于粗糙面为一维的二维复合目标散射问题，或者是粗糙面尺寸不超过30λ×30λ（λ代表波长）的三维复合目标电磁散射问题［3］，而在电大尺寸复合目标的散射计算中，粗糙面的尺寸往往高达成百上千λ2。相比之下，解析法如基尔霍夫近似法（KA）［4］、物理光学法（PO）［5］等的精度较低，但由于运算量小、速度快，在研究粗糙面散射远场特性时还可进一步简化为近似的数学表达式，常被用来研究粗糙面的散射远场特征。1975年，G.A.Thiele等［5］提出了解析法与数值法相结合的混合算法思想，其后混合法一直在不断发展，在提高算法效率上取得了显著的效果。2008年，金亚秋等人提出了混合基尔霍夫近似法和矩量法（KA-MoM）［6］，实现了一般粗糙面（例如：土壤、海洋）上目标电磁散射的高效计算。但KA法只适用于粗糙度较低的光滑型大尺度粗糙面，当粗糙度较大时，则应使用微扰法（SPM）［7］，或者是更为精确的数值算法，而实际中，在不同频率的雷达波照射下，粗糙面也会具有小尺度或者双尺度粗糙面统计特征。1992年，Fung等人结合KA和SPM法，提出适用范围更广的积分方程法（IEM）［8］，应用于水域反演［9］等。2003年，Chen等人［10］对算法进行了改进，改进后的AIEM算法适用于更为广阔的粗糙面参数范围，应用于地形效应［11］特征研究。无论是传统的IEM法还是AIEM法，其高效性主要体现在只考虑粗糙面面元间散射场的一次互耦作用，从而得到散射远场的近似解。实际应用中发现，随着粗糙面粗糙度的增大，粗糙面面元间的多次互耦作用增强，往往不能忽略。

在传统IEM算法的基础上提出迭代IEM法，与传统IEM法不同，该算法考虑了粗糙面面元间的多次互耦。由于使用近场格林函数进行方程求解，散射场不能简化为传统IEM法所使用的积分形式的近似解，但能更为有效地用于计算粗糙面上的散射场，尤其是散射近场。首先介绍迭代IEM法的数学原理，再通过数值实验证明算法的有效性，进一步经过对比说明迭代IEM算法的性能。

1 迭代IEM法的数学模型

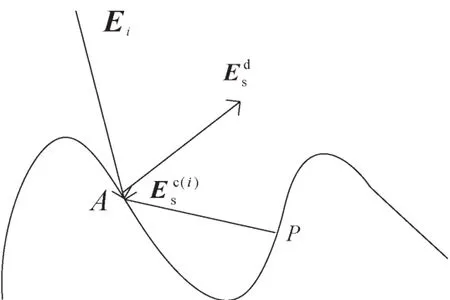
图1 迭代IEM算法模型示意图 Fig.1 Model scheme of iterative IEM

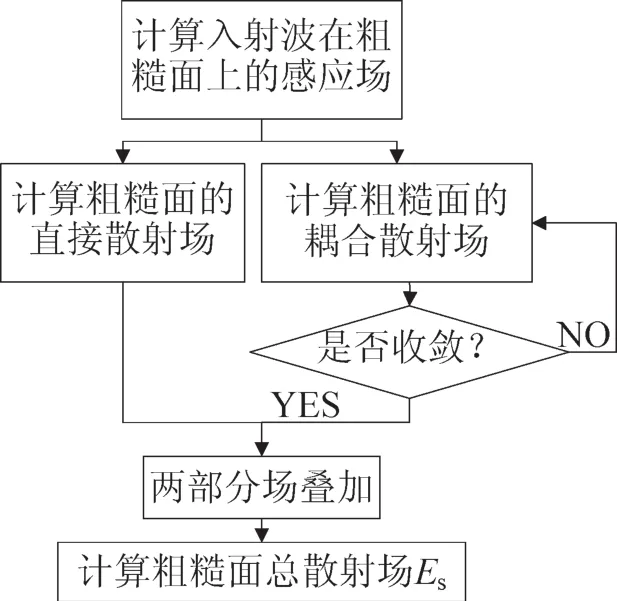
图2 迭代IEM算法流程示意图Fig.2 Flow chart of iterative IEM

2 数值试验与结果

2.1 算法检验

以l=1.0λ，σ=0.0，0.1，0.3，0.5λ（其中，l是相关长度，σ是起伏表面的均方根高度）［7］的随机粗糙面后向双雷达散射截面（RCS）为例，入射波为垂直极化的平面波，其频率f=300 MHz，沿垂直方向入射。图3给出了本文所提的迭代IEM法与MoM的数值结果比较0均方根误差（RSME）分别为1.51，1.40，1.09，1.32 dB，均小于3 dB，计算结果吻合较好。

2.2 算法性能

固定l=2λ不变，以σ=0.0，0.1，0.2，0.4λ的4组金属随机粗糙面为例，这些粗糙面均满足KA算法的有效性条件［12］。假设入射波为VV极化的锥形波（锥形波宽度为3 m），入射方向与上例保持不变，计算距粗糙面上方1 km处的一系列检测点P的散射场值。图4给出了不同粗糙度情况下Ecs（y）的数值对比。图5给出

了

只使用KA法和使用迭代IEM法后的计算结果比较。

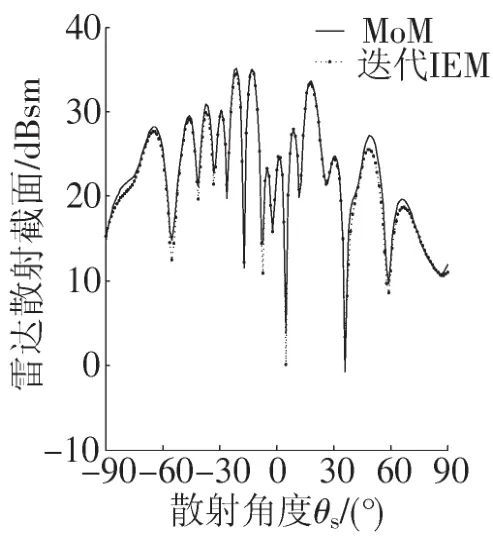
图3MoM与迭代IEM的双站RCS对比结果Fig.3 RCS contrast between MoM and iterative IEM

图4 不同粗糙度的耦合电场场强最值对比Fig.4 Coupling electric field intensities in different surface roughnesses

如图4所示，当粗糙面为δ＜0.1的光滑型大尺度随机粗糙面时，面元间的耦合作用低于0.5 C，此时，迭代IEM法的计算精度与KA法相近（见图5（a～b））。也就是说，在这种粗糙面条件下，迭代IEM法能进一步简化为KA算法。而当δ＞0.2时，粗糙面面元间的耦合作用增强，迭代IEM法和KA法的数值结果表现出明显差别（见图5（c～d）），这时，忽略面元间的耦合作用将导致较大计算误差。

图5 平板上所得的RCS对比图Fig5 RCS comparison between KA and iterative IEM

图6（a）给出了计算以上4组金属随机粗糙面散射场时粗糙面元间的耦合次数对比。图6（b）展示了不同耦合次数下迭代IEM法的计算结果比较。图6的数据显示，尽管粗糙度的增大会导致耦合增强，但对于金属随机粗糙面来说，一般只需考虑5次互耦，其Ecs的数值便可衰减。

表1给出了图3的实例中迭代IEM法与KA法、MoM法的计算性能比较。表中的数据显示，使用迭代IEM法后，计算误差从只使用KA算法的RMSE=2.95 dB减小为1.77 dB，具有更高的计算精度。与MoM法相比，内存需求减少了9倍，计算速度提高了4.5倍以上，就算与使用了多层快速多极子技术（MLFMA）加速后的MoM法相比，计算速度仍然提高了2倍。

表1 迭代IEM与其他算法的计算性能比较Tab.1 Performance comparison between iterative IEM and other methods

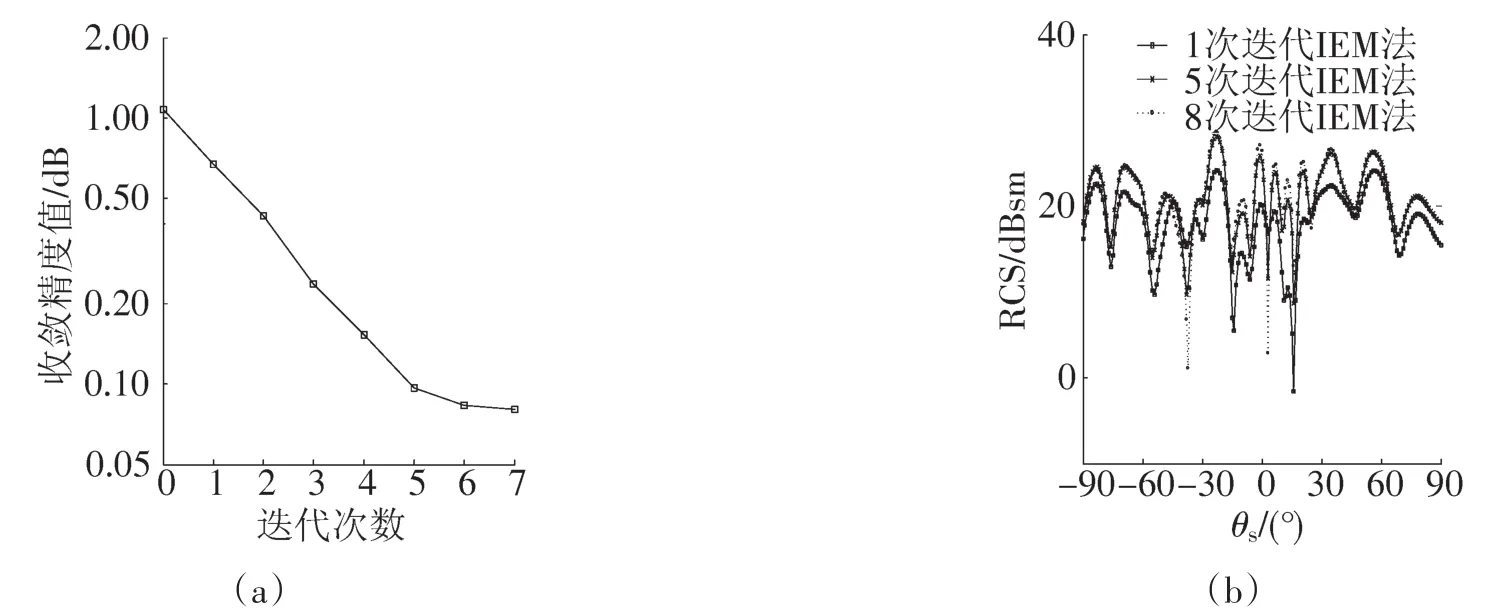
图6 不同迭代次数的IEM法对比结果Fig6 RCS contrast of different IEM iterations

3 结论

由于考虑了粗糙面面元间的耦合场作用，迭代IEM法可用于计算不同尺度条件下的粗糙面的散射场。当粗糙面的粗糙度为δ＜0.1的光滑型大尺度粗糙面时，迭代IEM法的计算精度与KA法相当，这时，算法还可进一步简化为KA法。而当粗糙面粗糙度增大时，迭代IEM法的计算精度表现出优于KA法并更接近MoM法的特点，计算速度与MoM法相比则提高了4.5倍以上，就算与使用了多层快速多极子技术（MLF⁃MA）加速后的MoM法相比，也仍然提高了2倍，并且内存需求量更低，证明了算法具有高效性的特点。

［1］HARRINGTON R F.Field computation by moment methods［M］.New York：Macmillan，1968:1-98.

［2］COLAK D，BURKHOLDER R J，NEWMAN E H.Multiple sweep method of moments analysis of electromagnetic scattering from 3D targets on ocean-like rough surfaces［J］.Microwave and Optical Technology Letters，2007，49（1）：241-247.

［3］金亚秋，刘鹏，叶红霞.随机粗糙面与目标复合散射数值模拟理论和方法［M］.北京：科学出版社，2008：1-3.

［4］THORSOS E I.The validity of the kirchhoff approximation for rough surface scattering using a gaussian roughness spectrum［J］.Acoust SocAm，1988，83（1）：78-92.

［5］刘志伟，张月圆，陈嘉琪.移变模式双站SAR信号模型及电磁仿真研究［J］.华东交通大学学报，2012，29（1）：24-29.

［6］THIELE G A，NEWHOUSE T H.A hybrid technique for combining moment methods with the geometrical theory of diffraction［J］.IEEE TransAntennas Propagat，1975，23：62-69.

［7］叶红霞，金亚秋.三维随机粗糙面上导体目标散射的解析［J］.物理学报，2008，57（2）：839-846.

［8］TSANG L，KONG J A，DING K H.Scattering of electromagnetic waves［M］.New York：Wiley，Theories and Applications，2002：407-416.

［9］ LI Z，FUNG A K.A reformulation of the surface field integral equation［J］.J Electromagnetic Waves and Application，1991，5（2）：195-203.

［10］高婷婷.基于IEM的裸露随机地表土壤水分反演研究［D］.乌鲁木齐：新疆大学，2010.

［11］ CHEN K S，WU T D，TSANG L，et al.The emission of rough surfaces calculated by the integral equation method with a comparison to a three-dimensional moment method simulations［J］.IEEE Trans Geosci Remote Sens，2003，4l：90-101.

［12］李欣欣，张立新，蒋玲梅.被动微波辐射特征地形效应模拟与实验［J］.遥感学报，2011，15（1）：100-109.

［13］闫文哲.电磁场面散射和体散射研究及其应用［D］.杭州：浙江大学，2009：3-8.