PSO优化的LS-SVM在列车弓网系统的建模研究

衷路生，齐叶鹏，杨 辉，龚锦红，张永贤，颜 争

（华东交通大学电气与电子工程学院，江西南昌 330013）

随着铁路的大发展，以前的内燃机车越来越多的被电力机车所取代。电力机车通过受电弓与接触网之间不间断的电气和机械接触获取电能，弓网系统平稳接触受流是电力机车的关键技术之一。弓网系统通过接触网与受电弓之间的接触力耦合在一起，随着列车速度的增加，弓头会在垂向发生振动位移，接触力也会在垂向发生波动，如果波动幅度过大，不仅引起机车受流不良、弓网间磨损磨耗加剧，甚至会导致系统断电、列车停运等重大事故。因此，良好的弓网接触关系是高速列车安全可靠运行的重要条件。

分析弓网接触关系的前提是建立弓网系统的动力学模型。目前，弓网系统的建模问题已经引起广泛关注。文献［1］建立了简单链形悬挂接触网的数学模型并得到垂向振动固有频率和模态振型，分析出接触网的动态响应和受流性能；文献［2］运用机车-轨道耦合动力学理论研究机车-轨道系统对受电弓-接触网系统的振动影响问题；文献［3］首先分别建立接触网模型和受电弓模型，然后通过接触单元得到弓网系统的整体模型，并构建弓网耦合系统的动力学平衡方程，最后采用直接积分法求解建立的平衡方程；文献［4］采用无限长弦模型，将受电弓看作集中质量模型，分析了弓网系统的动态受流性能，研究接触网-受电弓的动态相互作用。此外，还相继提出了弓网系统的吊弦反射模型［5］、集中质量块模型［6］等。已有的弓网系统建模方法虽然能够揭示影响弓网受流质量的某些因素，但已有方法都对弓网的数学模型、边界条件等作出某些假设和简化，难以完全反映弓网系统的真实动力学行为。

基于上述分析，本文提出弓网系统基于粒子群优化（particle swarm optimization，PSO）优化的LS-SVM建模方法。LS-SVM是基于结构风险最小化的SVM的一种扩展，LS-SVM较好地解决了机器学习中遇到的小样本、高维数、非线性、局部极小值、计算量大、运算速度慢等问题，因而，LS-SVM在牵引电机建模［7］、软测量［8］、稀土建模［9］等领域获得了广泛应用。实践表明，LS-SVM的参数（正则化参数γ、核宽度σ）将直接影响其学习精度和泛化能力，目前尚缺乏关于LS-SVM参数的有效计算方法。为此，我们提出基于PSO优化的LS-SVM参数选择方法，避免了LS-SVM参数选择的随机性和盲目性。以弓网子系统模型为基础得到了弓网系统的整体动力学方程。弓网系统接触力的建模和预报实验的结果表明所提出方法的有效性。

1 最小二乘支持向量机理论

以结构风险最小化为基础的SVM方法［10］，通过内积函数定义的非线性变换将输入样本集映射到高维线性特征空间，并在此高维特征空间构造最优分类面。SVM的算法复杂度与训练样本数有关。Suykens等提出的最小二乘支持向量机［11］（LS-SVM）将误差的二范数作为优化的损失函数，用等式约束代替SVM的不等式约束，从而将求解SVM的二次规划问题转化为求解线性方程组的问题。LS-SVM回归问题描述如下：

假设样本数据集为{xk，yk}Nk=1，其中xk∈Rm为m维的输入向量，yk∈R为相应的目标输出，N为样本容量。回归问题首先用非线性映射函数φ（·）把输入空间样本x映射到高维特征空间φ（x），然后在这个高维特征空间构造线性决策函数：

式中：ω是高维特征空间的权向量；b是偏差量。

Suykens等根据结构风险最小化原则，将式（1）的回归问题转化为以下LS-SVM的优化问题：

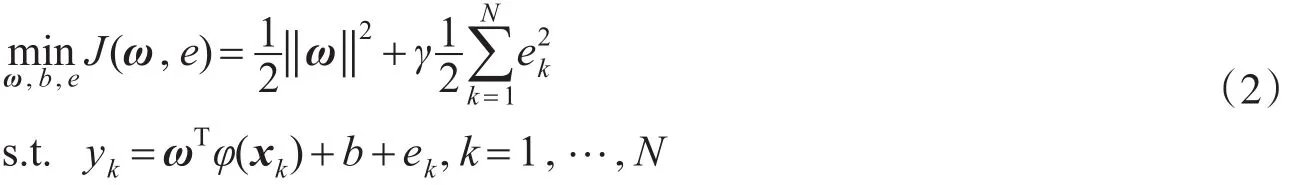
式中：‖ω‖2用以控制模型的复杂度；ek为松弛因子；γ是用于平衡拟合误差和模型复杂度的正则化参数。由于ω的维数高（可能是无限维），直接求解式（2）非常困难，因此将式（2）转化为其对偶问题，并引入La⁃grange乘子进行求解：

其中，αk，k=1，2，…，N是Lagrange乘子。对式（3）应用KKT优化条件得到

消去变量ω和ek，则（4）式可以转化成如下的线性方程组：

其中，K（x，xk）也是对称核函数。常用的核函数有高斯径向基函数、线性函数、多项式函数等。本文选择具有全局收敛性的高斯径向基函数作为核函数，即

其中：σ是核宽度。在选择了核函数之后，则LS-SVM有待于进一步确定的参数有：正则化参数γ和核宽度σ，其中正则化参数γ与LS-SVM的训练误差、泛化能力有关，核宽度σ反映训练样本的分布特性。目前还没有确定γ和σ的统一方法，常用的试凑法计算量大且无法保证获得全局最优解，因此，本文利用PSO算法来优化γ和σ的取值。

2 粒子群算法描述

粒子群优化（panicle swarm optimization，PSO）算法［12］是由Kennedy博士和Eberhart博士在1995 年提出的一种基于群智能进化计算技术。其基本思想是根据个体与群体之间的信息传递及信息共享来寻找最优解。算法初始化为一群随机粒子，然后通过迭代搜索到最优解。在迭代过程中，粒子通过跟踪个体极值Pi和全局极值Pg两个极值来更新粒子自身的速度和在下一轮迭代中的位置。找到这两个极值后，粒子根据它们决定自己的飞行速度和新的位置。

粒子群优化算法根据公式（8）更新粒子速度和位置：

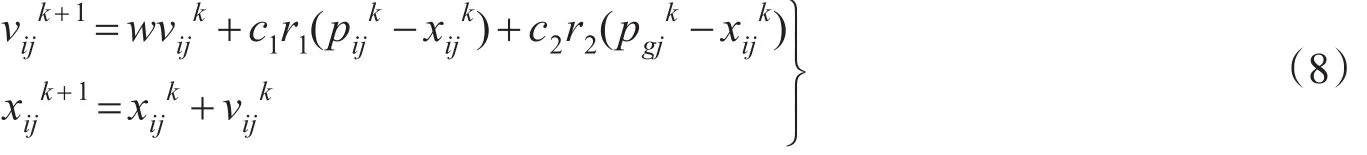
式中：k表示迭代步数；i=1，2，…，M，M是该群体中粒子的总数；j=1，2，…，D，D是优化的参数的总数；，分别表示粒子i在第k步的速度和位置；pijk为第k步粒子i对应于参数j的历史最优解；=为第k步迭代所有粒子对应于参数j的历史最优解；w为惯性权重因子，w取值范围为［0.5，1］；c1和c2是加速度因子，取值范围［1，2］；r1和r2是均匀分布于［0，1］之间的随机数；d表示一个d维的参数空间。在每一次迭代中，每个粒子都由适应度函数来计算适应值，本文采用均方误差函数作为适应度函数，公式为

式中：Fit（i）是第i个粒子的适应值；yij是第i个粒子j个样本的输出值；是j个样本的期望输出值。

在PSO的参数中，w的选择很重要，较大的w有较好的全局搜索能力，而较小的w则有较强的局部搜索能力。所以，w在前期优化过程中应取较大值以获得好的全局搜索能力，后期优化过程中取较小值以得到好的局部搜索能力，w通常根据以下经验公式确定

式中：wmax一般取值0.9～1.4；wmin取0.4；k是当前迭代次数，Kmax是最大迭代次数。

利用粒子群算法优化LS-SVM参数的具体步骤将在第4小节的仿真部分给出。

3 弓网系统建模分析

弓网是通过弓网接触应力耦合在一起的复杂动力学系统，其结构图如图1所示。通常采用子结构方法［6］建立弓网系统模型，即首先建立接触网、受电弓的子系统模型，然后根据弓网子系统模型的相互耦合关系得到弓网系统的整体动力学模型，接下来分别建立弓网子系统模型。

接触网是具有一定抗弯刚度的线索结构，接触网由支柱、绝缘子、承力索、接触线、吊弦、定位器等组成。接触网的刚度不是常数，而在跨内以及跨间变化，因此，通常将弓网接触看作受电弓与变刚度弹簧系统的接触。借鉴文献［6］的基于有限元方法和最小二乘拟合得到的刚度表达式：

式中：k0为平均刚度，N·m-1；μ1，…，μ5为接触网差异系数；v是电力机车速度，km·h-1；L为接触网间跨距，m；S为接触网相邻吊弦间的距离，m；t为列车运行时间，s。此外，f1，…，f4的计算式为

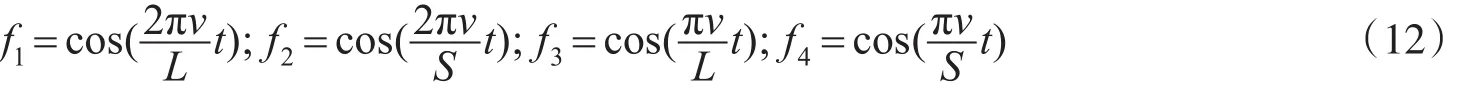
不同悬挂方式（弹性链形悬挂、简单链形悬挂）的接触网对应的式（11）（12）的参数取值也不相同。

受电弓安装在动车顶部，由弓头、滑板、上框架、下框架、上升或下降弹簧及阻尼器组成。一般采用等效质量模型来研究受电弓的动力学行为。根据等效质量模块数目可以分为一元，二元及多元模型。本文采用如图2所示的二元受电弓等效模型，根据图2写出弓网耦合系统动力学方程：

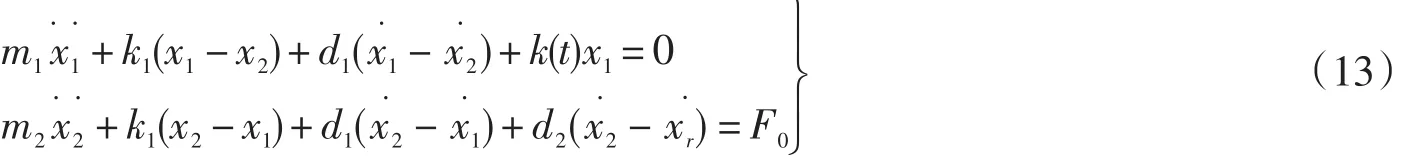
式中：m1,m2分别为弓头和框架等效质量，kg；d1，d2分别为弓头与框架间阻尼和框架与动车车体间的阻尼，N·s·m-1；k1为弓头与框架间刚度，N·m-1；k（t）为接触网等效刚度，N·m-1；F0为静抬升力，N ；xr为来自电力机车的激扰信号。

图1 弓网系统结构图Fig.1 Pantograph-catenary system structure chart

图2 弓网系统二元等效模型Fig.2 Binary equivalent modeling of the pantograph-catenary system

4 基于PSO优化的LS-SVM弓网仿真

基于以上分析，本节应用基于PSO优化的LS-SVM在simulink环境下对弓网系统进行数值仿真，并将本文方法、常规LS-SVM方法以及子空间辨识方法所得的结果进行对比分析。利用Matlab的simulink模块和根据（13）式搭建弓网系统动力学模型，仿真中的弓网模型参数为

k0=3 684.5，μ1=0.466 5，μ2=0.083 2，μ3=0.260 3，μ4=-0.280 1，μ5=-0.336 4，L=63 m ，S=10 m ，m1=6.5 kg ，m2=12 kg ，k1=2650N·m-1，d1=100N·s·m-1，d2=70N·s·m-1，静提升力F0= 90 N ，xr取噪声功率为0.01的白噪声，速度v=200 km·h-1。

运行simulink仿真图，用示波器观测接触力曲线如图3所示，同时保存仿真中获得的数据用于LS-SVM进行建模和预备试验。

为便于分析实验结果，首先给出PSO优化LS-SVM的弓网建模步骤：

Step1：确定PSO的粒子总数M、最大迭代步数Kmax、粒子初始的位置值和速度值、加速度因子、惯性权重因子的最大值wmax和最小值wmin；设定LS-SVMγ和σ的初始值；记迭代步数初始值k=1；

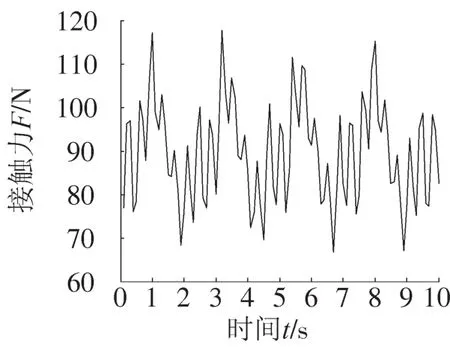
图3 弓网系统接触力仿真曲线Fig.3 Contacting force simulation curve of the pantograph-catenary system

选取图3simulink仿真保存的100组数据，其中前80组作为训练数据，后20组作为检验数据来验证模型的效果。应用上述PSO优化LS-SVM的算法、常规LS-SVM、子空间辨识方法［12-13］分别进行弓网模型的建模与预报试验。PSO和LS-SVM的参数取值为：Kmax=200，M=10，wmax=0.9，wmin=0.4，c1=1.5，c2=1.7,γ和σ的初始值由MATLAB随机函数产生。

LS-SVM的输入是等效质量模块的垂向位移x1和x2与等效质量模块的速度和，输出是弓网间接触力。PSO迭代的适应度曲线如图4所示，参数c1=1.5，c2=1.7，终止代数为200步。经过200次的迭代和PSO优化得到的γ为669.375 3，σ为5.700 1。常规LS-SVM采用的是交叉验证的方法得到的γ=536.270 1，σ=7.768 47。图5是PSO优化LS-SVM的建模误差（式（9））与迭代步数的关系图。由图4可知，PSO优化的建模误差经过2步迭代快速下降到0.0378 2，经过搜索寻优，建模误差在第80步即可达到稳定的最小值，说明PSO优化的γ和σ只需80步迭代就能收敛到全局最优解。

基于以上得到的PSO优化LS-SVM模型、常规LS-SVM模型、子空间模型，应用20组检验数据分别进行弓网系统接触力的预报，3种方法的预报结果如图5所示。从图5可以看出，PSO优化的LS-SVM模型对接触力的预报值几乎与实际的接触力重合，说明LS-SVM模型的预报精度高；子空间模型对接触力的预报值与实际的接触力存在较大偏差，说明子空间模型的预报精度差；常规LS-SVM模型的预报精度介于PSO优化LS-SVM和子空间模型之间。3种模型的具体相对误差见表1。

Step2：以当前的γ和σ训练LS-SVM，根据式（9）计算训练样本的均方误差作为PSO的适应度值；

Step3：由得到适应度值，根据式（10）计算惯性权重因子，依据式（8）更新PSO的位置和速度（即搜索更好的γ和σ），并令k=k+1；

Step4：如果k＜Kmax，返回Step2继续迭代；否则将获得的γ和σ建立LS-SVM的回归模型；

Step5：利用LS-SVM回归模型对验证数据进行预报。

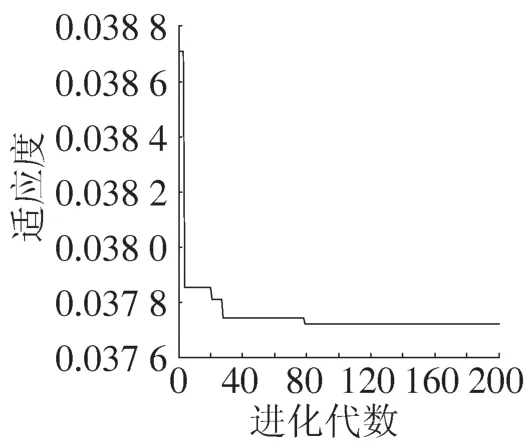
图4 PSO迭代的适应度曲线 Fig.4 Fitness curve of PSO iteration

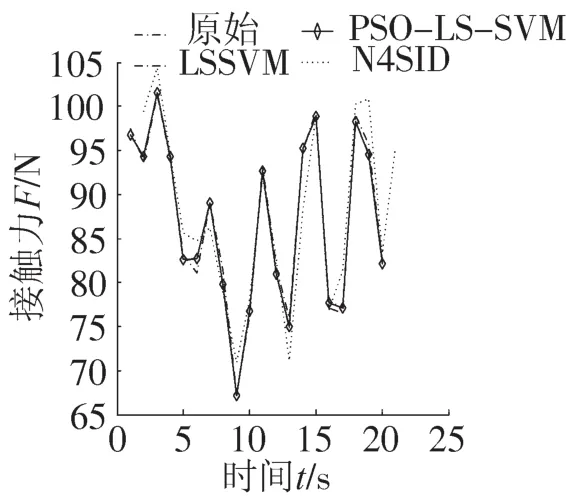
图5 接触力曲线拟合比较图Fig.5 Fitting contrast of contacting force curve

表1 拟合曲线误差对比Tab.1 Error contrast of fitting curve

5 结论

提出PSO优化LS-SVM的列车弓网系统建模方法。利用具有全局搜索特性的PSO算法来优化LS-SVM的正则化参数γ与核宽度σ，克服了LS-SVM参数选择的盲目性。采用子结构方法分别建立列车接触网、受电弓子系统模型，进而得到弓网系统的整体耦合模型。最后基于matlab平台进行弓网系统接触力的建模和预报实验，仿真结果表明，PSO优化LS-SVM模型相比于常规LS-SVM模型、子空间辨识模型具有更高的接触力预报精度，PSO优化LS-SVM模型能够反映弓网系统的实际运行状况，本文PSO优化LS-SVM在弓网系统的应用尝试为具有综合复杂性的弓网系统的建模和控制提供了新的方法。

［1］张卫华，沈志云.接触网动态研究［J］.铁道学报，1991，13（4）：26-33.

［2］翟婉明，蔡成标.机车-轨道振动对受电弓-接触网系统动力学的影响［J］.铁道学报，1998，20（1）：32-38.

［3］周宁，张卫华.基于直接积分法的弓网耦合系统动态性能仿真分析［J］.中国铁道科学，2008，29（6）：71-76.

［4］吴燕，吴俊勇，郑积浩，等.高速受电弓-接触网动态受流性能及双弓距离的研究［J］.铁道学报，2010，32（4）：38-43.

［5］ BAUER K H，BUCKSCH R，LEMER F，et al.Dynamische krite2rien die auslegung von fahrleitungen［J］.ZEV Glasers Annalen，1979，103（10）：365-370.

［6］杨岗，李芾.高速动车受电弓滚动弓头特性研究［J］.机车电传动，2010（4）：79-83.

［7］李娜，杨恒，屈志坚，等.基于改进最小二乘支持向量机的电力机车牵引电机建模［J］.铁道学报，2011，33（3）：23-27.

［8］陈帅，朱建宁，潘俊，等.最小二乘支持向量机的参数优化及其应用［J］.华东理工大学学报：自然科学版，2008，34（2）：278-282.

［9］陆荣秀.混合核函数支持向量机在系统建模中的应用［J］.华东交通大学学报，2010，27（2）：63-67.

［10］VAPNIK V N.The nature of statistical learning theory［M］.New York：Springer，1995：120-125.

［11］ SUYKENS J A K，VANDEWALLE J.Least squares support vector machines［J］.Neural Processing Letter，1999，9（3）：293-300.

［12］衷路生，杨辉.基于辅助变量的闭环系统子空间辨识［J］，控制与决策，2009，24（5）：670-674.

［13］甘岚，吕文雅.基于LLE和LS_SVM的胃粘膜肿瘤细胞图像分类［J］.华东交通大学学报，2011，28（3）：83-87.

［14］张曙光，金学松.高速轮轨系统动力学研究体系及其系统建模［J］.科学通报，2007，52（7）：855-860.