基于层次分析法的黄土滑塌风险评价指标权重分析
唐亚明,程秀娟,薛 强,毕俊擘
(中国地质调查局西安地质调查中心,陕西西安 710054)
0 引言
评价指标的权重直接影响到评价结果的准确性和客观性,权重的分析有定性判断和定量计算两种途径。在滑坡评价指标权重分析中各种方法均有采用,如德尔菲法[1]、熵值法[2]、梯形模糊数加权法[3]、层次分析法[4-8]等,尤以层次分析法应用较为广泛[9-10]。美国著名运筹学家T.L.Saaty于20世纪70年代提出的层次分析法(AHP)把复杂问题按照主次或支配关系分组而形成有序的递阶层次结构,利用数学方法确定每一层中所有元素的相对重要性权值,最后通过排序结果来确定最终权重,具有有效结合定性判断和定量计算的优点[11]。
本文即采用层次分析法的基本原理和算法,在先前研究确定的黄土滑塌灾害风险评价指标体系[12-13]的基础上,建立危险性递阶层次模型和危害性递阶层次模型,通过两两比较矩阵计算各分层指标权重,再通过合成权重计算得到各指标的最终权重,并在各次权重计算时都进行一致性检验,最后将计算所得的指标权重应用于一个斜坡实例,进行危险性、危害性和风险的半定量评价。
1 层次结构模型的建立
1.1 评价指标的确定
滑坡的风险一般用危险性×危害后果确定,因此如果分别得到了危险性指标和危害后果指标,则风险大小即可确定[1]。危险性应考虑以下三方面情况:过去容易失稳的地方现在仍旧容易失稳(工程地质类比法);斜坡本身因素,如地貌、地形、斜坡结构等所决定的失稳趋势大小;触发因素对斜坡稳定性的影响。基于此考虑,危险性指标的选取如下:(1)物质成分:典型的砂黄土最有利于这种“黄土滑塌”的产生,体现出运动速度较快的“垮塌”特点,滑动面也不明显。随着粘粒含量增多,逐渐呈现出典型滑坡的滑体、滑带、滑床的特点。因此,粘粒含量的多少是这类滑坡的重要控制因素之一。(2)失稳证据:主要看历史上是否容易发生滑坡,以及现今变形的迹象。(3)地貌形态:根据统计规律,黄土滑坡或崩塌发生在幼年期沟谷中的概率比壮年期、老年期的要大,黄土梁正处于沟谷地貌的侵蚀强烈期,较之黄土峁和黄土塬具有更大的斜坡失稳概率,因此沟谷地貌和沟间地貌的发育阶段可作为评价指标;另外,在黄土斜坡上还广泛发育着各类黄土洞穴,它们的规模和发育阶段对斜坡稳定性影响也很大。(4)斜坡形态:根据这一地区的统计规律,坡度、坡型、坡高等斜坡形态是斜坡失稳的直接控制性因素,因此作为重要的评价指标。(5)结构特征:不同的地层结构,如黄土+基岩或黄土+古土壤对稳定性影响较大,此外,不同的土岩接触面产状和土体结构本身对坡体稳定性影响也很大,均作为评价指标。(6)水的作用:主要有地表水作用(侧蚀强烈程度),地下水赋存状态,地下水活动强度(泉流量大小)等评价指标。(7)触发因素:该地区黄土滑坡的触发因素主要有三种,分别是地震、降雨和人类活动,由于地震和降雨属于区域性的统一影响因素,不宜作为评分指标,而人类活动在不同的斜坡单元具有很大的差异性,可作为重要的评分指标,人类活动对斜坡稳定性的影响分为正负两方面,如开挖、灌溉等属于负面影响,而排水、削坡、支挡等属于正面影响。(8)滑塌强度:是对尚未发生的、潜在的地质现象(在此指黄土滑塌)进行评价,是在调查现有地质条件的基础上,预测潜在滑塌体的体积大小、运动速度、滑塌路径、可能影响的范围等,从而判断其强度大小。
危害后果主要由可能的承灾体的数量和易损性决定,将承灾体分为固定人口、交通人口、建筑财产、基础设施财产、其他财产5类,每类根据不同的数量级别赋予不同的分值。易损性是指在一个地区内一个或一组给定的承灾体受滑坡影响的损失程度,以0(无损失)到1(全部损失)表示,按承灾体的类别可分为财产易损性和人员易损性。财产易损性根据建筑物、基础设施的材料、结构、使用年限等,评价在相同的滑坡强度冲击下,其抵抗破坏的能力。人员易损性与滑塌的体积和速度、人员与滑塌的相对位置、是否受到防护、是否有预警信号、人的受教育程度、身体强壮程度等均有关系。
因为危险性和危害性属于两个不同的评价对象,且风险是两者相乘的结果,故对危险性和危害性分别构建层次分析模型。
1.2 危险性层次分析模型
黄土滑塌所发育的地质环境条件具有共性,而其个体因素,如斜坡坡度、坡高、裂缝陷穴、地下水等则有较大的差异,具体的评价指标参见文献[12-13]。根据具体的评价指标分析,分为3个层次是比较恰当的,能够较清晰地反映不同因素和准则之间的逻辑关系,既可避免层次过少无法体现个体差异,又可避免层次过多给实际评判带来不便。第一层是总目标危险性大小,设为A,权重为1.0;第二层包括物质成分、失稳证据、微地貌、斜坡形态等8项,指标设为Bi(i=1、2、…8),其相对于第一层的权重设为;第三层又细分为历史数据、现今变形等22个指标,设为Ci(i=1、2、…22),其相对于第二层的权重设为(图1)。
1.3 危害性层次分析模型
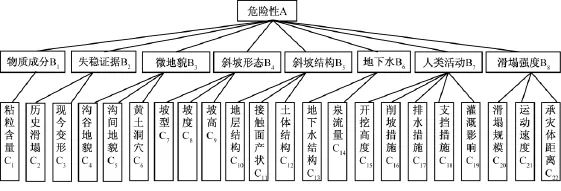
图1 黄土滑塌危险性递阶层次模型Fig.1 The hierarchy structural model for the loess collapse hazards analysis
危害性的递阶层次结构也分为3层(图2)。第一层是总准则危害性大小,设为D,权重为1.0;第二层包括承灾体的大类别,含固定人口、交通人口、建筑、基础设施、其他财产5大类,另外易损性也是评价滑塌危害性大小的重要方面,因此第二层指标共有6项,设为 Ei(i=1、2、…6),其权重设为;第三层将承灾体的大类又分为若干小类(住宅人口、办公生产人口等),并将易损性分为人员易损性和财产易损性,共有15个指标,设为 Fi(i=1、2、…15),权重设为,各层次结构和指标构成见图2。
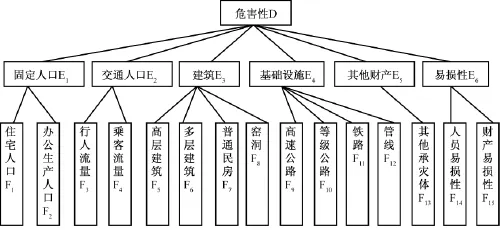
图2 黄土滑塌危害性递阶层次模型Fig.2 The hierarchy structural model for the loess collapse consequence analysis
2 权重的计算
层次分析法的基本原理可概括为:(1)分析系统中各因素之间的关系,建立系统的递阶层次结构;(2)对同一层次的各元素关于上一层次中某一准则的重要性进行两两比较,构造两两比较的判断矩阵;(3)由判断矩阵计算被比较元素对于该准则的相对权重,并进行一致性检验;(4)计算各层元素对系统目标的合成权重[11,14]。
以 A 表示准则,Bi、Bj(i,j=1,2,…,n)表示因素,Bij表示Bi对Bj的相对重要性,则由Bij可组成一个两两判断矩阵P=(Bij)n×n(Bij的取值及含义如表1)。对矩阵的每一行向量求几何均值并归一化,所得特征向量Wi即为各指标权重。

表1 两两比较矩阵Bij的取值及含义Table 1 The value and its meaning of Bijin comparative matrix
2.1 分层权重计算
(1)危险性权重计算
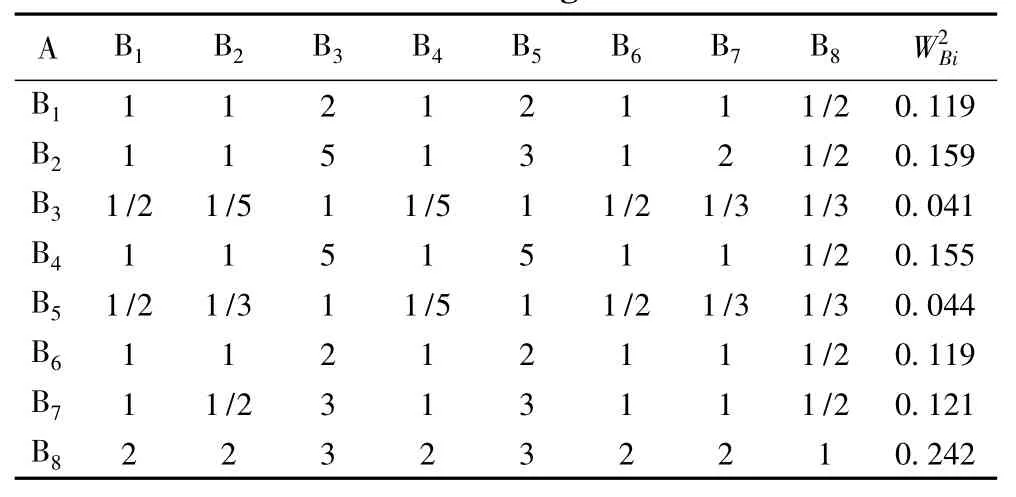
表2 判断矩阵 P1(A→B1-8)及权重值Table 2 The comparative matrix P1(A→B1-8)and factors weights

表3 判断矩阵 P2(B2→C2-3)及权重值Table 3 The comparative matrix P2(B2→C2-3)andfactors weights

表4 判断矩阵 P3(B3→C4-6)及权重值Table 4 The comparative matrix P3(B3→C4-6)and factors weights
权重分析是由上而下进行的。先对第二层的8个指标之间进行两两比较,确定它们对于总准则A危险性的相对重要性,构造第一个判断矩阵P1(表2),通过方根法求解特征向量,得0.159、0.041、0.155、0.044、0.119、0.121、0.242),即为物质成分B1、失稳证据B2、微地貌B3、…滑塌强度B8等的权重系数。接下来分别构造第三层指标相对于第二层各准则的两两比较判断矩阵。物质成分准则下只有粘粒含量1个指标,因此其权重其余的分别构造判断矩阵,历史滑塌C2、现今变形C3对于失稳证据B2可构造判断矩阵P2(表3);沟谷地貌C4、沟间地貌C5、黄土洞穴C6对于地貌形态B3可构造判断矩阵P3(表4)等等,通过同样的几何均值归一化方法可得到一系列的权重系数
以上权重系数(特征向量)是否合理,还需要对判断矩阵Pi进行一致性检验。一致性指标的计算公式为:
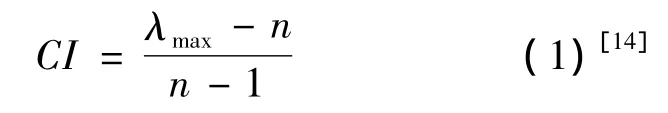
式中:λmax为矩阵的最大特征根,计算公式为:
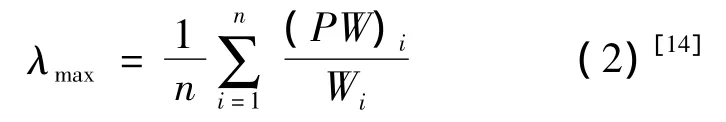
检验时使用一致性比例进行判定,其公式为:

式中:RI——1~9阶矩阵的平均随机一致性指标(可查表得),若CR<0.1,认为判断矩阵的一致性是可以接受的,若CR>0.1,则应对矩阵做适当修正[14]。
下面以P3为例说明检验过程。首先计算排序向量:

再将表4中的数据代入式(2)得最大特征根(λmax=3.04,根据式(1)得一致性指标 CI=0.02,查表知3阶矩阵的平均随机一致性指标RI=0.58,则一致性比例CR=0.03<0.1,一致性良好,检验通过。
对所有矩阵均做一致性检验,结果显示其一致性比例CR值在0~0.03,均远小于0.1,说明构造的两两判断矩阵一致性良好。
(2)危害性权重计算
用同样的方法计算危害性指标的权重,可分别得到第二层指标权重和第三层指标权重的值,一致性检验比例CR在0~0.05,均小于0.1,检验通过。
2.2 合成权重计算
以上得到的仅是一组元素对上一层中某元素的权重向量,要得到最低层中各因素对于总目标的排序权重,要进行“合成权重”的计算。假定已算出第k-1层上 nk-1个元素相对于总目标的权重向量为W(k-1),第k层上nk个元素对k-1层上第j个元素为准则的权重向量为,其中不受j支配的元素权重为零。令P(k)为nk×nk-1矩阵,那么第k层上元素对总目标的合成权重向量计算公式为:
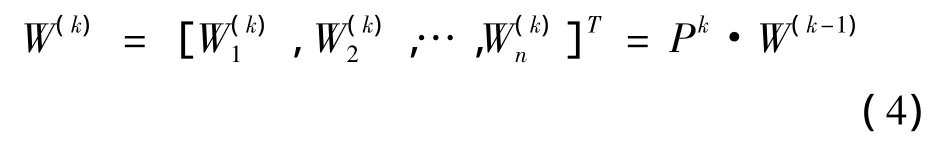

表5 合成权重计算表Table 5 The calculating table of integrated weights
危险性指标的合成权重根据式(4)计算,各指标相对于总目标的权重,计算过程及结果见表5,WA即为各评价指标的最终权重。对合成权重同样进行一致性检验,其一致性指标CI=0.009,平均随机一致性指标RI=0.415,一致性比例CR=0.021<0.1,检验通过。
用同样的方法计算危害性指标的合成权重,WD,可得各指标相对于危害性总目标的最终权重(计算表略)。其一致性检验结果,CI=0.003,RI=0.115,CR=0.023 <0.1,检验通过。
3 应用实例
上述建立的评价指标和权重体系比较适用对多个斜坡单元的风险大小对比,因为使用统一的评价指标体系和权重大小,最后的得分反映了在相同评判标准下每个斜坡单元发生滑塌灾害的风险大小,这对于排定防治优先次序和土地利用规划等具有指导意义,本文的出发点正基于此。但为了说明具体的评价过程,下面以一个单体斜坡单元作为评价对象,将上述研究成果加以应用。
3.1 斜坡概况
选取的评价单元位于陕西省延安市大石佛沟村西一处典型的黄土斜坡上(图3),斜坡面积172.6×103m2,坡度平均40°,坡高120m,属于侵蚀型黄土梁地貌,黄土覆于下伏基岩古地形之上。地层为中、晚更新世黄土,厚度10~30m不等,内含古土壤层,基岩为中厚层状侏罗系延安组砂岩,近水平状出露于坡脚,未见地下水。坡体上变形迹象不明显,发育有生物洞穴。坡体下部斩坡建房,有简单的削坡措施,坡比>2,但无防水及支挡措施。承灾体主要为居住在2层简易砖房内的农户,约10户50人,房前有村道1条位于承灾体范围内,行人和车流量很少。

图3 斜坡评价单元(图中白线为单元边界)Fig.3 Slope unit for assessment(in picture the blue line is unit boundary)
3.2 斜坡风险评价
分别对危险性和危害性的第三层评价指标Ci及Fi进行分档,按照对危险性或危害性作用的大小每个指标划分为4档,如“现今变形”指标划分为迹象明显、迹象较明显、迹象不明显、无迹象4个档次,“坡度”划分为 θ≥60°、60°> θ≥45°、45°> θ≥30°、θ<30°四个档次。每档给定一个分值,分别是1分、4分、7分、10分,调查时依据斜坡的实际情况,确定档次和相应的分数,用分数乘以权重则可得到该指标的分值(表6)。
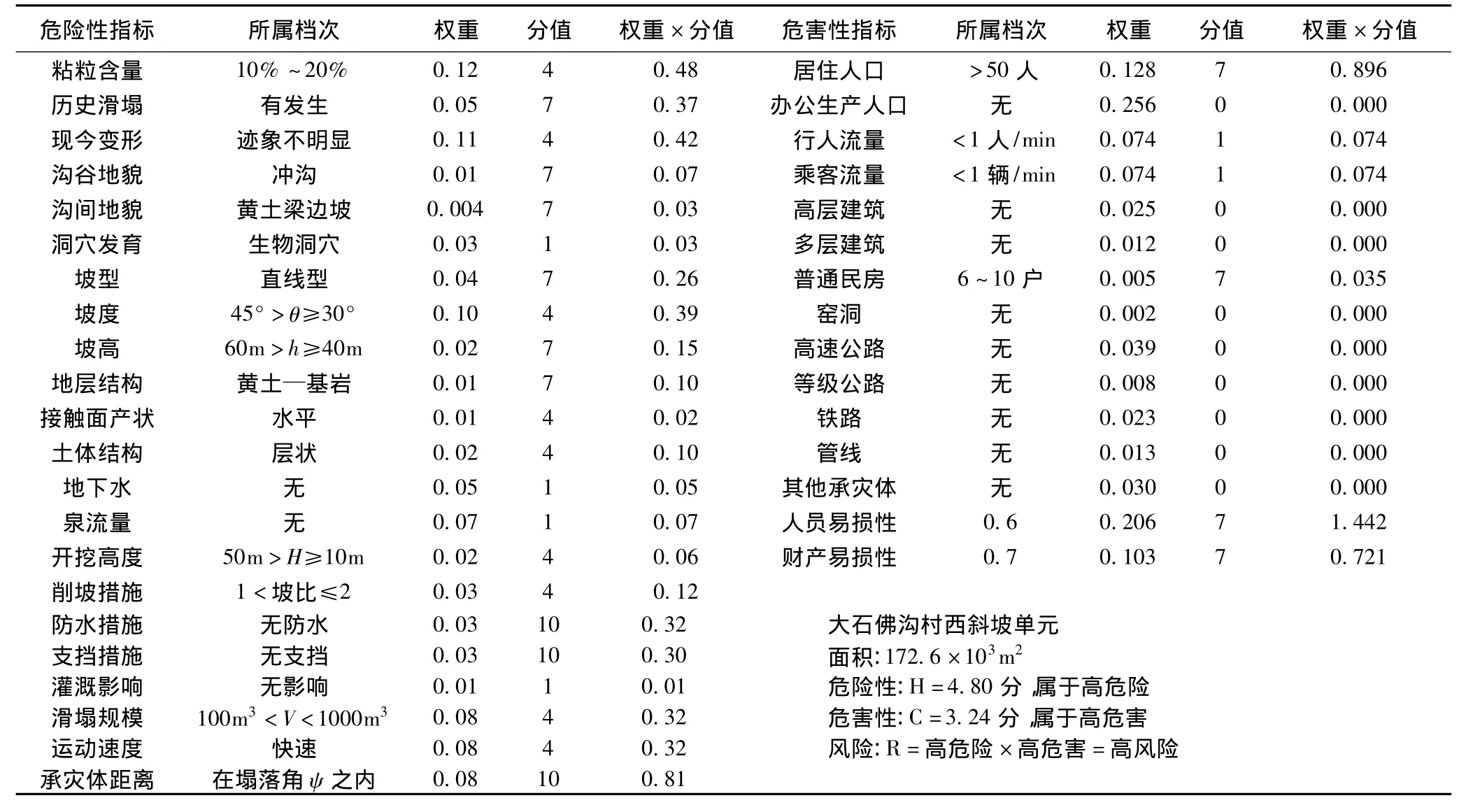
表6 斜坡单元的黄土滑塌危险性、危害性、风险评价表Table 6 Loess collapse hazards,consequence and risk assessing table of one slope unit
4 结论
(1)根据层次分析法计算结果,黄土滑塌危险性的22个指标(粘粒含量、历史滑塌、现今变形、沟谷地貌、沟间地貌、黄土洞穴、坡型、坡度、坡高、地层结构、接触面产状、土体结构、地下水结构、泉流量、开挖高度、削坡措施、防水措施、支挡措施、灌溉影响、滑塌规模、运动速度、承灾体距离)的权重 WA=(0.12、0.05、0.11、0.01、0.004、0.03、0.04、0.10、0.02、0.01、0.01、0.02、0.05、0.07、0.02、0.03、0.03、0.03、0.01、0.08、0.08、0.08)。
(2)黄土滑塌危害性的15个指标(住宅人口、办公生产人口、行人流量、乘客流量、高层建筑、多层建筑、普通民房、窑洞、高速公路、等级公路、铁路、管线、其他承灾体、人员易损性、财产易损性)的权重WD=(0.128,0.256,0.074,0.074,0.025,0.012,0.005,0.002,0.039,0.008,0.023,0.013,0.030,0.206,0.103)。
(3)根据上述指标和权重,对陕西省延安市大石佛沟村西一处典型黄土斜坡单元进行了评价,其发生滑塌的危险性得分为4.80分,为高危险,危害性得分为3.24分,为高危害,最后的风险评价结果为高风险。
[1]夏元友,朱瑞赓.斜坡稳定性综合评价方法的集成式因素权重赋值方法[J].中国有色金属学报,1998,8(1):165-169.XIA Yuanyou,ZHU Ruigeng.An integrated index-weight determination method for comprehensive evaluation on slope stability[J].The Chinese Journal of Nonferrous Metals,1998,8(1):165-169.
[2]张晨,王清,陈剑平.金沙江流域泥石流的组合赋权法危险度评价[J].岩土力学,2011,32(3):831-836.ZHANG Chen,WANG Qing,CHEN Jianping.Evaluation of debris flow risk in Jinsha river based on combined weight process[J].Rock and Soil Mechanics,2011,32(3):831-836.
[3]解传银.基于权重模型的滑坡灾害敏感性评价[J].中南大学学报(自然科学版),2011,42(6):1772-1779.XIE Chuanyin.Landslides hazard susceptibility evaluation based on weighting model[J].Journal of Central South University(Science and Technology),2011,42(6):1772-1779.
[4]樊晓一,乔建平,陈永波.层次分析法在典型滑坡危险度评价中的应用[J].自然灾害学报,2004,13(1):72-76.FAN Xiaoyi, QIAO Jianping, CHEN Yongbo.Application of analytic hierarchy process in assessment of typical landslide danger degree[J].Journal of Nature Disasters,2004,13(1):72-76.
[5]姚玉增,任群智,李仁峰,等.层次分析法在山地地质灾害危险性评价中的应用—以辽宁凌源地区为例[J].水文地质工程地质,2010,37(2):130-138.YAO Yuzeng,REN Qunzhi,LI Renfeng,et al.Application of analytic hierarchy process to the probability assessment of mountain geological disasters:a case study of Lingyuan region, Liaoning province [J]. Hydrogeology &Engineering Geology,2010,37(2):130-138.
[6]张卫中,陈从新,张敬东.改进的AHP及其在地灾易发程度分区中的实践[J].土木建筑与环境工程,2009,31(2):85-89.ZHANG Weizhong,CHEN Congxin,ZHANG Jingdong.Improved AHP assessment model and its practice in geological hazard susceptibility zoning[J].Journal of Civil Architectural& Environmental Engineering,2009,31(2):85-89.
[7]赵成,张永军,赵玉红.层次分析法在甘肃省地质灾害易发性评价中的应用[J].冰川冻土,2009,31(1):182-188.ZHAO Cheng, ZHANG Yongjun, ZHAO Yuhong.Application of the hierarchical analytical methods to evaluating geological hazard tendency in Gansu province[J].Journal of Glaciology and Geocryology,2009,31(1):182-188.
[8]王哲,易发成.基于层次分析法的绵阳市地质灾害易发性评价[J].水文地质与工程地质,2007(3):93-98.WANG Zhe,YI Facheng.Evaluation of geological hazard probability of occurrence based on analytical hierarchy process in mianyang city[J]. Hydrogeology &Engineering Geology,2007(3):93-98.
[9]H Yoshimatsu,S Abe.A review of landslide hazards in Japan and assessment of their susceptibility using an analytical hierarchicprocess(AHP)method[J].Landslides,2006(3):149-158.
[10]Sule Tudes,Nazan Duygu Yigiter.Preparation of land use planning model using GIS based on AHP:case study Adana-Turkey[J].Bulletin of Engineering Geology and the Environment,2010,69(2):235-245.
[11]张征.环境评价学[M].北京:高等教育出版社,2004.ZHANG Zheng.Environment assessment theory[M].Beijing:Higher Education Press,2004.
[12]唐亚明,薛强,毕俊擘,等.陕北黄土滑塌灾害风险评价指标体系构建[J].地质通报,2012,31(6):880-890.TANG Yaming, XUE Qiang, BI Junbo,et al.The construction of factors for assessing the risk of collapse at loess slopes in north of Shannxi province[J].Geological Bulletin of China,2012,31(6):880-890.
[13]唐亚明,薛强,李清,等.黄土滑塌灾害风险分级系统研究[J]. 工程地质学报,2012,20(3):45-51.TANG Yaming,XUE Qiang,LI Qing,et al.Slope classifying system study for loess collapse assessment[J].Journal of Engineering Geology,2012,20(3):45-51.
[14]许树柏.实用决策方法—层次分析法原理[M].天津:天津大学出版社,1988.XU Shubai. The utility decision method,analytic hierarchy process[M].Tianjing:Tianjing University Press,1988.

