统一强度理论下桩基极限承载力讨论

谢新斌 冯小平 周显川

1新疆地矿局第十地质大队（848000） 2新疆地矿局第十地质大队（848000）

0 引言

朗肯，太沙基，迈耶霍夫[1]等经典地基极限承载力公式是基于Mohr-Coulomb准则推导。但Mohr-Coulomb准则未考虑中间主应力的影响。由Mohr-Coulomb强度准则推导的地基极限承载力并不能完全反映地基实际情况，推导结果偏于保守，不能充分发挥土体的强度潜能。周小平[2～4]基于统一强度理论的太沙基地基极限承载力，利用统一强度理论求解条形地基极限承载力和考虑中间主应力的太沙基地基极限承载力公式均表明当考虑中间主应力影响时地基极限承载力会提高。

1 统一强度理论

统一强度理论可以表示为[5]:

2 基本假设

1）当地基发生整体剪切破坏，发生如图1所示的太沙基深基础破坏模式[6]。基底平面以下形成连续的滑动面，如取一剖面描述则其滑动面一直延伸到基底面并交于d点，滑动面由直线ab、对数螺旋曲线bc和直线cd三部分组成。

2）基底以下有一部分土体将随基础一起移动而始终处于弹性状态,该部分土体为弹性圆锥体。弹性圆锥体的母线ab为滑动边界的一部分，ab线与水平面成ψ角，并且假设作用在弹性圆锥体侧面上的被动土压力和粘聚力在母线方向的合力为作用在圆锥体侧面的的圆形分布的线荷载。

3）除弹性圆锥体外，在滑动区域范围内的所有土体处于塑性状态，滑动区由径向剪切区Ⅱ和朗肯被动区Ⅲ组成,径向剪切区的边界bc由对数螺旋曲线表示:

式中:φuni为统一强度理论的内摩擦角，r0为起始矢径，θ为任意矢径与起始矢径r0的夹角。朗肯被动区Ⅲ的边界cd为直线与水平面成45°-φuni/2角。

4）基底平面ad环形区域下的土直接受到基础下的土所给予的侧向挤压，使这块土有向上移动并驱使环形面积ad以上的土体也产生了向上的相对移动，从而在环形面积以上土体的边界de和基墩侧面与土之间分别产生了向下的剪阻力τ和摩阻力fs。

3 桩基极限承载力的确定

首先计算基底以上ad环形区域的受力状态，基础侧面上的法向应力σα按静止压力分布，若桩基础侧面与土之间的摩擦角为δ，则作用于基础侧面上的平均法向应力σα和τα为:

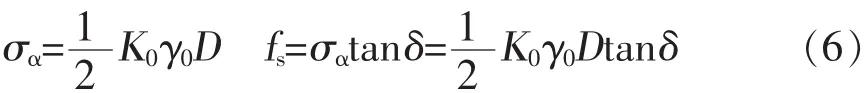
式中:K0为土的静止侧压力系数，γ0为基础底面以上土的容重，D为桩基的埋置深度。

环形区域的外环破坏面土的平均剪阻力假定为:

根据上述基本假定由图2中的圆锥形弹性体的平衡条件可得整体剪切破坏时的极限荷载。

若基础完全粗糙,此时弹性圆锥体ab与基底水平面的夹角，则式（17）可以写成如下形式:

将式（16）代入式（13），则基底完全光滑的承载力系数 Nc，Nq，Nγ可确定。

4 计算算例及结论对比分析

有一直径400mm的圆形桩基础,打入均质黏性土6m，黏性土容重为20 kN/m3，固结不排水抗剪强度指标C0=20 kPa，φ0=30°。设土的静止侧压力系数0.45，桩基与土之间的内摩擦角为δ=12°。下边分别利用文中公式和太沙基公式求桩基极限承载力并加以比较（仅计算）。

基底完全粗糙的情况:

表1 基底完全粗糙时不同b值桩基地基承载力计算结果

应用Matlab软件做出基底完全粗糙时qu随b值的变化曲线见图5。

基底完全光滑的情况:

1）利用太沙基公式

基底完全粗糙太沙基极限承载力:

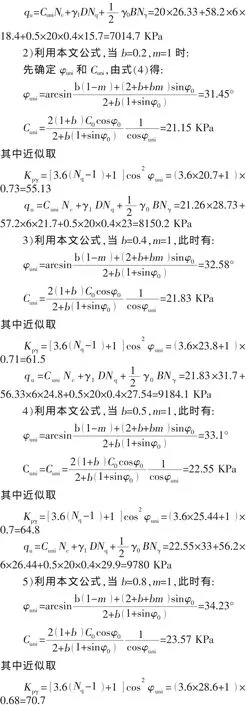
表2 基底完全粗糙时不同b值桩基地基承载力计算结果

应用Matlab软件做出基底完全光滑时qu随b值的变化曲线见图6。

5 结论

1）基于Mohr-Coulomb准则的太沙基桩基极限承载力，由于没有考虑中间主应力的影响，其结果最小，由算例知在基底完全粗糙和完全光滑的条件下由统一强度理论计算的结果随b的增大而增大，当b=0时即为Mohr-Coulomb准则,当b=1时即为双剪强度理论。

2）在实际工程中基底既不是完全粗糙也不是完全光滑的，即ψ角是介于φ和φ/2+45°之间的，但根据两种极端情况下得出的结果，不难得出实际工程中桩基极限承载力亦随b的增大而增大。

3）利用统一强度理论建立了桩基极限承载力的统一解形式，利用此解可以合理的得出不同b值对应的相应解,可以充分发挥材料自身的承载能力，对实际工程有重要意义。

[1]雍景荣,朱凡,胡岱文.土力学与基础工程[M].成都:成都科技大学出版社,1995.

[2]周小平,张永兴.基于统一强度理论的太沙基地基极限承载力[J].重庆大学学报(自然科学版),2004,27(9):133～136.

[3]周小平,张永兴.利用统一强度理论求解条形地基极限承载力[J].重庆大学学报(自然科学版),2003,26(11):109～112.

[4]周小平,黄煜镔,丁志诚.考虑中间主应力的太沙基地基极限承载力公式[J].岩石力学与工程学报,2002,21(10):1554～1556.

[5]俞茂宏.双剪理论及其应用[M].北京:科学出版社,1998.

[6]俞茂宏,杨松岩,刘春阳,刘剑宇.统一平面应变滑移线场理论[J].土木工程学报,1997,30(2):14～26.

[7]钱家欢,殷宗泽.土工原理及计算(第二版)[M].北京:中国水利水电出版社,1996.