不同控制策略下含直驱机组风电场的系统电压稳定研究

赵海岭，王维庆，姚秀萍，常喜强

(1.新疆电力公司昌吉电业局，新疆 昌吉 831100;2.新疆大学电气工程学院，新疆 乌鲁木齐 830047;3.新疆电力调度通信中心，新疆 乌鲁木齐 830002)

0 引言

风力发电是目前技术最成熟、最具开发规模和商业化发展的可再生能源利用形式［1］。大规模地开发和利用风能成为世界新能源领域的一大重要研究课题。然而在电网接纳不断增加的风电穿透功率时，致使风电并网的电压稳定问题逐渐凸显。

变速永磁直驱风电机中全功率变频器的采用，使得该风机有功与无功可控，拥有多种灵活控制策略［2］，具有的优势越来越凸出，在实际风电场中占据比例越来越高，大规模基于直驱风电机组并网风电场越来越多，在基于直驱机组风电场与电网弱联系时，其对电力系统电压稳定影响值得研究。

电压失稳的根源在于线路输送功率与负荷所需的功率无法平衡，最终导致电压崩溃［3］。文献［4－6］对风电场接入电力系统的稳态进行了仿真，其中文献［5］主要是分析风电场的输出功率随风速间歇性和波动性变化对所接入地区电网电压的影响。风电场接入对于含风电场的电网电压稳定、风电注入功率不定与其本身无功特性使得与传统电压稳定问题有着机理上［7－9］的一致。国内外进行了大量细致的研究。文献［10］分析了随风电场容量的不断增加对地区电网电压稳定的不利影响，若系统不能提供足够的无功支持，将会导致地区电网电压瓦解，采用连续潮流计算得出P－V曲线，对地区电网关键母线电压与风场不同出力水平的关系进行了详尽分析，并对某些节点加与不加无功补偿装置对节点电压的影响进行了仿真。文献［11－13］通过得出风场的不同出力下系统相关节点电压，采用描点法绘制P－V曲线，详细研究了含风电系统的电压稳定问题。

针对永磁直驱风力发电技术不同控制策略进行研究，首先建立了永磁直驱同步风力发电机的数学模型，并对其构成的风电场进行等值，通过连续潮流计算，绘制风电场公共接入点(point of common coupling，PCC)、电网重要节点的PV及VQ曲线，针对直驱机组变频器的完善的控制技术，对不同控制策略下含直驱机组风电场的电网静态电压稳定性进行了深入研究。

1 风电电网静态电压稳定机理分析

风电系统静态电压稳定分析的机理是采用连续潮流计算的方法［14］，研究并网风电场在小扰动情况下的风电电网电压稳定问题。其实质是风电机组的有功和无功功率特性、电网坚强程度、电网或风电机组本身是否能够在风电机组连续运行中提供足够的无功电压支持，以便在小扰动情况下保证机组与电网的电压稳定性。图1是单台永磁直驱风力发电机与无穷大系统的接线连接图，采用较为广泛的是PV及QV曲线分析法。

图1 直驱风机连接无穷大系统电压分析简图

2 直驱机组风电场数学模型

2.1 永磁直驱风力发电机数学模型

在dq坐标系下，建立的永磁同步发电机组数学模型为［15］

式中，id和iq分别为发电机的d轴与q轴电流;Ld和Lq分别为发电机的d轴和q轴电感;Ra为定子电阻;ωe为电角频率;ωe=npωg，np为发电机转子极对数;ψ0为永磁体的磁链;ud为ug的d轴分量;uq则为ug在q轴的分量。定义q轴的反电势eq=ωeψ0，d轴的反电势为ed=0，假设发电机d轴与q轴电感相等，即Ld=Lq=L，则式(2)可以写成式(3)。

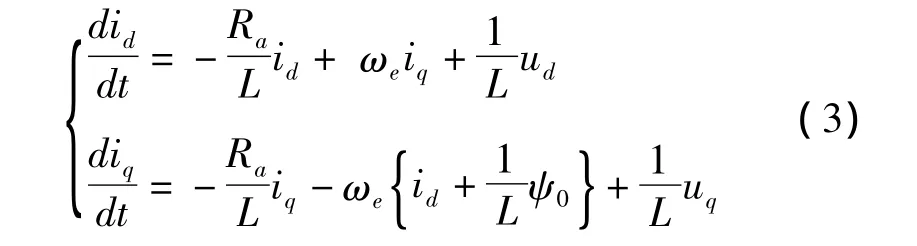
直驱风电机组的电磁转矩表达式为

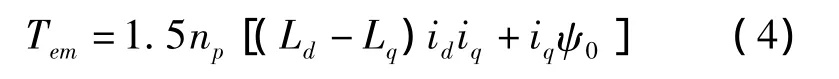
若Ld=Lq=L，则式(4)可以简化为

充分发挥病虫害专业化防治服务组织的作用，适时组织开展应急防治，提高防治效率、效果和效益，解决小麦赤霉病预防控制窗口期短、时效性强等问题。

2.2 直驱机组风电场模型处理

根据直驱风电机组变频器控制策略的不同，当直驱机组风电场(即该风电场全部由同步直驱风电机组构成，下同)恒功率因数控制方式时，其等效于火电机组发有功的同时，吸收或发出一定的无功，此时在潮流计算中将风电场模型处理为PQ节点［16］，同理，直驱机组风电场采取恒电压控制方式时，将风电场模型处理为PV节点。则含风电场的等值系统见图2。图2中，平衡点恒定电压标幺值U2∠0°。

图2 风电场等值系统

风电场经变压器jXb升高电压，经输电线路Z2=R2+jX2接入系统;风电场低压侧电压为U1∠δ。

3 算例分析

3.1 新疆某地区电网概况

新疆中部地区风力资源较为丰富，目前在该地区建成的风电场一期与二期共包括66台单机1.5 MW的直驱风电机组，总容量为99 MW。该地区电网处在电网的中部，是新疆主电网的枢纽，该地区主要电源为吐鲁番电厂，将整个风电场等值处理为两台较大直驱同步机组，风机出口经箱式变压器(690 V/35 kV)升压，集电线路采取直埋电缆与架空线混合的形式送至风电场升压主变压器(35/110 kV)，升压后经过50 km单回输电线路(LGJ－200)送至110 kV小草湖变电站。吐鲁番地区电网与风电场的地理接线图如图3所示。

图3 直驱风电场与某地区电网的地理接线图

3.2 仿真结果及分析

本算例选取吐鲁番地区电网2008年冬大运行方式，风电场接入小草湖变电站，在整个地区电网负荷缓慢增加时，以风机机端、风场升压站、风电场接入点、发电厂母线和中枢变电站母线以及电网末端神泉变电站母线电压作为电压监测点，绘制了吐鲁番电厂220 kV母线、托克逊110 kV母线及神泉变电站110 kV母线作为重点监测母线，分别就以下不同算例做连续潮流计算。上述风电场接入系统后，在全网负荷成倍增长的方式下，绘制了重要节点的PV曲线，以分析系统的静态电压稳定性，如图4所示。图4中，P为风电场发出的功率;U为节点电压。

1)基于直驱机组并网风电场采用恒功率因数(cosφ =1)控制方式

图4 风电场恒功率因数1控制模式下的各变电站P－V曲线

图5 风电场恒功率因数1控制模式下的并网点V－Q曲线

表1 风电场恒功率因数1控制模式下风电场出力与风电场并网点电压对应关系表

风电场的功率注入改变了地区电网各变电站之间的潮流流向，使各线路传输功率大小发生改变，各变电站母线电压的变化趋势是先升后降，但总体均未出现电压越限的情况。在风电场出力水平由0逐渐增加到49 MW时，其为风电接入地区的负荷供电，减少了由吐鲁番主网馈送至风电接入地区的传输功率，减少了线路的无功损耗，使各变电站母线电压有所上升。但随着风电场的出力不断增大，风电接入地区与吐鲁番电网潮流反向，风电接入地区开始由受端系统变为送端系统，随着线路传输功率的不断增加，无功损耗不断增大，最终引起各站电压水平出现下降的趋势，由表1也可以看出。

表2 风电场恒功率因数1控制模式下风电场出力与风电场并网点无功裕度对应关系表

由图5风电场并网点的V－Q曲线可以看出，当风电场出力为49.5 MW时，其并网点的无功裕度为80 Mvar，如表2所示。但随着风电场注入功率的不断增大，并网点的无功裕度呈逐渐减少趋势。在风电出力为99 MW时，同样由表2其无功裕度仅为13 Mvar左右。这同样说明随着风电场注入功率的增大，线路消耗的无功功率增加，系统无功功率匮乏。综上所述，从P－V曲线及对应的V－Q曲线可以得出一致的结论:随着风电场注入功率的增加，地区电网的电压稳定裕度减小。

2)基于直驱机组并网风电场采用恒功率因数(cosφ =0.99滞相)控制方式

将风场内所有的永磁直驱风电机组的功率因数设置为恒功率因数滞相0.99运行，所计算出的各变电站P－V变化曲线如图6。图7为对应风电场并网点的V－Q曲线。

图6 风电场功率因数滞相0.99控制模式下的各变电站P－V曲线

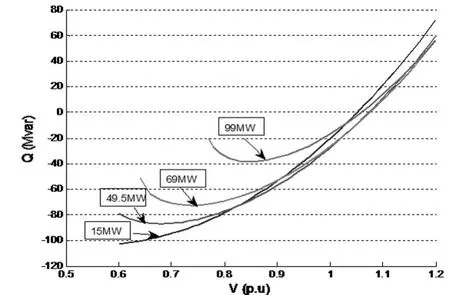
图7 风电场功率因数滞相0.99控制模式下的并网点V－Q曲线

由P－V曲线可以看出，当所有直驱风电机组采取恒定功率因数滞相0.99运行时，各变电站的电压总体也是先升后降。但是与恒定功率因数1的计算相比，由于滞相运行后风电机组发出有功的同时，也在发出一部分无功功率，导致部分变电站母线电压超过了标准规定的电压上限。与之对应风电场并网点V－Q曲线也得出了一致的结论:和恒定功率因数1方式相比，在风电场出力为99 MW时，恒定功率因数1运行时无功裕度为13 Mvar，功率因数滞相0.99运行时，由表3可以得出，无功裕度增大为38 Mvar，电网的无功裕度充足，导致部分母线电压越限。因此在实际电网出现此方式运行时，不建议直驱机组并网风电场采取滞相功率因数运行。

表3 风电场功率因数滞相0.99控制模式下风电场出力与风电场并网点无功裕度对应关系表

3)基于直驱机组并网风电场采用恒功率因数(cosφ = －0.99进相)控制方式

将风场内所有的永磁直驱同步风电机组的功率因数设置为恒功率因数进相0.99运行，图8为计算出的各变电站P－V变化曲线，从图8可以看出，随着风电场有功出力增加，各变电站母线电压幅值逐渐降低，但总体均在规定的电压范围内，只是在风电场出力大于80 MW时，机端与风电场升压站电压出现越下限的情况。

图9为与之对应风电场并网点的V－Q曲线，风电场注入系统功率越大，其无功裕度越小，在风电场出力水平为69 MW时，其无功裕度约为40 Mvar，在出力水平相同时，恒功率因数1的无功裕度为近60 Mvar，由此可见，直驱风电机组进相功率因数运行时，其无功功率裕度减少了约20 Mvar。这是因为，进相运行使直驱风机在发出有功的同时，吸收电网的无功功率，导致整体电压偏低。

4)基于直驱机组并网风电场采用恒电压控制方式

图8 风电场功率因数滞相0.99控制模式下的各变电站P－V曲线

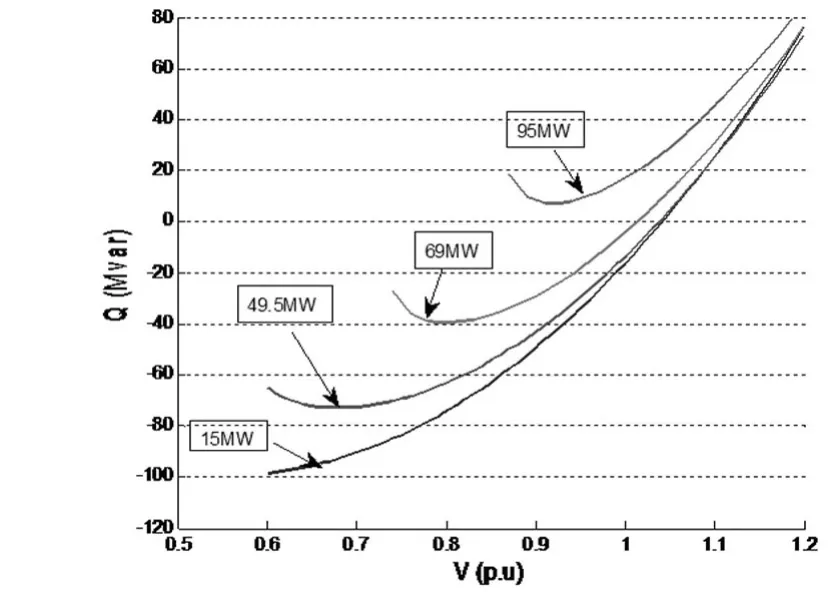
图9 风电场功率因数滞相0.99控制模式下的并网点V－Q曲线

图10 风电场恒电压控制下各变电站P－V曲线

由图10的P－V曲线明显可以看出，当直驱机组采取恒电压控制方式运行时，直驱机组机端电压始终为1.0 p.u.。风电场注入系统功率在100 MW以内时，地区电网各变电站母线电压均在规定的偏差范围内，不会出现越上限或越下限的情况。与之前的恒定功率因数下的电网电压稳定水平相比，显而易见，基于直驱机组风电场采取恒电压控制方式的系统静态电压稳定性要优于恒定功率因数控制方式下的电网电压稳定性。

图11 风电场恒电压控制下并网点的V－Q曲线

从图11并网点的V－Q曲线也可以看出，风电场出力水平分别为15 MW、69 MW、99 MW时，其对应的电网无功裕度相差不大。这是由于直驱风电机组网侧变频器采取恒电压的控制策略。在实际运行中风电场相当于电网中的PV节点，随着机组出力的增加，当机端电压或电网电压有变化时，直驱风电机组的无功功率可以在较大范围内变化调整，以保证机组端电压始终为1.0 p.u.，使电网电压近似维持不变。这也是恒电压控制方案下所得出的风电电力系统电压静态稳定性好的原因。

4 结论

风电场穿透功率的增加使其对电网的影响逐渐扩大。尤其是在风电场与电网弱联系时，其对地区电网电压稳定性的影响不容忽视。通过调整直驱机组风电场的不同控制策略，其对含直驱机组风电场的系统静态电压稳定性进行了详细研究，得出的结论如下。

①风电场在处于低出力水平时，可以较好地改善地区电网的静态电压稳定性。但随着风电场注入功率的增加，线路的无功损耗增大，致使风电场接入地区需要从地区主网受入大量无功功率，电网无功裕度减少，最终导致电网静态电压稳定性降低。

②基于直驱机组并网风电场采取恒功率因数与恒电压两种调控方案相比，恒电压控制方式下含直驱机组风电场的电压稳定性要优于恒功率因数控制方式下的。

［1］王承煦，张源.风力发电［M］.北京:中国电力出版社，2008.

［2］Ki－Chan Kim，Seung－ Bin Lim，Ki－ Bong Jong，Sung－Gu Lee，Ju Lee，Yeoung－Gyu Son ，Young－Kil Yeo，Soo－ Hyun Baek.Analysis on the Direct－ Driven High Power Permanent Magnet Generator for Wind Turbine［J］.2008，243 －247.

［3］周双喜，朱凌志，郭锡玖，等.电力系统电压稳定性及其控制［M］.北京:中国电力出版社，2004.

［4］王海超，周双喜，鲁宗相，等.含风电场的电力系统潮流计算的联合迭代方法及应用［J］.电网技术，2005，29(18):59－62.

［5］张义斌，王伟胜，戴慧珠.基于PV曲线的风电场接入稳态分析［J］.电网技术，2004，28(23):61 －65.

［6］吴俊玲，周双喜，孙建锋，等.并网风力发电场的最大注入功率分析［J］.电网技术，2004，28(20):28 －32.

［7］Chai Chompoo － inwai，Wei－ Jen Lee，Fuangfoo P，et al.System Impact Study for the Interconnection of Wind Generation and Utility System［J］.IEEE Transactions on Industry Applications，2005，41(1):163 －168.

［8］HA L T，SAHA T K.Investigation of power loss and voltage stability limits for large wind farm connections to a subtransmission network［C］.Power Engineering Society General Meeting，IEEE，Vol 2，Jun 6 － 10，2004，Denver，USA.2004:2251 －2256.

［9］SMITH J，BROOKS D.Voltage impacts of distributed wind generation on rural distribution feeders［C］.Transmission and Distribution Conference and Exposition，IEEE/PES，Vol 1，Oct 28 －Nov 2，2001，Atlanta，USA.2001(1):492 －497.

［10］Le Thu Ha，Tapan Kumar Saha.Investigation of power loss and voltage stability limits for large wind farm connections to a subtransmission network［J］.IEEE，2007.

［11］Magnip P .Large－scale wind power integration and voltage stability limits in regional networks［C］.IEEE power engineering society summer meeting，2002.

［12］于德龙，赵海翔，曹娜.风电场接入地区电网的电压问题分析［J］.中国电力，2006，39(6):10－14.

［13］张红光，张粒子.风电场接入电网的安全稳定分析［J］.中国电力，2007，40(5):105 －109.

［14］迟永宁，刘燕华，王伟胜，陈默子，戴慧珠.风电接入对电力系统影响的研究［J］.电网技术，2006，48(5):38－44.

［15］杨国良，李惠光.垂直轴永磁同步风力发电系统建模及瞬时功率控制策略［J］.电力自动化设备，29(5)，39－42.

［16］林莉，孙才新，王永平，等.大容量风电场接入后电网电压稳定性的计算分析与控制策略［J］.电网技术，2008，32(3):41 －46.