风浪联合作用下的海上单桩基础风力发电机组动力响应分析
贺广零,仲政
(1.同济大学力学博士后流动站,上海市,200092;
2.中国电力工程顾问集团华北电力设计院工程有限公司,北京市,100120; 3.同济大学航空航天与力学学院,上海市,200092)
0 引言
近年来,伴随着全球海上风电场大规模建设的趋势,我国海上风能技术亦获得了高度重视与迅猛发展。然而,由于根基薄弱与底蕴不足,迄今我国海上风能技术还不够成熟。就海上风机基础而言,现有的研究成果以拟静力分析为主[1-2],不考虑动力效应,存在低估结构响应、荷载组合困难等难题。已有部分学者[3-4]尝试进行海上风力发电机组结构动力响应分析,但并未给出合理的风浪耦合机制,所采用的结构模型亦显粗糙,与工程应用相去较远,参考价值不大。有鉴于此,本文提出一种相对合理的风浪耦合机制,结合实际工程中的海上风力发电机组结构模型,进行结构在风浪联合作用下的动力响应分析,以正确评估结构的动力效应。
1 环境荷载模型
海上风力发电机组外部环境十分复杂,不仅承受风、海浪和地震作用,还与浮冰、海流、潮汐和冲刷等因素相关。而风力发电机组也有自己的运行状态及多种失效模式。对于不同的运行状态,受到不同外部激励时所产生反应各不相同(强度破坏或疲劳失效等)。由于风力发电机组环境荷载和运行状态自身的复杂性,加上两者的随机耦合,就导致应用典型规范需要考虑诸多工况。在现有的理论模型中,还很难把所有环境荷载的相关性考虑完整,只能考虑主要荷载,如风和海浪的共同作用等。
1.1 随机Fourier风谱模型
基于随机过程的随机函数描述,引入截尾函数,则随机Fourier谱[5]可定义为
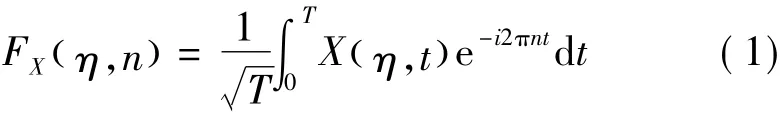
式中:T为样本持时;随机过程X(η,t)是样本x(t)的集合,η为影响随机激励发展过程且具有物理意义的随机变量或随机向量。根据各向同性紊流理论,可确定随机Fourier谱的基本表达式。依据随机建模准则,由310组实测风速数据记录,可以给出基本随机变量的概率分布和待定拟合参数的具体值,并最终确定随机Fourier谱的表达式[6]为
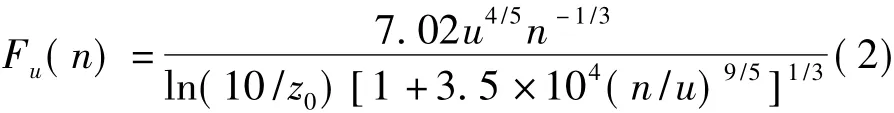
式中:u为10 m高平均风速,服从极值I型分布;z0为地面粗糙度,服从对数正态分布。显然,塔体上任意一点处脉动风速的随机特性可以通过随机Fourier谱来体现。与塔体不同的是,桨叶在运行过程中存在显著的旋转效应,将会对风速场产生很大的干扰。本文采用基于物理机制的旋转Fourier谱来考虑脉动风速的旋转效应[7-8]
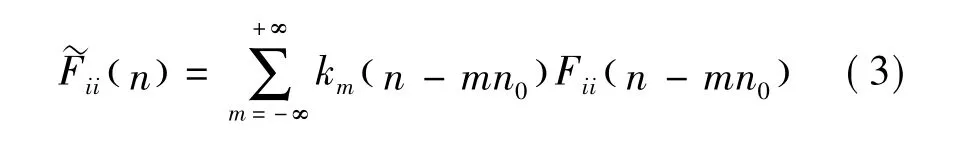
式中:Fii(n)为随机Fourier谱;~Fii(n)为旋转Fourier谱;km(n)为衔接二者的旋转模态。事实上,旋转Fourier谱为作用在旋转桨叶上的风速的相关函数经过Fourier变换所得,是一种自身蕴含了桨叶旋转效应的紊流风速谱。
对随机 Fourier谱与旋转 Fourier谱进行逆Fourier变换,即可分别获得塔筒与叶片上的风速时程,具体步骤详见文献[8]。海上风力发电机组叶片结构颇为复杂,且存在显著的旋转效应、风剪效应、尾流效应等,本文引入广泛接受的叶素动量(blade elementmomentum)理论[9-10]以准确而简单地确定作用在叶片上的风荷载,并考虑旋转桨叶对风速的减缓作用。对于作用于塔筒上的风荷载,可借鉴建筑结构领域的相关研究成果确定[10]。
1.2 随机Fourier海浪谱模型
将海浪视为一个平稳的随机过程,自然地可以引入功率谱的概念描述波能及其频域分布特征,但更为合理的方式是依据风生波的物理机制发展Fourier海浪谱模型。基于拟层流风波生成机制,即给定频率处海浪谱的能量等于具有该频率的谐波自具有对数剖面的平行气流中汲取而来,文献[11-12]建立了随机Fourier海浪谱模型。
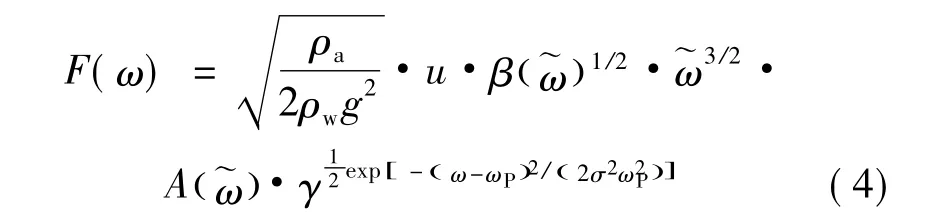
式中:设10 m高、10 min平均风速u1为等效风速u,m/s;=μω/ωP,ωP为峰值频率,μ为谱峰频率调整系数;β()为能量传递系数;A()为波幅;γ为谱峰值调整系数;σ=σL(ω<ωP)和σ=σR(ω>ωP)为谱形参数;ρa为空气密度,kg/m3;ρw为水密度,kg/m3;g为重力加速度,m/s2。
由于随机Fourier海浪谱基于随机过程的随机函数表示建模,对其进行逆Fourier变换,并考虑随机相位由随机初相位和相位差谱确定,采用式(4)生成海浪时程。
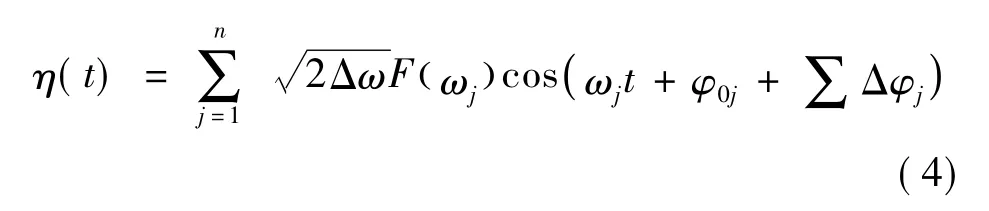
式中:F(ωj)为随机Fourier海浪谱模型在离散点处的值;φ0j为随机初相位;Δφj为相位差谱;n为离散点数目。
根据文献[13],如果构件直径与波长相差很大(D/L<0.2),则可采用Morison公式来计算结构所受波浪荷载。本文所采用的模型直径最大为6 m,为小尺度结构物,其对波长的影响不明显,故采用Morison公式计算结构承受的波浪力是合理的。该模型将波浪力分为惯性力和拖拽力2个部分,前者与水质点运动的加速度有关,后者与水质点的速度有关。在Morison公式中,作用在单位长度直立圆柱上的波浪力为
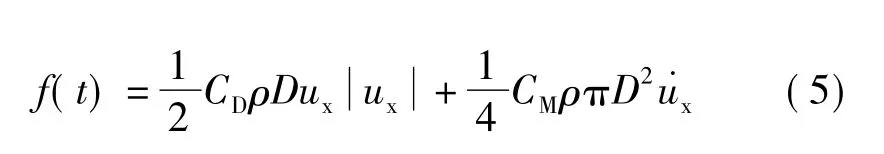
式中:CD是拖拽力系数;CM是质量系数;ρ是海水的密度,kg/m3;ux为质点水平速度,m/s;˙ux为质点水平加速度,m/s2,由选用的波浪理论确定。
1.3 风浪耦合物理机制
风浪耦合一直是海洋工程研究的难点。文献[13-16]对风浪耦合都有相应规定,其内容均具备复杂性、多样性与保守性的特点。显然,上述规范之所以存在这些共性,是因为风浪耦合的物理机制尚不明确。在无法把握物理机制的情况下,可以尝试建立半经验关系。Neumann和Pierson[17-18]给出了有效波高与平均风速之间的半经验关系,Ochi[19]研究了飓风条件下二者之间的关系,以实现风浪耦合。然而,半经验关系成立的前提条件比较苛刻,例如要求海洋状态必须充分发育,且仅适用于深海区域,否则将会导致较大的误差。另外,一些学者意图纯粹从数学角度来实现风浪耦合。其中,较为成功的是Turkstra法则[20-23]与多元极值理论[24]。Turkstra法则本质上是将控制荷载的最大值与其他荷载时程进行随机组合。由于Turkstra法则是基于工程经验提出的一种组合规则,尽管有效地简化了荷载组合过程,但它却很有可能低估荷载组合值[22,25]。多元极值理论是研究多个相关变量极值性质的理论,探讨了确定多个相关变量极值联合分布的方法,是考虑各种极端荷载共同作用的有效手段,在海洋工程中获得了广泛应用[26-27]。但由于多元极值分布中相关结构较为复杂,其相关函数多为隐式形式,只能通过繁杂的迭代求解,不利于工程应用。
应该强调,在一般的荷载(荷载效应)组合中,对不同荷载的效应最终通过若干组合系数或某种特殊组合方式[平方和开平方(square root of the sum of the squares,SRSS)]等来根据单个荷载(荷载效应)的极值获得共同作用时的极值,这在本质上是拟静力分析与设计的结果。正因为仅仅进行拟静力分析,才出现各个荷载的极值通常不同时出现,因而不能简单相加,由此导致荷载(荷载效应)组合的各种理论或方式。事实上,由于荷载与荷载效应是非线性的且不具有简单的叠加性质,最大荷载组合与最不利效应之间不能建立一一对应的关系,因此上述组合方式在考虑非线性的情况下也是不适用的。更为普遍适用的方法是进行多种随机作用下的结构随机动力反应分析。在直接动力分析中,对不同随机荷载按照上述方式进行加权组合既无必要、也不正确,一种简单且有效的方法是基于物理机制来实现荷载组合。在本文所采用的随机Fourier风速谱和随机Fourier海浪谱模型中,它们的基本物理参数集分别为{u,z0}和{u,ωP,γ,μ,σL,σR}。可以看出,风和海浪的基本物理随机变量有1个相同的参数u,而正是这个共有的参数给出了风与海浪之间的物理关系,揭示了风浪耦合的物理机制。这样,风浪耦合可以通过考虑其随机Fourier谱中基本参数的耦联来生成风速和海浪时程。
2 一体化结构模型
所谓风力发电机组一体化结构模型,是指将桨叶、机舱、塔体和基础同时建模,以模拟结构自身构件以及结构与其他介质之间的动力相互作用,包括不同构件(尤其是叶片与塔体)之间的动力相互作用、土-结构动力相互作用、气弹效应等,并反映结构应力集中、局部屈曲等细部特征。总体上,风力发电机组一体化建模的目的在于构建精细化的结构模型,把握准确的结构动力特性,获取精确的结构动力响应。海上风力发电机组结构如图1所示。
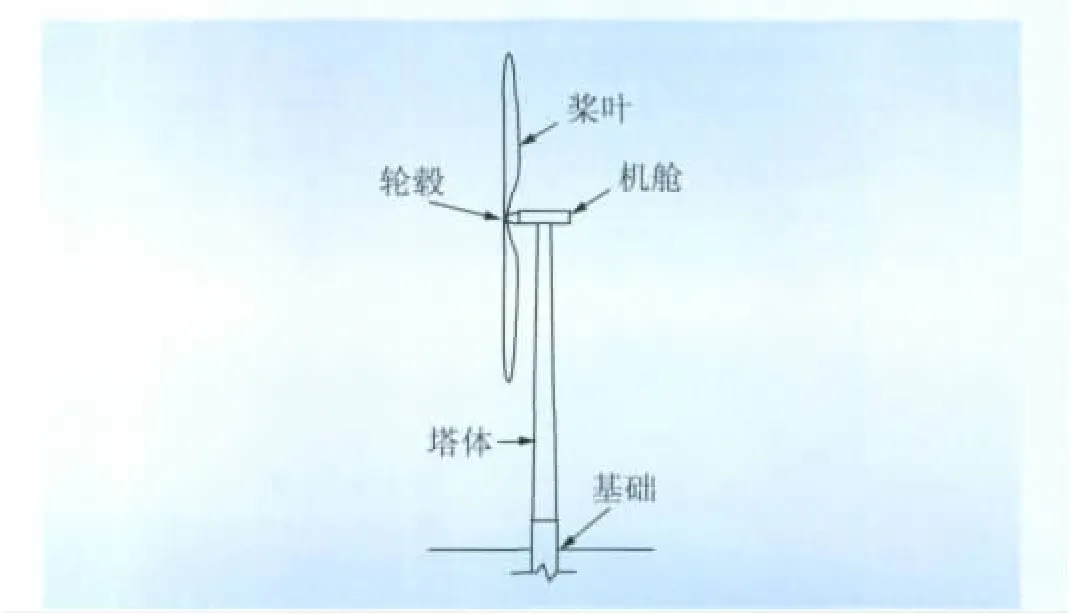
图1 海上风力发电机组结构Fig.1 Offshore wind turbine system
与陆上风力发电机组不同的是,海上风力发电机组囿于环境条件,需要采用独特的基础形式,以满足承载力与正常使用要求。重力式基础、单桩基础、多脚架基础、导管架基础与高桩承台基础均为常见的海上风机基础形式,其中又以单桩基础应用最为广泛。纵观常见的海上风机基础,大部分需要采用超大直径钢管桩。然而,由于土体动力弱化效应、土塞效应等现象的存在,迄今尚未出现适合超大直径钢管的桩土模型。由于在分析与设计过程中未全面考虑这些因素,已建成的海上风机基础(尤其是单桩基础)均出现了或多或少的倾斜现象。其中,部分风机基础因倾斜过大,导致风力发电机无法正常运行。土体动力弱化效应是指在循环荷载下桩周土体刚度随着循环次数的增加而降低。文献[14]明确规定需考虑该效应,但未给出具体的分析方法。在考虑土体动力弱化效应的分析方法中,最常见的是文献[15]建议的p-y曲线分析法。首先,该法主要基于循环次数少于200次的现场实验,而循环次数大于200次时,土体动力弱化现象并未终止[28-29]。其次,该法中的p-y曲线是基于小直径桩基础(桩径小于1.5 m)现场实验所得[30-31],故而该法并不适用于超大直径桩基础(桩径超过3 m),且极有可能低估其动力响应[32-33]。为此,Juirnarongrit和Ashford[34]研究了基桩尺寸对p-y曲线的影响,提出了考虑尺寸效应的p-y曲线法,本文即采用此模型进行分析。在有限元模型中,桩-土相互作用可采用弹簧单元来模拟:水平方向桩土相互作用采用水平弹簧,其刚度定义根据p-y曲线来求得;竖向桩土相互作用采用竖向弹簧,其刚度利用t-z曲线来确定;端部弹簧根据q-z曲线来确定其刚度。弹簧模型原理如图2所示。
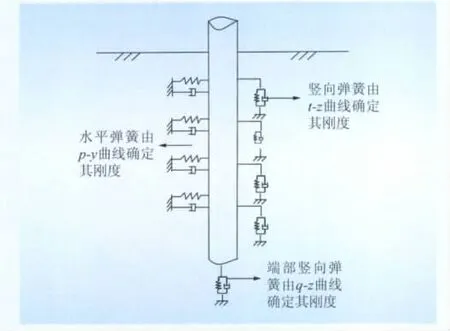
图2 桩-土相互作用有限元模型Fig.2 Finite elementmodel of pile-soil interaction
3 工程实例
以我国东海海域某一具有可行性的场址为例,结合我国某知名风机厂家提供的3.6 MW海上风力发电机组,进行海上风电机组结构在风浪联合作用下的动力响应分析。
3.1 工程地质与海洋水文
本场地最大勘探揭露深度约为80 m,揭露的地基土层按地质时代、成因类型、土性的不同和物理力学性质的差异可分为7个大层,其中⑤层、⑦层各分为2个亚层,⑦1层又分为2个次亚层。各土层的埋藏条件及工程地质特性详见表1。海底较平缓,在潮流作用下以淤积为主,滩面表层主要为淤泥,局部夹薄层粉土。本建筑场地属于Ⅳ类,场地沿线属于抗震不利地段。
海底高程为-10.00~-10.67 m(国家85 m高程),平均海平面高程0.23 m。平均高潮位为1.86 m,平均低潮位为-1.34 m,设计高潮位为2.55 m,设计低潮位为 -2.09 m。场址区相应历史最高潮位为4.02 m,历史最低潮位为-2.87 m。本海区设计潮流流速中,表层流速为315 cm/s,中层流速为257 cm/s,底层流速为148 cm/s,流速平均值为239 cm/s。平均波高为2.83 m,波周期为7.76 s,波长为74.1 m,波速为9.55 m/s,累积率1%的波高H1%为5.81 m,累积率4%的波高H4%为5.06 m,累积率5%的波高H5%为4.82 m,累积率13%的波高H13%为4.24 m。
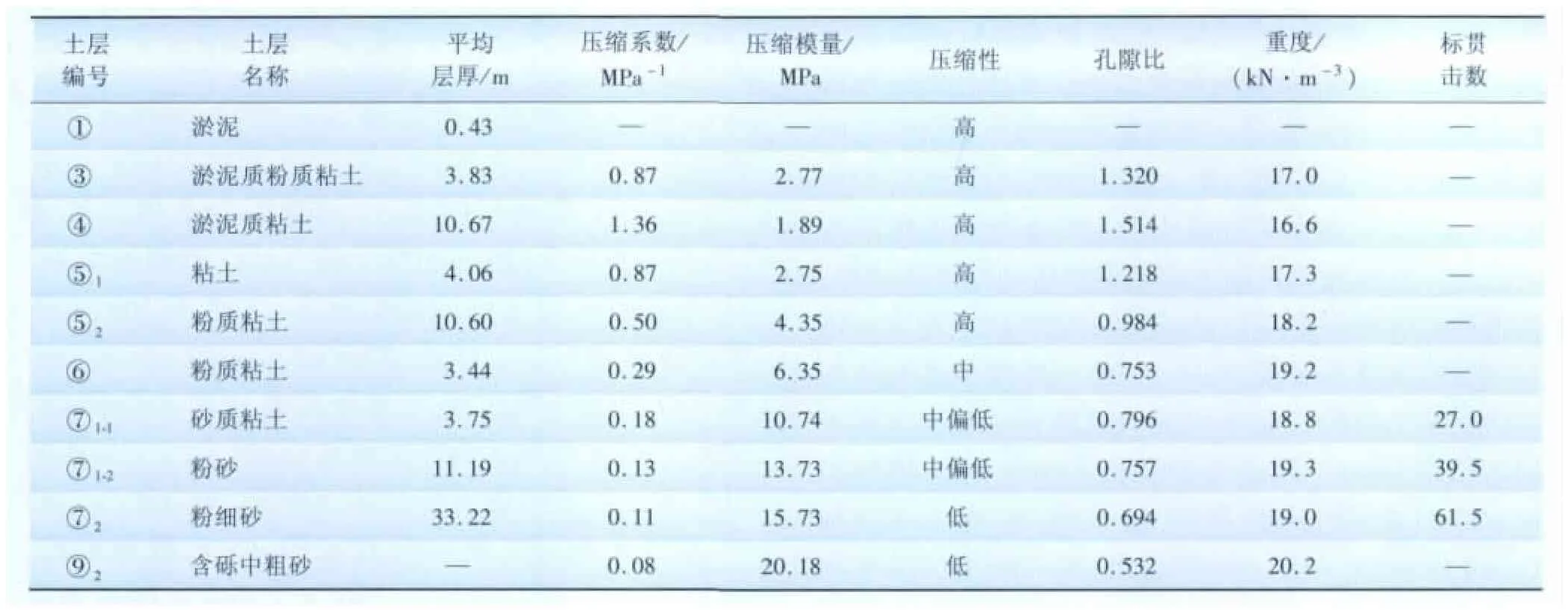
表1 地层特性表Tab.1 Formation characteristics
3.2 结构模型
以我国某知名风机厂家提供的W 3600M-116型海上风力发电机组(装机容量为3.6 MW)为例进行分析。风轮直径为116 m,轮毂中心到塔低的高度为80 m,轮毂中心到平均海平面高度为90 m。组装后风轮的质量为95 t,机舱质量为140 t,塔筒共4节,总质量为284 t,塔筒顶部直径为3.815 m,塔顶壁厚为66 mm,底部直径为5 m,塔底壁厚为88 mm。基础采用单桩基础,钢管桩直径6 m,桩长65 m,壁厚75 mm,入土深度约50 m,桩尖高程为-62 m,桩尖进入第⑦2层粉细砂层,桩顶高程为3 m。操作平台高程为11 m。单桩基础与塔筒之间设连接段钢管过渡,连接段钢管四周设置靠船设施、钢爬梯及平台等,连接段钢管顶面通过法兰与风机塔筒连接,连接段钢管下端通过高强灌浆连接方式与钢管桩连接,并设置剪力栓。整体结构尺寸如图3(a)所示。
以大型通用有限元软件ANSYS为建模平台,建立海上风力发电机组一体化有限元模型,如图3(b)所示。因叶片和塔筒1个方向的尺寸与另外2个方向的尺寸相差较大,同时叶片在工作状态下具有显著的应力刚化现象,故叶片和塔筒都采用了能较好体现这些特征的八节点壳体单元(SHELL 91)。在整体分析过程中,机舱及其内部构件可视为一个整体,可借助梁单元(BEAM 189)来模拟。单桩基础依据PIPE 59单元和PIPE 16单元共同来体现。PIPE 59单元专门用于模拟浸没在水中的杆件,可以很好地模拟海浪、海流对单桩基础的作用。因此,采用PIPE 59单元模拟单桩基础在水中的部分,对于泥面以下桩柱则采用PIPE 16单元来模拟。如前文所述,桩土相互作用通过非线性弹簧单元COMBIN 39来刻画。在有限元模型中,划分的PIPE 59单元和PIPE 16单元尺寸为0.1 m,COMBINE 39弹簧单元每隔0.5 m设置1组,遇土层分界点加设1组弹簧单元。
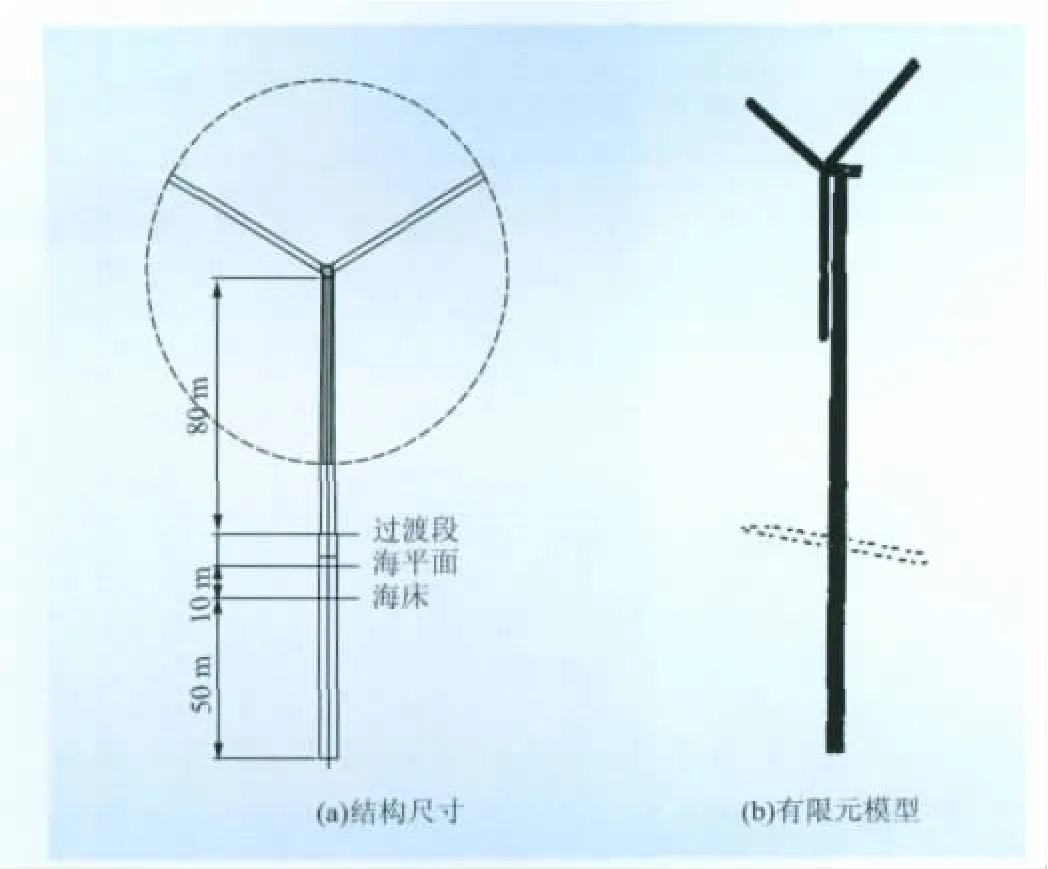
图3 海上风力发电机组整体结构Fig.3 Integrated model of offshore w ind turbine system
3.3 结构动力响应分析
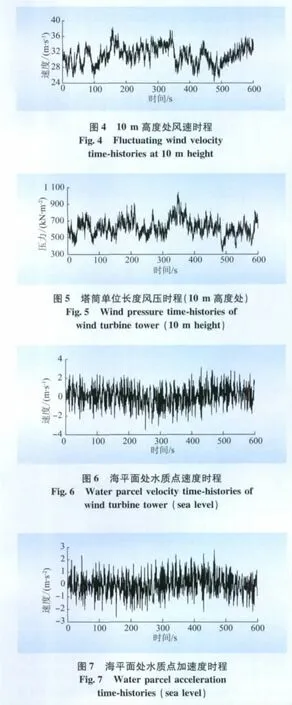
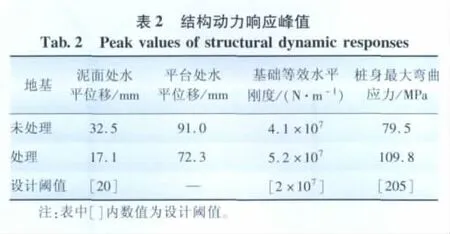
依据拟建风电场址的风场以及水文地质资料,可确定其基本风速 u为31.2 m/s(对应风压为0.6 kPa),地面粗糙度z0可取为1 mm[13],波浪峰值频率ωP为0.566,谱峰值调整系数γ为8.274,谱峰频率调整系数μ为1.728,谱形参数σL和σR分别为0.161和0.764。依据上述物理方法,模拟特定环境条件下的风速时程(图4)、风压时程(图5)、水质点速度时程(图6)、水质点加速度时程(图7)以及波浪力时程(图8),将风压时程、波浪力时程作用于海上风力发电机组一体化结构模型上,利用有限元动力分析方法,进行在风浪联合作用下的结构动力响应分析,可获得泥面处的水平位移动力时程响应、平台处的水平位移时程响应、桩身弯曲应力时程响应分别如图9~11所示,并进而获得结构动力响应最值(表2)。在分析过程中,采用瑞利阻尼[35]。考虑到风力发电机组的底阻尼特性,结合美国学者Prowell等的实验结果[36-37],本文取阻尼比0.6%。
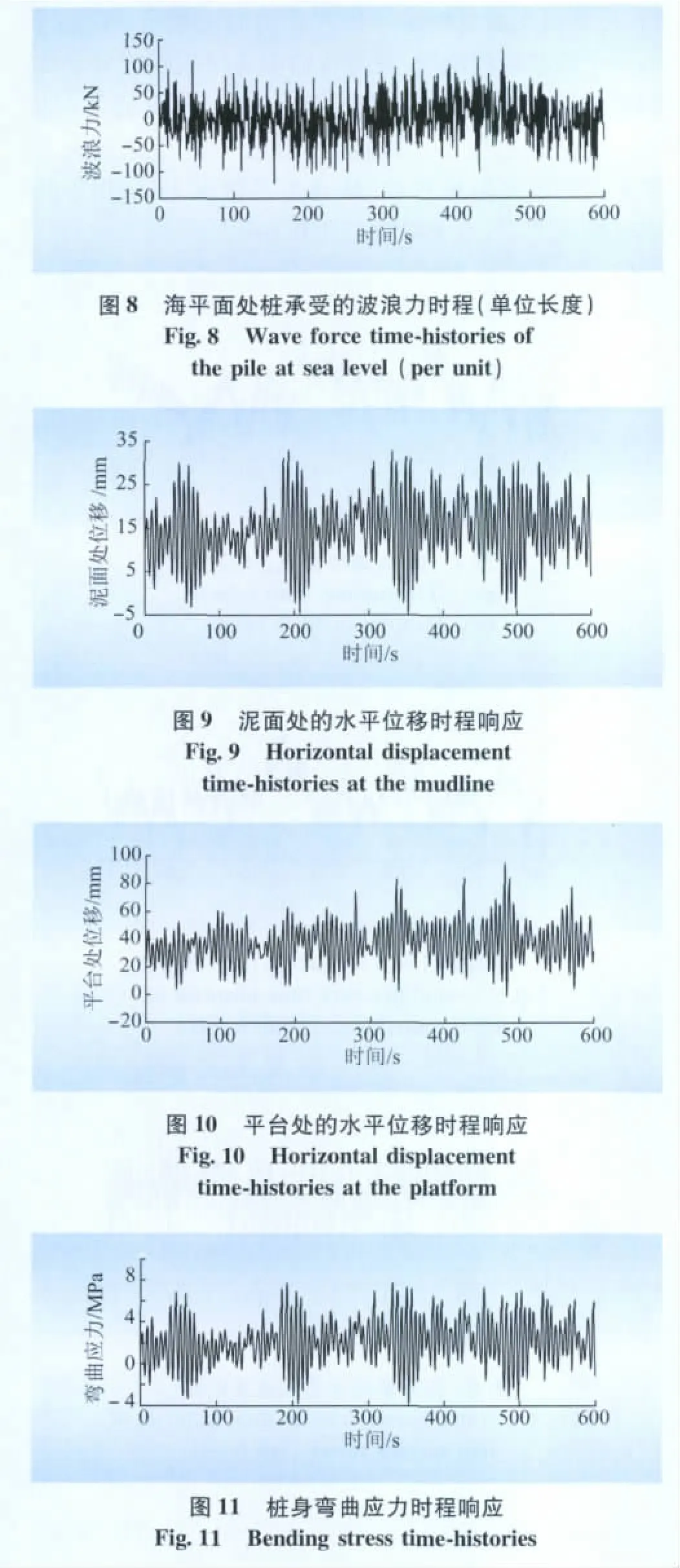
根据西欧各地区海上风机基础的设计与施工经验,单桩基础适用于水深约为15m、地基土为中等密实土体及土层的内摩擦角在30°以上的环境条件。事实上,西欧各地区能满足上述条件的海域颇为宽广,加上单桩基础的经济性与简洁性,单桩基础在诸多海上风机基础中应用最为广泛。与之不同的是,我国各海域的地质条件较为薄弱,例如,本海域海床上部土层为粉质粘土及粉砂,地基刚度相对较小。为了验证对单桩基础进行地基处理的必要性,本文就地基未处理以及地基处理2种情况进行了对比分析(表2):(1)地基未处理,按原有地质条件进行分析;(2)地基处理,对海床5 m深度范围内的土体进行注浆碎石加固,围绕桩身位置填筑出一个高约为5 m、顶边半径为15 m、坡度为1∶1的圆台体,碎石顶表面铺1层高强土工网装碎石(直径大于150 mm的碎石占80%以上)以防水流冲刷。研究表明,若未进行地基处理,泥面处水平位移以及平台处水平位移均偏大,从而引起单桩基础的转角偏大,最终导致海上风力发电机组倾斜过度而无法正常运行。值得说明的是,在实际工程中,这种由单桩基础转角过大而导致海上风力发电机组无法正常运行的现象屡见不鲜。究其原因,在于对海上风力发电机组在风浪联合作用下的动力效应与时间效应认识不足,尚未明确2种效应导致的地基弱化现象。为此,有必要研究海上风力发电机组的精细化荷载模型与结构模型(尤其是桩土模型),并辅以必要的地基处理方法,方可确保结构可靠稳定。
4 结论
(1)基于随机过程的随机函数描述,给出了风速与海浪随机物理模型,即随机Fourier风速谱与随机Fourier海浪谱。依据随机物理模型中共有随机变量的耦联关系,提出了基于物理机制的风浪耦合方法。
(2)鉴于海上风电机组单桩基础采用超大直径管桩,引入了适用于超大直径管桩的桩土相互作用机制,构建了海上风力发电机组一体化结构模型。
(3)以我国东海海域某具有可行性的场址为例,结合我国某知名风机厂家提供的3.6 MW海上风力发电机组,进行海上风电机组结构在风浪联合作用下的动力响应分析,并对工程设计给出了若干建议。
[1]黄维平,刘建军,赵战华.海上风电基础结构研究现状及发展趋势[J].海洋工程,2009,27(2):130-134.
[2]李静,陈健云.海上风力发电结构动力研究进展[J].海洋工程,2009,27(2):124-129.
[3]李德源,刘胜祥,张湘伟.海上风机塔架在风波联合作用下的动力响应数值分析[J].机械工程学报,2009,45(12):46-52.
[4]李德源,刘胜祥,张湘伟.风波联合作用下的风力机塔架疲劳特性分析[J].太阳能学报,2009,30(10):1250-1256.
[5]Li J,Chen JB.Stochastic dynamics of structures[M].Singapore: John Wiley&Sons,2009:1-216.
[6]李杰,张琳琳.实测风速资料的随机Fourier谱研究[J].振动工程学报,2007,20(1):66-72.
[7]贺广零,李杰.风力发电高塔系统基于物理机制的旋转样本功率谱研究[J].中国电机工程学报,2009,29(26):85-91.
[8]贺广零,李杰.风力发电高塔系统风场模拟[J].同济大学学报,2010,38(7):976-981.
[9]Burton T,Sharpe D,Jenkins N,et al.Wind energy handbook[M].Chichester:John Wiley&Sons,2001:41-172.
[10]贺德馨.风工程与工业空气动力学[M].北京:国防工业出版社,2006:80-91.
[11]徐亚洲,李杰.风浪相互作用的Stokes模型[J].水科学进展,2009,20(2):281-286.
[12]徐亚洲,李杰.近海风力发电高塔波浪随机动力响应分析[J].振动工程学报,2011,24(3):315-322.
[13]Det Norske Veritas.DNV-OS-J101 Design of offshore wind turbine structures offshore standard[S].1st Edition.Oslo,Norway:Det Norske Veritas,2004.
[14]Germanischer Lloyd.Rules and guidelines IV—Industrial services,part2:guideline for the certification of offshore wind turbines[S].Hamburg:Germanischer Lloyd,2005.
[15]American Petroleum Institute.RP2A-WSD recommended practice for planning,designing and constructing fixed off-shore platformsworking stress design[S].API Recommended Practice 2A-WSD,21st edition,Dallas:American Petroleum Institute,2000.
[16]JTS 144-1—2010港口工程荷载规范[S].北京:人民交通出版社,2010.
[17]Neumann G,Pierson W J.Principle of physical oceanography[M].Englewood Cliffs:Prentice Hall,1963:1-24.
[18]Kuhn M J.Dynamics and design optimization of offshorewind energy conversion systems[D].Delft:Delft University of Technology,2001.
[19]Ochi M K.On hurricane-generated seas[C]//Proceedings of the Second International Symposium on Ocean Wave Measurement and Analysis.New Orleans,USA:ASCE,1993:374-87.
[20]Turkstra C J,Madsen H O.Load combinations in codified structural design[J].Journal of the Structural Division,1980,106(12): 2527-2543.
[21]金伟良.工程荷载组合理论与应用[M].北京:机械工业出版社,2006:10-30.
[22]Cheng P W.A reliability based design methodology for extreme response of offshore wind turbine[D].Delft:Delft University of Technology,2002.
[23]陈为飞.近海风机塔架风浪荷载分析[D].杭州:浙江大学,2010.
[24]Coles SG,Tawn JA.Modelling extreme multivariate events[J].J R Statist Soc B,1991,53(2):377-392.
[25]Melchers R E.Structural reliability,analysis and prediction[M].Chichester:John Wiley&Sons,1999:199-215.
[26]刘德辅,董胜.随机工程海洋学[M].青岛:中国海洋大学出版社,2004:89-118.
[27]欧进萍,段忠东,肖仪清.海洋平台结构安全评定:理论、方法与应用[M].北京:科学出版社,2003:12-49.
[28]Hettler A.Deformation responses of rigid and elastic foundations in sand under static and cyclic loadings[D].Karlsruhe:University of Karlsruhe,1981.
[29]Achmus M,Abdel-Rahman K,Kuo Y S.Numericalmodeling of large diameter steel piles under monotonic and cyclic horizontal loading[C]// International Symposium on Numerical Models in Geomechanics(NUMOGX).Rhodes,Greece:Taylor& Francis,2007:453-459.
[30]Cox W R,Reese L C,Grubbs B R.Field testing of laterally loaded piles in sand[C]//Proceedings of the 6th Annual Offshore Technology Conference.Houston,USA:OTC Committee,1974: 459-472.
[31]Reese L C,CoxW R,Koop FD.Analysis of laterally loaded piles in sand[C]//Proceedings of the 6th Annual Offshore Technology Conference.Houston,USA:OTC Committee,1974:473-483.
[32]Achmus M,Abdel-Rahmen K,Peralta P.Analysis of load-bearing behavior of offshore wind turbine foundations[C]//Symposium of Piles 2005.Hannover,German:University of Hannover,2005: 137-158.
[33]Lesny K,Richwien W,Hinz P.Assessment of the offshore wind turbine foundations[C]//Symposium of offshore wind energy,the aspects on the construction and environments.Hannover German: University of Hannover,2007:175-183.
[34]Juirnarongrit T,Ashford SA.Effect of pile diameter on themodulus of subgrade reaction[D].San Diego:University of California,2005.
[35]Clough R W,Penzien J.Dynamics of structures[M].New York: McGraw-Hill,1993:15-17.
[36]Prowell I,Veletzos M,Elgamal A,et al.Experimental and numerical seismic response of a65kW Wind turbine[J].Journal of Earthquake Engineering,2009,13(8):1172-1190.
[37]范洪军,金全州,刘铁英,等.风力机地震响应分析的研究现状与展望[J].结构工程师,2010,26(6):155-163.

