多孔介质流场的热模拟方法
张明宝
(哈尔滨锅炉厂有限责任公司,黑龙江 哈尔滨 150046)
多孔介质流场的热模拟方法
张明宝
(哈尔滨锅炉厂有限责任公司,黑龙江 哈尔滨 150046)
随着工业技术的迅速发展,多孔介质的强化冷却问题已成为工程上及热交换领域里的热门课题。对于多孔介质性能的研究,不仅要关注其散热性能等宏观方面的作用,同时也要考虑其内部流场作用等微观方面的影响。可建立流体力学的数学模型以模拟多孔介质的内部流场,主要从流体力学和热力学的角度对多孔介质的内部流场进行模拟。该方法在较简单模型下的优势并不明显,但在复杂的多孔介质模型中,可简化模型及边界条件的设置,减少建模的时间。
多孔介质;流场;计算;热模拟;热交换;数值;模型;方法
1 概 述
随着工业技术的不断发展,更有效的强化冷却技术已经成为能源领域及热交换领域里的热门课题。欲改进设备的热交换性能,提高热交换的传热效果或者提高燃气轮机的工作效率,通常面临的一个关键问题是如何提高结构的抗高温能力。以多孔介质为载体的发散冷却技术,因其高效率的冷却方式,得到越来越多的重视与关注,然而,在基础理论和实验方法上,多孔介质内传统的传热传质方面还有很多问题是值得研究的。如数学模型的建立和边界条件的确定;冷却介质在微孔中的吸热、流动、相变等问题。另外,对应于发散冷却特性的研究,常局限于分析单一的某个参数对冷却效率的影响,而没有对应于实际应用进行综合分析。随着对发散冷却系统设计要求的提高,如何用较少的冷却介质达到较高的冷却效率,如何组合最佳的多孔材料以满足结构更高的热防护需求……此类问题[7-11],也是发达国家面临的基础科学问题,同时也给国内的科学研究带来新的机遇和挑战。
现探索使用一种全新的方法,从流体力学及热力学的角度出发,求解多孔介质的流场分布问题。依据热场和流场的高度相似性,用热流密度场来模拟多孔介质内部的流场,并给出了具体的算例,比较了两种模拟方法的计算结果。利用此方法,可在复杂的多孔介质建模中,简化模型及边界条件的设置,减少模型的建立时间。同时,还对采用此种建模方法的局限性做了分析。
2 基本理论模型
根据N-S方程(纳维-斯托克斯方程)进行流体计算,而N-S方程极为复杂,至今还无完整的解析解,只能用数值分析的方法,无限逼近求得近似求解。为了简化计算模型,从流体模型的控制方程和离散方法这两方面进行简化分析。
2.1 流体的控制方程
在雷诺平均中,瞬态N-S方程中要求的变量已经分解为时均常量和变量。以速度为例:

式(1)中,Ui和ui′是时均速度和波动分量。其他相似的物理量中,压力和其他标量有:

式(2)中,φ表示一个标量,如:压力、动能或粒子浓度。
用这种形式的表达式,将流动的变量放入连续性方程和动量方程中,并取某段时间的平均值,可以写成连续方程形式:
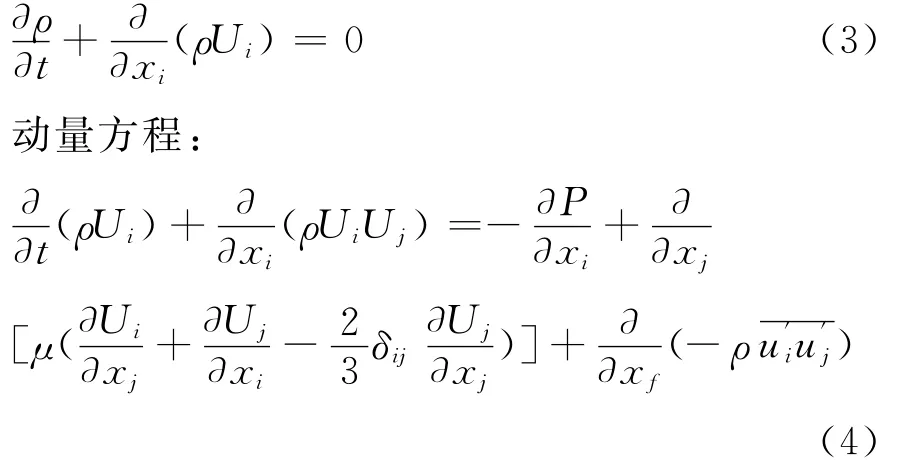
利用Boussinesq假设,把雷诺压力和平均速度梯度联系起来,湍流脉动所造成的切应力有:
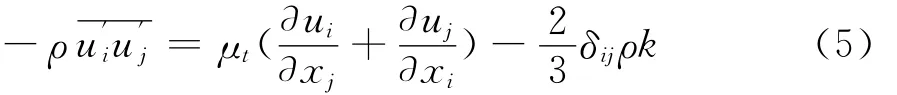
在此,将流体力学与热力学中的物理量做对应比较,见表1所示。
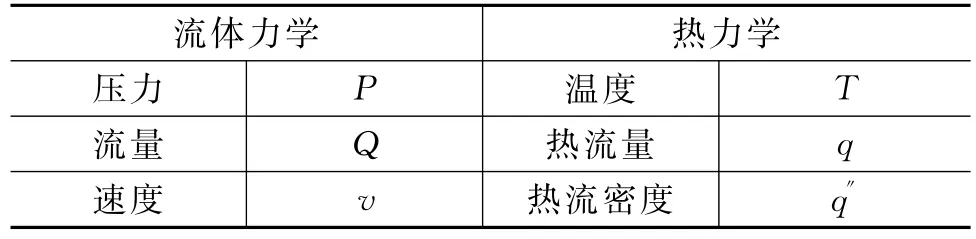
表1 流体力学与热力学物理量比较
在多孔介质中,如果稳定在一维状态下,不考虑流体的黏性,仅考虑热传导换热可以得到通式:

式(6)中,φ为驱动势(流体力学中的压力P,热力学中的温度T),θ为传导量(流体力学中的流量Q,热力学中的热流量q),δy、δz为单元尺寸,λ在热力学中为热导率,在流体力学中为阻力系数。
2.2 流场计算离散方法的选择
对各方程的离散采用经典的SIMPLE方法,其基本思想可描述为:
对于给定的压力场(可以是假定的值,或是上一次迭代计算所得到的结果),求解离散型式的动量方程,得出速度场。
因为压力场是假定的,或不精确的,这样,由此得到的速度场一般不满足连续方程,因此,必须对给定的压力场加以修正。修正的原则:与修正后的压力场相对应的速度场能满足这一迭代层次上的连续方程。
据此原则,把由动量方程的离散型式所规定的压力与速度的关系代入连续方程的离散形式,从而得到压力修正方程,由压力修正方程得出压力修正值。
根据修正后的压力场,得出新的速度场。然后检查速度场是否收敛。若不收敛,用修正后的压力值作为给定的压力场,开始下一层的计算。
如此反复,直至获得收敛的解。
3 流场及热场模拟结果的比较
前面主要介绍了求解流场的理论方法和编程思路,在实际应用中,常通过某些大型的CFD软件求解。现采用ANSYS10.0软件,对2种模型进行模拟计算和结果比较。
3.1 求解模型
在图1中,这是个二维多孔介质模型,左端和右端分别是流体的进口和出口,上端和下端为壁面,流体不能通过,多孔介质中间有2个圆柱形的实体,流体不能进入。
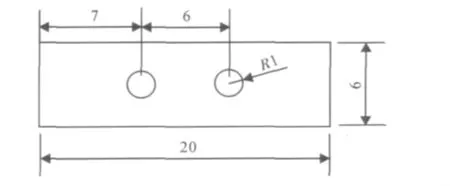
图1 二维多孔介质模型图
假定流场为层流,多孔介质各向同性,各参数设定如下:

3.2 模型网格的划分
在Ansys10.0软件中建立物理模型,经处理后,可得图2所示的计算网格。

图2 模型网格
3.3 计算结果对比及分析
在ANSYS10.0软件中,利用上述网格代入3.1节中所示的边界条件进行计算,迭代计算60步的误差分布,见图3所示。
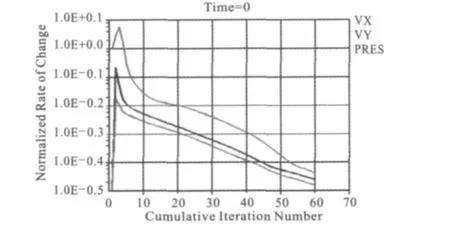
图3 迭代收敛图
由图3可知,在迭代过程中,整个计算结果是收敛的,最终误差也非常小。
在此,从比较两种分析方法所得的流场、热场分布图的角度,分析采用热力学模拟多孔介质流场的可行性。
当黏性值为μ=0.01 kg·m-1·s-1时,流体分析所得的流场分布,如图4所示。

图4 黏性值为μ=0.01 kg·m-1·s-1时的流场分布图
用热流密度模拟流场时,将左端进口的热流密度设为0.01 W·m-2,右端为等温边界条件,其余所有面都设为绝热条件。在此条件下,所得的热流密度分布如图5所示。
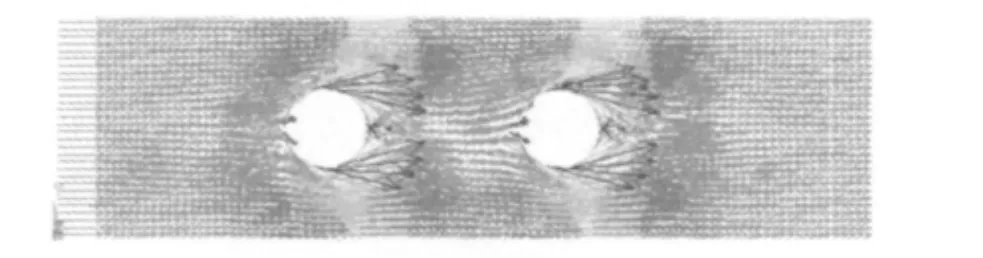
图5 热流密度模拟所得的流场分布图
对图4、图5的形态分析后,显然可发现两者之间的流场差别很大。热流密度模拟出来的流场较为平滑,而真实的流场高、低速区域相对集中。造成此现象的原因为:真实流场中的流体是有黏性的,而用热流密度模拟出来的流场没有考虑(也无法考虑)流体的黏性。
在真实流场中,不考虑黏性的影响(即μ=0 kg·m-1·s-1),此时得到的流场分布,如图6所示。通过比较图5、图6,可以发现,此时,两流场分布几乎完全一样。在实验过程中,逐渐减小流体的黏性值,真实流场的分布就会以图4中的形态,向图6中显示的状态逼近。
由此分析,可得结论:用热流密度的分布来模拟多孔介质内的流场分布是具有可行性的。
当流体为无黏性流体时,热流密度模拟的结果和真实结果相一致。当流体为黏性流体且黏性很大时,此模拟的误差较大。
当流体黏性不大时,可用热流密度近似模拟多孔介质流场的分布。
当流体无黏性时,根据能量守恒方程和质量守恒方程,可将热流密度对应于流体的速度,温度对应于流体的压强,同时,改变相应系数,不难发现,此时两种方法得出同一结论。即,它们的流场分布完全一样。
4 结 语
通过分析比较,讨论了用热学中热流密度这个参量来模拟多孔介质中流场分布的问题,得出了“热流密度可以模拟黏性很小的流体流场分布”的结论。
在多孔介质的内部流场,可直接用流体力学模型进行模拟。现采用的多孔介质模型,大多是在各向同性的假定下使用的。实际上,多孔介质不可能是各向同性的,在不同位置的孔隙率,粒子直径均有不同。综合考虑这些因素,在建模过程中,对材料不同位置导热率的设定,显然比多孔介质中不同位置的孔隙率等参数的设定要简单得多。在复杂的多孔介质中,用热模拟法来模拟流场的分布是具有优势的。
热流密度模拟法的不足之处,在于不能模拟黏性较大的流体的流场,只能模拟近似无黏性流体的流场,这也是此种模拟法的局限性所在。在水利工程方面,大多考虑的是土壤渗流和压强、时间的关系,不太在意流体的黏性,所以,此方法有较强的用武之地。
现在所讨论的实例较为简单,在真实复杂的三维瞬态模型中,流体力学与热力学中各参量对应的线性关系,需要根据实际情况确定。在复杂工况下,这两种方法的模拟结果存有哪些方面的差异,还有待于进一步研究。
[1]李萼,王康,张仁铎,盛丰.多孔介质中非均匀流活动性流场模型本构关系研究[J].水利学报,2008(2):151-157.
[2]SRINATH V.EKKAD and JE-CHIN HAN.Detailed heat transfer distributions in two-pass square channels with rib turbulators[J].Inr.J.Heat Mass Transfer.1997.40(11):2525-2537.
[3]Wnag K,Zhang R,Yasuda H.Characterizing heterogeneity of soil water flow by dye infiltration experiments[J].Journal of Hydrology,2006,328:559-571.
[4]Chen Wei,Liu Wei.Numerical and experimental analysis of convection heat transfer in passive solar heating room with greenhouse and heat storage[J].Solar Energy,2004,76(5):623-633.
[5]解茂昭.一种新概念内燃机//基于多孔介质燃烧技术的超绝热发动机[J].热科学与技术,2003(2):189-194.
[6]Bergles,A.E.Heat Transfer Enhancement—The Encouragement and Accommodation of High Heat Fluxes,ASME[J].Heat Transfer,1997,119:8-19.
[7]Chyou,Y.P.,Investigation of Fluid Dynamic Characteristics of Longitudinal Vortices[J].Trans.Aeronaut.Astronaut.Soc.ROC,1997,29(4):375-387.
[8]Liou,T.M.,Chen,C.C.LDV Study of Developing Flows Through a Smooth Duct with 180 Deg Straight-Corner Turn.ASME[J].Turbomach,1999(121):167-174.
[9]H H Macedo,U M S Costa,M P Almeida.Turbulent Effects on Fluid Flow through Discordered Porous Media[J].Physica AStatistical and Theoretial Physics,2001,299(3/4):371-377.
[10]King M S.Rock-physics developments in seismic exploration:A personal 50-year perspective[J].Geophysics,2005,70(6).
[11]高慧梅,姜汉桥,陈民锋.多孔介质空隙网络模型的应用现状[J].大庆石油地质与开发,2007(4):74-79.
The Method of Thermal Simulation in Flow Field with Porous Media
ZHANG Ming-bao
(Harbin Boiler Company Limited,Harbin,Heilongjiang 150046,China)
Along with the development of the energy industry rapidly,a quickly efficient cooling technology of porous media has become a hot topic in the fields of the engineering &heat exchange.In the performance research of porous media,we should not only pay attention to the capability of heat dissipation in macroscopic view,but also the effect inside of the flow field in microcosmic view.The numerical simulation of the flow distribution in porous media is not too much difficulty now,the method of hydrodynamics and thermal simulation instead of flow field in porous media is discussed mainly in this paper.It is not an advantageous method in a simple model,but it can simplify the model in the complicated condition of the porous media and the boundary condition,and save much time in modeling.
porous media;flow field;calculation;thermal simulation;heat exchange;value;model;method
TK262
A
1672-0210(2012)02-0009-04
2012-04-16
张明宝(1979-),男,工程师,大学本科,毕业于吉林化工学院,从事电站辅机设备及压力容器的设计开发工作。
简讯
