关于一类纯指数Diophantine方程

管训贵

（泰州师范高等专科学校数理信息学院，江苏 泰州225300）

1 引 言

设a，b，c是给定的正整数。方程

是一类基本而又重要的指数Diophantine方程。由于该方程的求解与著名的广义Fermat猜想有关，所以这是一个十分困难的问题。

1933年，K．Mahler运用p－adic形式的Thue－Siegel定理证明了：方程 （1）仅有有限多组正整数解（x，y，z）。1940年，A．O．Gel’fond 进一步给出方程 （1）的解数的可有效计算的上界。2001年，N．Terai［1］运用文献 ［2］中有关Pell的基本解与Bernoulli数的整除性之间的关系证明了：如果a，b，c满足a＋b＝c2，其中b是适合b≡5（mod12）的奇素数，c是适合c≡－1（mod b2）的奇数；或a＋b3＝c2，其中b是适合b≡5（mod12）的奇素数，c是适合c≡－1（mod b4）的奇数，则当Bernoulli数B（b－1）／2不能被b整除时，方程 （1）仅有正整数解分别为 （x，y，z）＝ （1，1，2）与 （1，3，2）。然而该结果的证明是错误的。2006年，乐茂华［3］去掉 “b是奇素数”、“Bernoulli数B（b－1）／2不能被b整除”等限制条件，证明了：如果a，b，c满足a＋b2l－1＝c2，b≡5（mod24），c是适合c≡－1（mod b2l）的奇数，其中l是任意正整数，则方程 （1）仅有正整数解 （x，y，z）＝ （1，2l－1，2）。

作为文献 ［3］的补充，本文运用初等数论方法证明了以下结果：

定理 如果a，b，c满足a＋b2l－1＝c2，b≡23（mod24），c是适合c≡－1（mod b2l）的奇数，其中l是任意正整数，则方程 （1）仅有正整数解 （x，y，z）＝ （1，2l－1，2）。

2 关键性引理

引理［4］如果a，b，c满足a＋b2l－1＝c2，b≡23（mod24），c是适合c≡－1（mod b2l）的奇数，其中l是任意正整数，则方程 （1）的正整数解 （x，y，z）适合2■y，2∣z。

证明 设 （x，y，z）是方程 （1）的一组正整数解。由c≡－1（mod b）及a＋b2l－1＝c2知，a≡1（mod b），此时

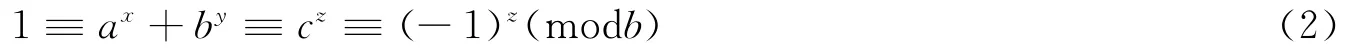
由于b是大于1的奇数，故 （2）式说明2∣z。

又因b≡－1（mod 3），故由a＋b2l－1＝c2知：当c≡0（mod3）时，a≡c2－b2l－1≡1（mod 3），即

当c≢0（mod3）时，a≡c2－b2l－1≡－1（mod 3），即

假定2∣y，则由方程 （1）可知，当c≡0（mod3）时，

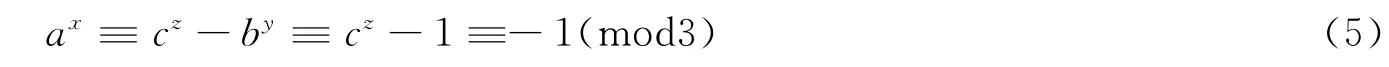
当c≢0（mod3）时，

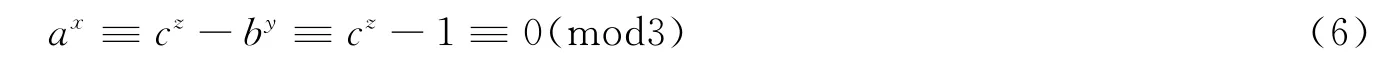
因为 （5）与 （3）、（6）与 （4）矛盾，所以2■y。至此本引理的结论已证明。

3 定理的证明

设（x，y，z）是方程 （1）的一组正整数解。根据本文的引理知y是奇数，z是偶数。因为b≡－1（mod8），故a≡c2－b2l－1≡1－（－1）≡2（mod8），即

又由方程 （1）可得

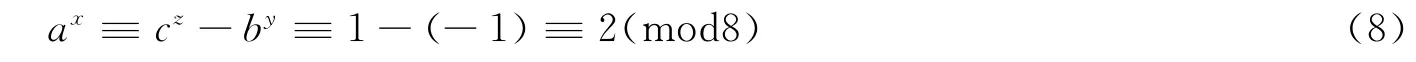
结合 （7）与 （8）立得x＝1。

由于x＝1，假定z＞2，则由方程 （1）及a＋b2l－1＝c2知，y＞2l－1，即y≥2l。另外，由c≡－1（mod b2l可得

同时，由方程 （1）可得

（10）与 （9）矛盾，说明z＝2，因此y＝2l－1。综上所述，如果a，b，c满足a＋b2l－1＝c2，b≡23（mod24），c是适合c≡－1（mod b2l）的奇数，其中l是任意正整数，则方程（1）仅有正整数解（x，y，z）＝（1，2l－1，2）。定理得证。

根据定理直接可得以下推论。

推论1［5］Diophantine方程

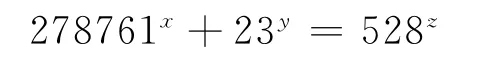
仅有正整数解 （x，y，z）＝ （1，1，2）。

推论2［6］Diophantine方程

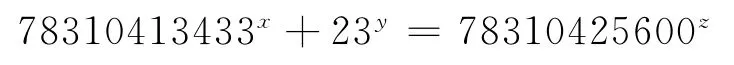
仅有正整数解 （x，y，z）＝ （1，3，2）。

［1］ Terai N．On the exponential Diophantine equation ax＋by＝cz［J］．Proc Japan Acad，2001，77A （08）：151－154．

［2］ Adachi N．The Diophantine equations x2＋ly2＝zlconnected with Fermat’s last theorem ［J］．Tokyo J Math，1988，11 （01）：85－94．

［3］ 乐茂华．关于三项纯指数Diophantine方程的一点注记 ［J］．湖北民族学院学报：自然科学版：2006，24（03）：209－210．

［4］ 管训贵．不定方程x2－py2＝z2的正整数解 ［J］．河北北方学院学报：自然科学版，2009，2（05）：5－7．

［5］ 管训贵．关于不定方程x2＋（p－1）y2＝pz2［J］．河北北方学院学报：自然科学版，2011，26（01）：12－14．

［6］ 管训贵．初等数论 ［M］．安徽：中国科学技术大学出版社，2011：3－10．