超临界二氧化碳水平管内层流混合对流换热数值模拟
杨传勇 徐进良 王晓东 张 伟
(1新能源电力系统国家重点实验室 北京 102206)(2能源的安全与清洁利用北京市重点实验室 北京 102206)(3华北电力大学低品位能源多相流与传热北京市重点实验室 北京 102206)
1 引言
超临界流体由于其特殊的热物理性质被广泛应用于超临界萃取、火箭和航天器的冷却、空调和热泵系统等。由于CO2无毒、不可燃,化学性质非常稳定,且臭氧消耗潜能ODP=0、全球变暖潜能GWP=1,对环境具有友好性,因此开始受到人们更多重视。超临界流体在微通道中的应用较多,如汽车空调采用跨临界CO2制冷系统时,其气体冷却器要做成直径小于1 mm的微通道管[1],于是对超临界流体在微细管道内基于其物性变化、浮升力等诸多因素对对流换热的影响做出研究是非常有必要的。
Liao 等[2-3]对超临界 CO2在水平和竖直微细圆管内换热做了实验和数值模拟,分析了管径0.5—2.16 mm的管道传热系数和Nu数随着主流温度的变化,得到流体雷诺数Re高达105时管内的浮升力作用仍不可以忽略。张丽娜[4]、曹侃[5]等也对超临界CO2在管内换热进行了数值研究。因实验条件的限制对微细管内的二次流研究较少,于是对超临界CO2管内换热时浮升力引发的二次流及其强化换热的机理仍需要开展更深入的研究。本文通过数值计算对管内因浮升力引发的二次流进行定量分析,发现浮升力对管内换热具有强化作用,分析了重力水平、壁面温度、入口Rein等对流动和换热的影响,可以为设计新型高效紧凑的换热器提供理论依据。
2 物理模型和数学模型
2.1 物理模型
选用的物理模型及坐标系统如图1所示,管道直径d=0.5 mm,长L=1 000 mm,壁面采用恒壁温冷却。在水平管中,重力引发的浮升力会引起二次流,所以管道壁面参数沿周向角度θ的分布是不同的,其中管道的上母线和下母线分别对应周向角度90°和-90°。文中所有工况均采用Fluent软件计算,模型采用变物性,不同温度和压力下超临界CO2的热物性参数通过NIST网站获得,软件中CO2的热物性参数按照piecewise-liner方法输入。压力和速度耦合采用SIMPLEC算法,动量和能量方程采用二阶迎风格式的差分方法,采用质量入口和自由出流边界条件,壁面温度设为T=Tw,且采用无滑移壁面边界条件。为了消除网格密度对计算结果的影响,通过对逐渐加密的网格进行计算得到近似的网格无关解。
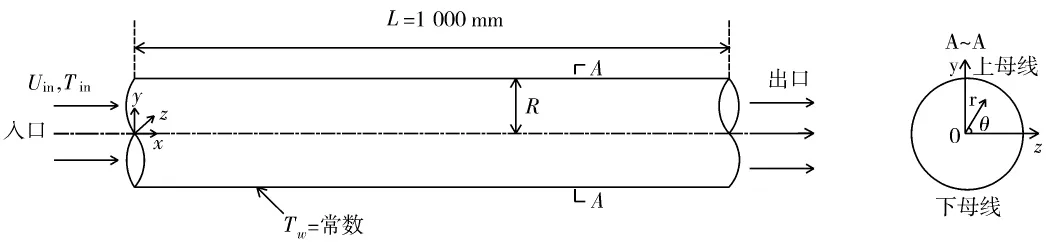
图1 物理模型及坐标系统Fig.1 Physical model and coordinate system
2.2 数学模型
水平管中流体因浮升力的影响会产生分层现象,于是本文采用三维模型计算更接近实际。连续方程、动量方程、能量方程可参见文献[1],动量方程考虑重力加速度g’的变化,其中g=9.81 m/s2,文中所有参数均取国际单位。
主流的截面平均温度Tb为:
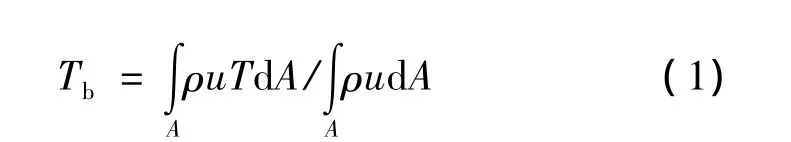
通过管道壁面的热流量qw为:

壁面的局部传热系数h为:

壁面的局部努塞尔数为:

通过引入相对二次流动能将二次流大小定量的表示出来。K定义为:
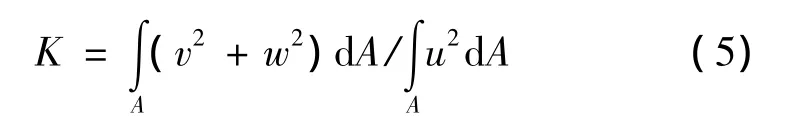
局部范宁摩擦系数Cf为:

其中:τw为壁面剪切力,由牛顿粘性定律公式来求:由于Cf的值比较小难以区分,因此选用Cf×Reb来代替Cf,其中截面平均Reb数定义为:

式中:u、v、w 分别对应 x、y、z三个方向的速度;d为管道直径;λ为导热系数;ρ为流体密度;μ为动力粘度;下标b为取截面平均;A为管道横截面积;w为壁面;g’为重力加速度;Tb为截面平均温度;qw为热流量,W/m2;h为传热系数,W/(m2·K)。
3 数值模拟结果及分析
3.1 模型验证
压力为8 MPa时,超临界CO2的cp、λ、μ和ρ随T的变化如图2所示。8 MPa时超临界CO2在307.6 K时cp达到峰值,这个峰值点就是超临界CO2在8 MPa时对应的拟临界点,此点的温度即为拟临界温度。在拟临界点附近超临界CO2的物性变化最为显著,特别是cp和ρ的值变化很大,而拟临界点附近以外的区域物性随温度的变化很小。

图2 8.0 MPa时CO2的热物性参数随温度变化Fig.2 Thermophysical properties of CO2at 8.0 MPa
为验证模型的正确性,首先对文献[1]中的工况进行计算,其中超临界CO2压力为8 MPa,质量流量m=1.6 ×10-5kg/s,壁面温度 Tw=298.15 K,入口温度Tin=393.15 K,将计算得到的不同位置处壁面局部Nu数随周向角θ的变化与文献[1]中的数据对比,如图3所示。通过对比可以发现周向角度θ从-90°到0°时模拟与文献结果基本相同,当θ>0°时Nu的值有些偏差,但总的来说模拟与文献结果相差不大,且两者的变化趋势是相同的,于是本模拟所建模型是可靠的,可以得到超临界CO2在管内流动的换热特征。
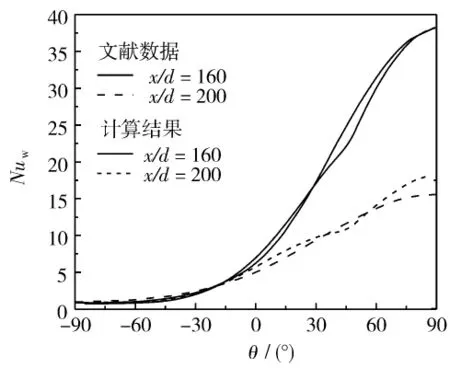
图3 模拟结果与文献对比Fig.3 Comparison between simulation and literature data
3.2 局部传热系数
图4为改变壁面温度时上下母线的传热系数随x/d的变化规律,其中重力加速度取g’=1 g,Tin=393.15 K,m=1.6×10-5kg/s。图中上母线的传热系数明显高于下母线,上母线传热系数先增加到峰值,跨过峰值之后传热系数迅速降低。由于冷却时近壁面流体温度低、密度大,中心流体温度高、密度小,密度差产生浮升力使得近壁面处流体向下运动,而中间温度较高的流体向上运动,于是在管道横截面上产生二次环流,增强了壁面处的换热。二次流使传热能力强的流体聚集在上母线处,而传热能力较差的流体分布在下母线处,于是上母线传热系数高于下母线。当流体处在拟临界温度附近区域时,比热容会达到很大值,密度变化也非常大,此时引起的浮升力最强烈,使得在该区域传热系数达到峰值。壁面温度越低上母线传热系数峰值越大,这主要是由于冷壁面温度越低主流和壁面之间的温差越大,引起的二次流越强,使传热系数越大。跨过拟临界温度区域后壁面温度越高上母线的传热系数越大。

图4 壁面温度对上下母线h随x/d变化的影响Fig.4 Effect of wall temperature on variation of top and bottom generatrix heat transfer coefficient with x/d
图5所示的是改变重力加速度g’时上下母线的传热系数随Tb的变化规律,其中 Tw=298.15 K,Tin=393.15 K,m=1.6 ×10-5kg/s。由图 4、图 5 可见,在管道的入口处因入口效应传热系数均是先降低后升高,因为入口处温度梯度较大,边界层很薄,使传热系数较大。图中重力加速度为零时上下母线传热系数相同,重力加速度不为零时,上母线传热系数高于下母线,随着重力加速度的增加上母线的传热系数逐渐增加。重力加速度越大流体分层越明显,管内上、下部分流体的温差越大,二次流越强,使传热系数增加。传热系数在拟临界温度区域达到峰值,且重力加速度为零时传热系数在拟临界温度附近区域也存在一个峰值,这均是由超临界CO2热物性的巨大变化所引起的。
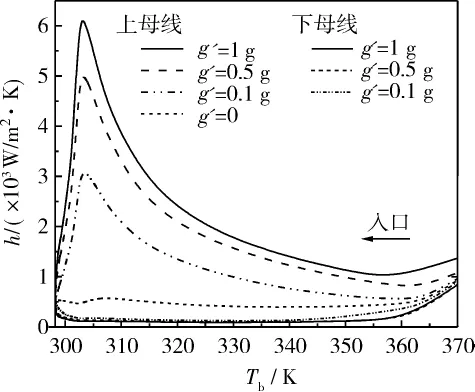
图5 重力水平g’对上下母线h随Tb变化的影响Fig.5 Effect of gravity acceleration on variation of top and bottom generatrix heat transfer coefficient with Tb
3.3 管内二次流变化
图6给出的是改变入口Rein数时K随x/d的变化规律,其中Tw=298.15 K,g’=1 g,Tin=393.15 K。随着入口Rein数的增加K是逐渐减小的,因为入口Rein数越大对应的质量流量越大,浮升力引发的二次流较大,但是轴向速度增加的更多,惯性力更强,使得K越小,K在靠近入口达到峰值,跨过峰值后K有一个极值点,因为此点处在拟临界点附近,物性变化剧烈,二次流较强。K最终趋于零,主要是由于流体已经接近充分发展,流体之间的温差很小使得密度差很小,于是浮升力引发的二次流几乎为零。
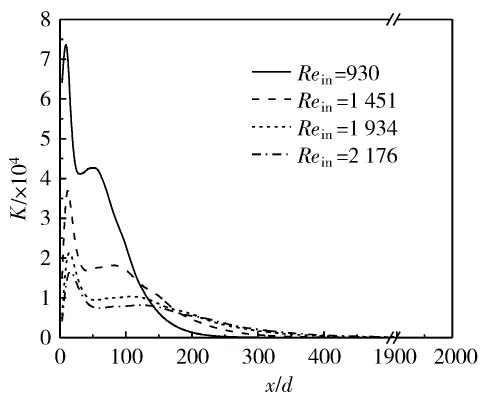
图6 入口Rein数对K随x/d变化的影响Fig.6 Effect of Reinnumber on variation of K with x/d
图7所示的是改变壁面温度时K随x/d的变化关系,其中 g’=1 g,Tin=393.15 K,m=1.6 ×10-5kg/s。可见在靠近管道入口处出现K峰值,在未达到峰值前随着冷壁面温度的降低K是逐渐升高的,壁面温度越低K更快的趋于零,因为在没有达到峰值前,壁面温度越低,壁面与流体之间的温差越大,最终引发的二次流越大,K越大。当到达峰值后,冷壁面温度越低管内二次流越小,K越小。
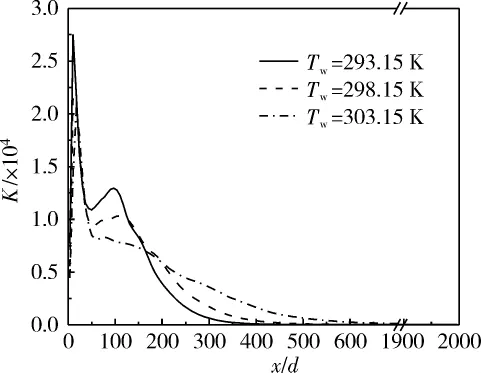
图7 冷壁面温度对K随x/d变化的影响Fig.7 Effect of wall temperature on variation of K with x/d
图8中所示的是改变重力加速度g’时K随x/d的变化规律,其中 Tw=298.15 K,Tin=393.15 K,m=1.6×10-5kg/s。K先增加到峰值然后减小到趋于零,且在靠近管道入口处达到峰值。随着重力加速度的增加K也增大,因为重力加速度越大浮升力越大,产生的二次流越强。重力加速度为零时K在靠近入口处就降到了零,因零重力时不会产生浮升力,也就不会有二次流。零重力时二次流趋于零,不会增强传热,表现为图5中零重力时上母线传热系数远低于有重力时。图6—图8中可见,K均是在管道入口处较大,与文献[6]结果相同,因为入口处温度梯度大,物性变化剧烈,浮升力大,二次流强,于是K较大。
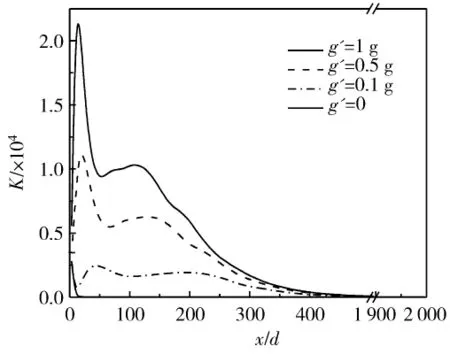
图8 重力水平g’对K随x/d变化的影响Fig.8 Effect of gravity acceleration on variation of K with x/d
3.4 局部范宁摩擦系数
图9给出的是不同入口Rein数时上下母线的Cf×Reb随x/d的变化规律,其中Tw=298.15 K,g’=1 g,Tin=393.15 K。靠近入口处上母线的 Cf×Reb先升高到峰值后迅速降低,最后趋于恒定值,且上母线的Cf×Reb高于下母线,下母线的Cf×Reb在靠近入口处就从最大值降到很低,然后产生范围不大波动,当流体接近充分发展后上下母线的Cf×Reb维持16不变,这与文献[1]的结果是一致的。因为浮升力的作用使得上母线处流体的温差大于下母线,于是靠近上母线处流体的物性变化要强于下母线,当流体接近充分发展时,温差几乎不变,流体的物性参数不再变化,接近为常物性参数流动,于是上下母线的Cf×Reb维持16不变。随着入口Rein数的增加Cf×Reb的峰值变化不大,但是出现峰值的位置要靠后,主要是由于物性剧烈变化的位置随Rein数的增加而靠后。

图9 入口Rein数对Cf×Reb随x/d变化的影响Fig.9 Effect of Reinnumber on variation of Cf×Rebwith x/d
图10给出的是不同壁面温度时上下母线的Cf×Reb随x/d的变化规律,其中 g’=1 g,Tin=393.15 K,m=1.6×10-5kg/s。上母线 Cf×Reb的峰值随冷壁面温度的降低而增大,因为壁面温度越低时拟临界区域物性变化越剧烈,浮升力越大,进而引起的壁面剪切力越大。冷壁面温度越低,Cf×Reb达到峰值的位置越靠近管道入口,最终上下母线的Cf×Reb的值收敛于16。

图10 冷壁面温度对Cf×Reb随x/d变化的影响Fig.10 Effect of wall temperature on variation of Cf×Rebwith x/d
图11给出的是改变重力加速度g’时上下母线的Cf×Reb随x/d的变化规律,其中Tw=298.15 K,Tin=393.15 K,m=1.6 ×10-5kg/s。零重力时上下母线的Cf×Reb是相同的。有重力加速度时靠近入口处上母线的Cf×Reb明显高于下母线,下母线的Cf×Reb低于零重力时,这是因为在有重力时靠近下母线处的流体的物性变化相对较小,使得壁面剪切力较小,从而下母线的Cf×Reb也较小。随着重力加速度的减小上母线Cf×Reb的峰值是减小的,因为重力加速度越小管内流体的温差越小,物性变化不再剧烈,峰值减小。下母线的Cf×Reb在有重力时相差不大。图9—图11可见,由于入口效应Cf×Reb在入口处均是先降低后增加,这是因为入口处速度梯度比较大,使剪切力较大,Cf×Reb较高。
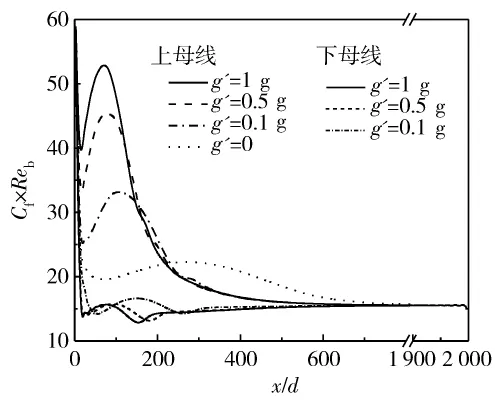
图11 重力水平g’对Cf×Reb随x/d变化的影响Fig.11 Effect of g’on variation of Cf×Rebwith x/d
4 结论
对超临界CO2在长1 000 mm,管径0.5 mm的水平圆管内层流混合对流换热做了数值模拟,分析了入口Rein、冷壁面温度及重力水平对管道内换热的影响,有如下结论:
(1)因入口效应管道上母线的传热系数在靠近入口处先降低后升高,在拟临界温度附近区域达到峰值,上母线的传热系数要远大于下母线。冷壁面温度越低上母线传热系数峰值越大。重力加速度越大管内传热系数越大,零重力时管道上母线传热系数要远低于有重力加速度时。
(2)K均在入口处达到最大,且流体在管内充分发展时均趋于零。入口Rein数越大K越小,冷壁面温度越低时K的峰值越大,重力加速度越大K越大,重力加速度为零时K为零。
(3)Cf×Reb在入口处因入口效应先降低后增加,上母线的Cf×Reb先增加后减小且在靠近入口处远大于下母线,下母线的Cf×Reb在入口处就降到很低而后产生波动,最后二者都收敛于16,这与常物性的流动换热是一致的。入口Rein数变化时Cf×Reb的峰值变化不大,冷壁面温度越低或重力加速度越大时,上母线Cf×Reb的峰值越大。
1 Cao X L,Rao Z H,Liao S M.Laminar convective heat transfer of supercritical CO2in horizontal miniature circular and triangular tubes[J].Applied Thermal Engineering,2011,31:2374-2384.
2 Liao S M,Zhao T S.A numerical investigation of laminar convection of supercritical carbon dioxide in vertical mini/micro tubes[J].Progress in Computational Fluid Dynamics,2002(2):144-152.
3 Liao S M,Zhao T S.An experimental investigation of convection heat transfer to supercritical carbon dioxide in miniature tubes[J].2002,45:5025-5034.
4 张丽娜,刘敏珊,董其伍,等.超临界二氧化碳微细管内冷却换热研究[J].低温工程,2010(1):38-42.
5 曹 侃,董其伍,刘敏珊,等.超临界CO2冷却换热特性数值模拟[J].低温工程,2012(1):56-60.
6 徐 峰,郭烈锦,白博峰.管内超临界压力水的混合对流换热[J].工程热物理学报,2005,26(1):76-80.

