爆炸荷载下网壳结构的动力响应及泄爆措施*

翟希梅，王永辉

(哈尔滨工业大学土木工程学院，黑龙江 哈尔滨150090)

目前，全世界每年发生恐怖爆炸袭击事件及突发爆炸多达数百起，对于人群集中的大跨度体育场馆，发生爆炸的后果更严重、受恐怖爆炸袭击的潜在可能性也更大，因此，迫切需要对此类重要建筑在爆炸荷载下的响应规律及其防御措施进行研究。目前，对于结构爆炸响应的研究主要集中在结构构件与节点、混凝土框架或钢框架结构上［1-8］，对于承受爆炸荷载的大跨度空间结构研究极少，这种现状与作为公共建筑的大跨度网壳结构所面临的严峻安全威胁相比严重滞后。

本文中，利用ANSYS/LS-DYNA 软件建立中心TNT 爆炸荷载作用下40 m 跨度的K8 型单层球面网壳的精细化有限元模型，利用多物质ALE 算法模拟爆炸冲击波在空气中的传播，采用流固耦合算法模拟爆炸冲击波与结构的相互作用，分析屋面板开洞率、开洞数量、洞口分布等对结构响应的影响。

1 有限元模型建立及参数选取

1.1 炸药和空气模型

大跨度网壳结构形成的空间巨大，因此当炸药位于结构中心时，考虑整体模型的对称性，以炸药为中心取1/4 模型进行模拟，简化后空气域范围为20.4 m(长)×20.4 m(宽)×19.8 m(高)，空气和炸药的有限元模型如图1 所示。炸药和空气单元类型采用8 节点的Solid 164 单元，每个节点具有9 个自由度，分别是3 个方向的位移、速度和加速度。炸药和空气采用ALE(arbitrary Lagrange-Euler)算法［9］，此算法结合了Lagrange 算法和Euler 算法的优点，克服了固体大变形引起的有限元网格严重畸变问题，更适合模拟爆炸冲击波在空气中的传播。

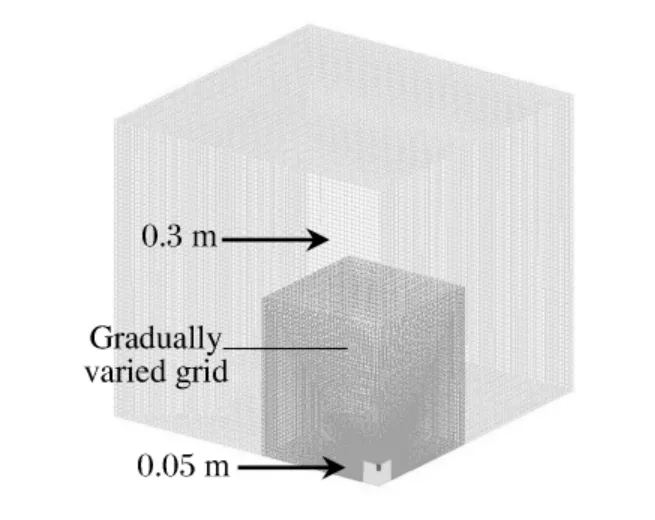
图1 空气和炸药有限元模型Fig.1 Finite element of air and explosive

由于冲击波峰值超压随比例距离的增加而迅速降低［10-11］，因此在进行网格划分时采用渐变网格划分方式(见图1)，在比例距离较小的地方网格较细(0.05 m)，随着比例距离的增加，空气网格尺寸越来越大，到一定比例距离后保持不变(0.3 m)。本文中采用的渐变网格划分方式既可以使峰值超压在急剧变化的地方满足精度，又可大大减少单元数量，进而减少计算时间。

文献［12］中对爆炸冲击波在自由空气域中的传播规律进行了研究，并提取了峰值超压的有限元计算结果，将该结果与多个经验公式进行对比，验证了本文中关于空气与炸药的材料模型、状态方程、渐变网格形式及尺寸、1/4 模型应用的有效性和适用性。

1.2 网壳模型

由于TNT 炸药位于网壳结构的中心，为减少计算量，建立了跨度40 m 的K8 型单层球面网壳结构的1/4 有限元模型，如图2所示。此外，考虑爆炸对网壳结构的最不利影响，在数值模拟中将地面和网壳下的10 m 高的墙体设置为刚性材料。根据实际网壳结构的典型构造进行了较为精细化的模型建立:网壳的主杆、纬杆和斜杆均采用Ø 114 mm×4.0 mm 钢管;檩托采用Ø 76 mm×4.0 mm 钢管。实际工程中，檩条的截面通常是槽型截面，为建模方便，将檩条按刚度相等原则等效为空心矩形截面。檩条与屋面板(钢板)之间通过直径12 mm 的铆钉相连，且每一根檩条上均匀设置7 个铆钉。网壳结构的屋面板是由压型钢板和保温材料组成的，由于保温材料的刚度和强度相对钢材来说均很低，为使问题简化，在计算中没有考虑保温材料的影响，按平面钢板建立了屋面板模型。1/4 网壳模型的网壳杆件与上部檩条具有相同的平面分布，两者通过0.2 m 高的檩托相连，屋面板布置于檩条上，并通过铆钉相连。网壳杆件、檩托、檩条和铆钉采用Beam 161 单元，该单元考虑了横向剪切应变的影响;屋面板、墙体和地面采用Shell 163 单元;1.2 kN/m2的均布屋面荷载通过质量单元加到网壳结构节点上，质量单元采用Mass 166。

本文中选择多段线性塑性模型9］。该模型可以根据实际情况，自定义有效真应力与有效塑性应变，以及应变率对屈服应力影响的比例因子，材料模型如下

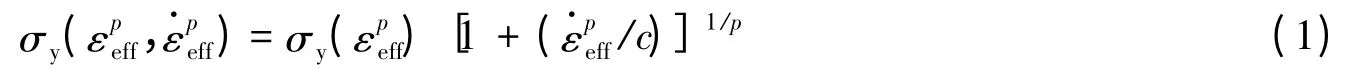
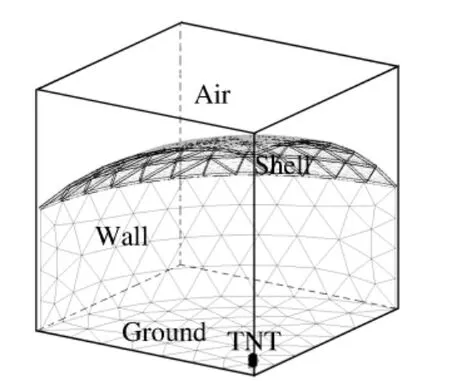
图2 结构有限元模型Fig.2 Finite element of the structure

2 结构动力响应参数分析

2.1 矢跨比影响

选择3 种典型的矢跨比S/L 进行分析，分别是1/4、1/5 和1/7。3 种矢跨比下结构在104 kg 等效TNT(一个飞毛腿导弹的等效TNT 当量为120 kg)爆炸荷载作用下的动力响应如表1 所示，表中ε－p 表示平均塑性应变，y1，max表示节点1最大竖向位移。网壳杆件的环形截面上有4个积分点，为说明网壳杆件截面的塑性发展程度，定义1P 表示只有1 个积分点进入塑性，4P 则表示杆件全截面进入塑性。表1 结果显示:随矢跨比的减小，网壳杆件、檩条、檁托、屋面板的平均塑性应变(网壳结构各组成部分塑性应变的算术平均值)、铆钉的失效单元比例和网壳中1P 和4P 杆件的比例是增加的，说明随矢跨比的降低，网壳的动力响应逐渐增大，对结构抗爆不利。

表1 不同矢跨比下结构响应Table 1 Structural response for varied rise-span rates

不同矢跨比的结构在爆炸荷载下节点1(位于网壳中心顶点)的竖向位移y1随时间的变化过程如图3 所示。从图中曲线可知，竖向位移在爆炸的初始0.2 s 内首先急剧增加，达到最终变形位置，然后在一个相对平稳的范围内波动。矢跨比为1/7 的网壳的竖向位移最大，这是由于相对于其他矢跨比，此时网壳的竖向刚度最小，从而爆炸后的位移响应更显著。此外，矢跨比较大的网壳为爆炸冲击波的传播提供了更大的空间，使得作用到结构上的冲击波强度减弱。

2.2 炸点距离影响

设置了3 个TNT 炸点中心到地面的高度h，即1.2、1.4、8.4 m，TNT 药量为104 kg，矢跨比为1/5 的网壳结构在爆炸荷载下的动力响应如表2 所示。可以看出，随炸点位置的上升(即炸点到地面距离的增加)，网壳杆件、檩条、檩托、屋面板和铆钉的响应程度是增加的。从网壳杆件塑性发展程度看，网壳进入塑性杆件(1P)的比例在炸点距地面1.2 m 时最小，而其他几种情况的网壳进入塑性杆件的比例相同，都为90.0%。网壳杆件全截面进入塑性(4P)比例的规律和网壳平均塑性应变的规律是相同的，也是逐渐增加，在8.4 m 时达到最大值。可见，爆炸点与网壳结构的距离越近，结构的动力响应越大。

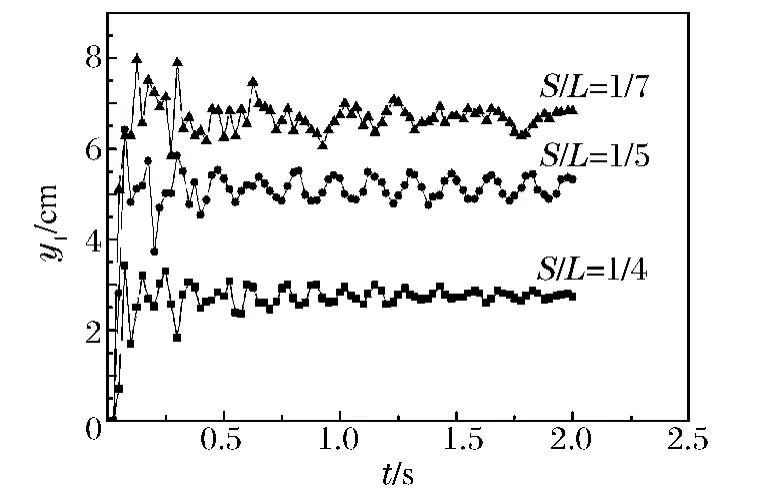
图3 不同矢跨比下节点1 竖向位移时程Fig.3 Vertical displacement-time curve of Node 1 for varied rise-span rates

3 种不同炸点距离下竖向位移如图4 所示，从图中可知:节点1 竖向位移都首先达到一个最大值，即网壳首先在较短时间内完成塑性变形，然后在塑性变形后形成的新平衡位置做小振幅的位移振荡。爆炸冲击波作用后，如果结构不再承受任何动荷载，节点1 最终将会在其波动的平衡位置静止，通过观察网壳节点1 塑性变形后振动的平衡位置可判断，炸点中心距地面8.4 m 情况下节点1 最终位移达到最大，1.2 m 情况下节点1 最终位移为最小。

2.3 屋面板厚度影响

屋面板在结构爆炸中是承受爆炸荷载的主要对象，且屋面板在承受爆炸荷载后将通过铆钉和檩托将荷载分别传递到檩条和网壳杆件上。本文中选择2 种典型的TNT 药量和3 种不同的屋面板厚度(1、2 和3 mm)分析不同屋面板厚度对结构响应的影响。

表3 给出了TNT 等效药量W=104、1 630 kg 时不同屋面板厚度δ 情况下结构的响应结果。可以看出，在104 kg TNT 炸药作用下，随着屋面板厚度的增加，网壳杆件、檩条、檩托和屋面板的塑性发展程度降低，并且铆钉的破坏程度也减轻。此外，网壳进入塑性的杆件(1P)比例和全截面进入塑性的杆件(4P)比例也逐渐减小。这主要是因为屋面板厚度的增加一方面使得屋面板在发生塑性应变时会消耗更多的能量，因此传递到其他部分的力就相对减小了;另一方面也使得屋面板的刚度增加而降低其变形。另外，随屋面板厚度的增加，节点1 的最大位移依次减小，这说明网壳的变形也是依次减小的。总之，在较小的TNT 药量情况下增加屋面板的厚度，可以减轻结构在爆炸荷载下的响应程度。

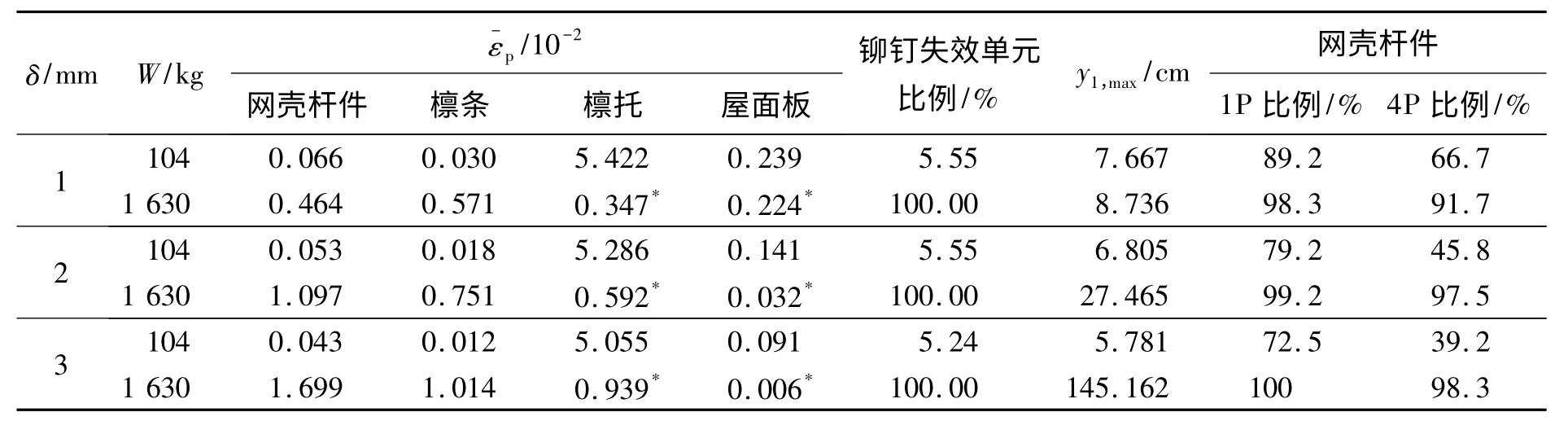
表3 不同屋面板厚度情况下结构响应统计Table 3 Structural response for varied thickness of roof boarding

在1 630 kg TNT 炸药作用下，结构的响应规律与104 kg 小炸药量下不同，具体表现为:随屋面板厚度的增加，网壳构件、檩条和檩托的响应程度增加了，且网壳杆件中进入1P 和4P 的比例也提高了，主要是因为在1 630 kg 这样的较大药量作用下，铆钉全部断裂，屋面板发生破坏，出现失效单元(见表3)，使得屋面成为泄爆途径，此时屋面板厚度增加，虽降低了屋面板本身的破坏程度(失效单元比例由22.4%降低到0.6%)，但屋面板泄爆能力被限制，使其他部分承受更大的荷载。因此，在这种情况下，增加屋面板厚度，将导致网壳、檩条和檩托的响应增大。通过观察网壳节点1 最大竖向位移可知，随屋面板厚度的增加，节点1 的最大位移依次增加，且当屋面板厚度为3 mm 时，y1，max远远大于其他两种情况。因此，屋面板的厚度对网壳结构的影响是与炸药量及屋面板是否发生破坏而成为泄爆口相关联的。

3 屋面板泄爆对网壳结构动力响应的影响

在爆炸发生时，冲击波荷载主要是通过与屋面板的相互耦合作用传到结构上的，因此，利用屋面板作为网壳结构在爆炸荷载下的泄爆途径，将起到很好的防御效果。

3.1 屋面板开洞率影响

根据K8 网壳的实际结构布置，在屋面板上均匀开设洞口，分析在TNT 药量为204 kg 的爆炸荷载作用下的结构响应，屋面板开洞率R 分别为0%、14%、25%、40%和50%，其洞口分布如图5 所示。

不同屋面板开洞率情况下的结构响应如表4 所示。从表中可知，随屋面板开洞率的增加，网壳构件、檩条、檩托和屋面板的塑性发展程度呈降低趋势。相对于未开洞的情况，开洞率为50%的网壳构件的平均塑性应变降低了89%，檩条降低了79%，檩托降低了72%，屋面板降低了15%，且网壳构件的1P 和4P 比例也明显降低。另外，网壳上节点1 处的最大竖向位移也呈现减小趋势。随着屋面板开洞率的增加，铆钉的破坏程度也逐渐减轻。

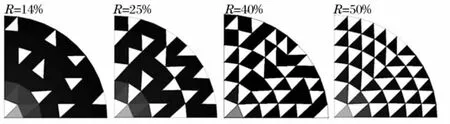
图5 屋面板开洞率分布图Fig.5 Distribution of opening rates on roof boarding

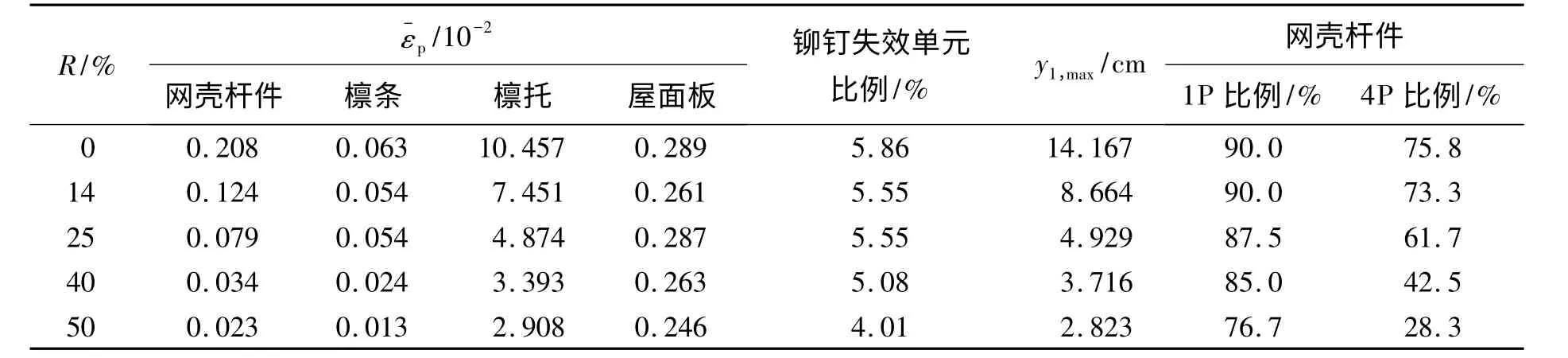
表4 不同屋面板开洞率情况下结构响应统计Table 4 Structural response for varied opening rates on roof boarding

不同开洞率情况下，网壳的塑性发展深度和分布情况如图6所示，图中杆件上的圆环代表该杆件塑性应变值，圆环越大塑性应变值越大;杆件上的数字代表杆件进入塑性的积分点个数。从图6 可知，随屋面板开洞率的增加，网壳杆件的塑性应变值明显降低，特别是处于6 环位置的杆件。此外，当屋面板开洞率增加时，各网壳杆件进入塑性的积分点的个数减少了，表明网壳的塑性发展程度总体呈下降趋势。上述的结构响应规律表明，随屋面板开洞率的增加，结构的动力响应程度降低，爆炸荷载对网壳的破坏作用减小。

3.2 屋面板开洞数量及洞口分布的影响

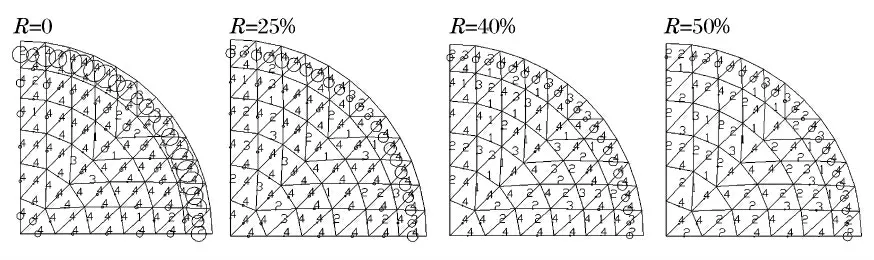
图6 网壳杆件塑性发展程度和深度Fig.6 Plastic development degree and distribution for reticulated shell members

为了解相同开洞率(R=50%)情况下，开洞数量及洞口分布对结构响应的影响，针对TNT 炸药当量为204 kg时分析了4 种不同开洞数量n 及洞口分布下的结构响应，洞口分布如图7 所示，结构的响应如表5 所示。

从表5 中可知，当屋面板开洞数量为1 时，网壳构件和屋面板的平均塑性应变最小，说明集中开洞时，对网壳构件和屋面板是有利的。而屋面板开洞数量为36 时，檩条的平均塑性应变最小，说明在相同的开洞率情况下，开洞数量越多、越均匀时，对檩条越有利。而当开洞数量为6 和12 时，檩托的平均塑性应变则相对较小。对于铆钉，当屋面板开洞数量为36时，其破坏程度最严重，这是因为在这种情况下参与工作的铆钉的数量最大，从而发生破坏的几率越高。随着屋面板开洞数量的增加，网壳杆件中进入塑性(1P)的比例和全截面进入塑性(4P)的比例是逐渐增加的。

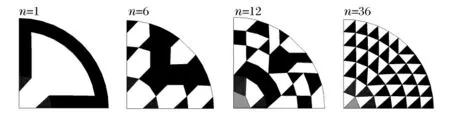
图7 屋面板开洞数量分布图Fig.7 Distribution of opening numbers on roof boarding

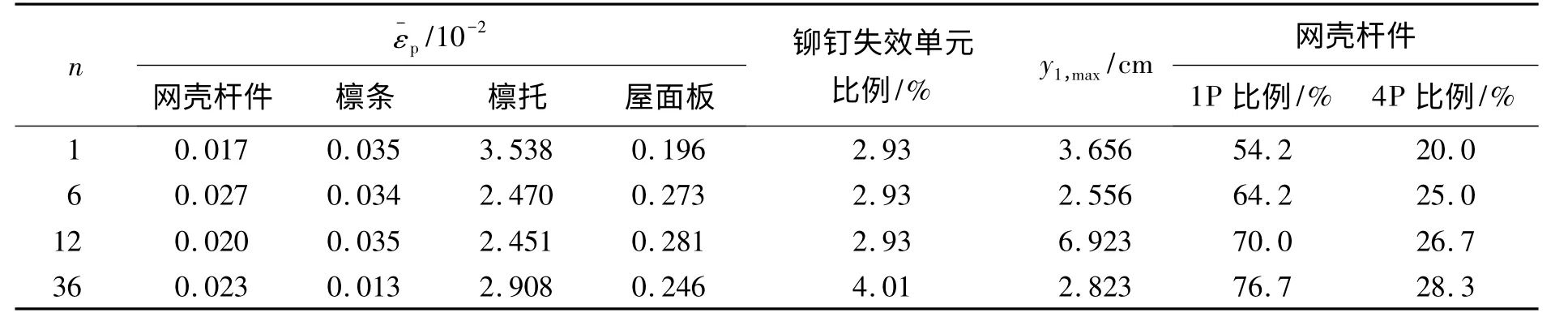
表5 不同屋面板开洞数量情况下结构响应统计Table 5 Structural response for varied opening numbers on roof boarding

3.3 屋面板开洞位置影响

在TNT 炸药当量204 kg、开洞率14%和开洞数量为1 的情况下，分析了3 种开洞位置下的结构响应，其开洞位置见图8，结构的响应如表6 所示。

由表6 可知，当屋面板开设的洞口处于位置I时，网壳构件、檩条和檩托的塑性发展程度最小，且网壳节点1 的最大竖向位移明显小于其他2 种情况，这主要是因为开洞位置位于结构的顶点，此处结构离炸点最近，最先接触爆炸冲击波，而且冲击波的峰值超压也最大，因此在此处开洞有利于直接泄掉爆炸荷载，降低网壳、檩条和檩托的动力响应。在3种不同开洞位置的情况下，屋面板的平均塑性应变值、铆钉的破坏程度很接近。当屋面板开设的洞口处于位置Ⅱ时，网壳总体的塑性发展程度最深，且网壳中1P 和4P 杆件的比例也最高。

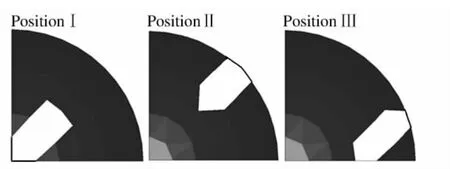
图8 屋面板开洞位置分布图Fig.8 Distributions of opening positions on roof boarding

表6 不同屋面板开洞位置情况下结构响应统计Table 6 Structural response for varied opening positions on roof boarding

4 结 论

(1)建立的大跨度空间网壳爆炸计算有限元模型，参数选取适当，可应用于网壳结构在爆炸作用下的结构动力响应分析。(2)相同爆炸荷载下，增加结构矢跨比可以减小结构的动力响应程度。爆炸点与结构距离越小，冲击波压力场强度越大，导致结构的响应程度增加。(3)TNT 炸药当量较小时，随着屋面板厚度的增加，结构动力响应程度降低;TNT 炸药当量较大时，会造成屋面板的破坏而成为泄爆途径，此时增加屋面板厚度，会加大网壳杆件、檩条和檩托的响应程度。因此屋面板厚度对网壳结构的影响与炸药量及屋面板是否破坏成为泄爆途径相关。(4)在屋面板开设洞口可有效减少结构动力响应，起到泄爆作用。屋面板集中开洞可提高爆炸冲击波的泄压效果，从而减小爆炸对网壳和屋面板的破坏。

［1］ Luccioni B M，Ambrosini R D，Danesi R F.Analysis of building collapse under blast loads［J］.Engineering Structures，2004，26(1):63-71.

［2］ Hamburger R，Whittaker A.Design of steel structures for blast-related progressive collapse［J］.Modern Steel Construction，2004，44(3):45-51.

［3］ 曹晓中.组合网架在爆炸荷载作用下的设计［J］.建筑结构，2000，30(4):55-57.CAO Xiao-zhong.Design of build-up space grid under action of explosive load［J］.Building Structure，2000，30(4):55-57.

［4］ ZHANG Xiu-hua，DUAN Zhong-dong，ZHANG Chun-wei.Numerical simulation of dynamic response and collapse for steel frame structures subjected to blast load［J］.Transactions of Tianjin University，2008，14:523-529.

［5］ 李忠献，刘志侠，丁阳.爆炸荷载作用下钢结构的动力响应与破坏模式［J］.建筑结构学报，2008，29(4):106-111.LI Zhong-xian，LIU Zhi-xia，DING Yang.Dynamic response and failure modes of steel structures under blast loading［J］.Journal of Building Structure，2008，29(4):106-111.

［6］ Liew J Y Richard.Survivability of steel frame structures subject to blast and fire［J］.Journal of Constructional Steel Research，2008，64(7/8):854-866.

［7］ Liew J Y Richard，CHEN Hong.Explosion and fire analysis of steel frames using fiber element approach［J］.Journal of Structural Engineering，2004，130(7):991-1000.

［8］ 高轩能，王书鹏，江媛.爆炸荷载下大空间结构的冲击波压力场分布及泄爆措施研究［J］.工程力学，2010，27(4):226-233.GAO Xuan-neng，WANG Shu-peng，JIANG Yuan.Shock wave pressure distribution on large space structures and explosion venting under loading［J］.Engineering Mechanics，2010，27(4):226-233.

［9］ LS-DYNA Keyword User’s Manual［Z］.Livermore Software Technology Corporation，2003.

［10］ Razaqpura A G，Tolbab A，Contestabilec E.Blast loading response of reinforced concrete panels reinforced with externally bonded GFRP laminates［J］.Composite Part B:Engineering，2007，38(5/6):535-546.

［11］ Wu C，Hao H.Modeling of simultaneous ground shock and air blast pressure on nearby structures from surface explosions［J］.International Journal of Impact Engineering，2005，31(6):699-717.

［12］ 王永辉.K8 型单层球面网壳在爆炸荷载下的数值模拟［D］.哈尔滨:哈尔滨工业大学，2010.

［13］ FAN Feng，WANG Duo-zhi，ZHI Xu-dong，et al.Failure modes for single-layer reticulated domes under impact loads［J］.Transactions of Tianjin University，2008，14 suppl:545-550.